Lấy ngẫu nhiên 1 thẻ từ một hộp chứa 20 thẻ, được đánh số từ 1 đến 20. Tìm xác suất để thẻ được lấy ra là số
- Chẵn
- Chia hết cho 3
- Lẻ và chia hết cho 3
Trong các mệnh đề sau, mệnh đề nào có mệnh đề đảo đúng?
| Nếu số nguyên \(n\) có tổng các chữ số bằng \(9\) thì \(n\) chia hết cho \(3\) | |
| Nếu \(x>y\) thì \(x^2>y^2\) | |
| Nếu \(x=y\) thì \(t\cdot x=t\cdot y\) | |
| Nếu \(x>y\) thì \(x^3>y^3\) |
Trong các câu sau, câu nào là mệnh đề đúng?
| Nếu \(a\geq b\) thì \(a^2\geq b^2\) | |
| Nếu \(a\) chia hết cho \(9\) thì \(a\) chia hết cho \(3\) | |
| Nếu em chăm chỉ thì em thành công | |
| Nếu một tam giác có một góc bằng \(60^\circ\) thì tam giác đó đều |
Gieo một con súc sắc cân đối và đồng chất. Tính xác suất để xuất hiện mặt có số chấm chia hết cho \(3\).
| \(1\) | |
| \(3\) | |
| \(\dfrac{2}{3}\) | |
| \(\dfrac{1}{3}\) |
Gọi \(A\) là tập hợp các số tự nhiên có \(8\) chữ số đôi một khác nhau. Chọn ngẫu nhiên một số thuộc \(A\). Tính xác suất để số tự nhiên được chọn chia hết cho \(25\).
| \(\dfrac{17}{81}\) | |
| \(\dfrac{43}{324}\) | |
| \(\dfrac{1}{27}\) | |
| \(\dfrac{11}{324}\) |
Trên tập số phức, xét phương trình $z^2+az+b=0$ $(a,b\in\mathbb{R})$. Có bao nhiêu cặp số $(a,b)$ để phương trình đó có hai nghiệm phân biệt $z_1,\,z_2$ thỏa mãn $\big|z_1-2\big|=2$ và $\big|z_2+1-4i\big|=4$?
| $2$ | |
| $3$ | |
| $6$ | |
| $4$ |
Gọi $S$ là tập hợp các số phức $z=a+bi$ $(a,b\in\mathbb{R}$ thỏa mãn $\big|z+\overline{z}\big|+\big|z-\overline{z}\big|=6$ và $ab\le0$. Xét $z_1$ và $z_2$ thuộc $S$ sao cho $\dfrac{z_1-z_2}{-1+i}$ là số thực dương. Giá trị nhỏ nhất của biểu thức $\big|z_1+3i\big|+\big|z_2\big|$ bằng
| $3\sqrt{2}$ | |
| $3$ | |
| $3\sqrt{5}$ | |
| $3+3\sqrt{2}$ |
Gọi $z_1,\,z_2$ là hai nghiệm phức của phương trình $z^2-6z+14=0$ và $M,\,N$ lần lượt là điểm biểu diễn của $z_1,\,z_2$ trên mặt phẳng tọa độ. Trung điểm của đoạn $MN$ có tọa độ là
| $(3;7)$ | |
| $(-3;0)$ | |
| $(3;0)$ | |
| $(-3;7)$ |
Cho số phức $z=1-2i$. Phần ảo của số phức $\overline{z}$ bằng
| $-1$ | |
| $2$ | |
| $1$ | |
| $-2$ |
Cho hai số phức $z_1=2-i$ và $z_2=1+3i$. Phần thực của số phức $z_1-z_2$ bằng
| $3$ | |
| $-4$ | |
| $1$ | |
| $-1$ |
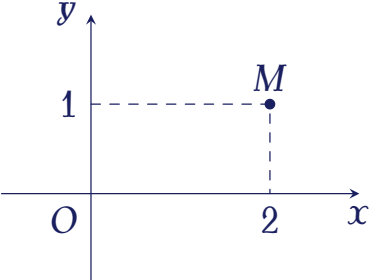
Điểm $M$ trong hình bên là điểm biểu diễn của số phức nào dưới đây?
| $2-i$ | |
| $1+2i$ | |
| $1-2i$ | |
| $2+i$ |
Xét các số phức $z$ thỏa mãn điều kiện $\left|\dfrac{-2-3i}{3-2i}z+1\right|=1$. Gọi $m, M$ lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của biểu thức $P=|z|$. Tính $S=2023-3M+2m$.
| $S=2021$ | |
| $S=2017$ | |
| $S=2019$ | |
| $S=2023$ |
Trong tập hợp số phức, xét phương trình $z^3-(2m+1)z^2+3mz-m=0$ ($m$ là tham số thực). Có bao nhiêu giá trị của $m$ để phương trình đó có ba nghiệm phân biệt $z_1$, $z_2$, $z_3$ thỏa mãn $\big|z_1\big|+\big|z_2\big|+\big|z_3\big|=3$?
| $0$ | |
| $1$ | |
| $2$ | |
| $3$ |
Liên hợp của số phức $z=-1+2i$ là
| $\overline{z}=1-2i$ | |
| $\overline{z}=2-i$ | |
| $\overline{z}=1+2i$ | |
| $\overline{z}=-1-2i$ |
Cho hai số phức $z_1=3-i$ và $z_2=-2+5i$. Khi đó mô-đun của số phức $z=z_1+z_2$ bằng
| $\sqrt{17}$ | |
| $2\sqrt{17}$ | |
| $\sqrt{39}$ | |
| $\sqrt{10}$ |
Trên mặt phẳng tọa độ, điểm biểu diễn số phức $z=2+3i$ có tọa độ là
| $M(-2;3)$ | |
| $M(3;2)$ | |
| $M(2;-3)$ | |
| $M(2;3)$ |
Phần thực của số phức $z=4-6i$ là
| $-4$ | |
| $4$ | |
| $-6$ | |
| $6$ |
Xét số phức $z$ thỏa mãn $|z+3-2i|+|z-3+i|=3\sqrt{5}$. Gọi $M,\,m$ lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức $P=|z+2|+|z-1-3i|$. Khi đó
| $M=\sqrt{26}+2\sqrt{5}$, $m=3\sqrt{2}$ | |
| $M=\sqrt{17}+\sqrt{5}$, $m=\sqrt{2}$ | |
| $M=\sqrt{26}+2\sqrt{5}$, $m=\sqrt{2}$ | |
| $M=\sqrt{17}+\sqrt{5}$, $m=3\sqrt{2}$ |
Cho số phức $z=a+bi$ ($a,\,b\in\mathbb{R}$) thỏa mãn $z-4=(1+i)|z|-(4+3z)i$. Giá trị của biểu thức $P=a-3b$ bằng
| $P=-2$ | |
| $P=6$ | |
| $P=2$ | |
| $P=-6$ |
Biết số phức $z$ thỏa mãn $\big|\overline{z}-3-2i\big|=\sqrt{5}$ và tập hợp các điểm biểu diễn số phức $w=(1-i)z+2$ là một đường tròn. Xác định tâm $I$ và bán kính của đường tròn đó.
| $I(-3;-5)$, $R=\sqrt{5}$ | |
| $I(3;-5)$, $R=\sqrt{10}$ | |
| $I(-3;5)$, $R=\sqrt{10}$ | |
| $I(3;5)$, $R=10$ |
