Cho hàm số $f(x)$ liên tục trên $\mathbb{R}$ thỏa $\displaystyle\displaystyle\int\limits_{0}^{6}f(x)\mathrm{\,d}x=7$, $\displaystyle\displaystyle\int\limits_{3}^{10}f(x)\mathrm{\,d}x=8$, $\displaystyle\displaystyle\int\limits_{3}^{6}f(x)\mathrm{\,d}x=9$. Giá trị của $I=\displaystyle\displaystyle\int\limits_{0}^{10}f(x)\mathrm{\,d}x$ bằng
| $8$ | |
| $6$ | |
| $7$ | |
| $5$ |
Cho hàm số \(f(x)\) liên tục trên đoạn \([0;10]\) thỏa mãn \(\displaystyle\int\limits_{0}^{10}f(x)\mathrm{\,d}x=7\) và \(\displaystyle\int\limits_{2}^{6}f(x)\mathrm{\,d}x=3\). Tính \(P=\displaystyle\int\limits_{0}^{2}f(x)\mathrm{\,d}x+\displaystyle\int\limits_{6}^{10}f(x)\mathrm{\,d}x\).
| \(P=4\) | |
| \(P=10\) | |
| \(P=-6\) | |
| \(P=7\) |
Cho hàm số \(y=f(x)\) liên tục trên \([0;10]\), thỏa mãn \(\displaystyle\int\limits_{0}^{10}f(x)\mathrm{\,d}x=7\) và \(\displaystyle\int\limits_{2}^{6} f(x)\mathrm{\,d}x=3\). Tính giá trị biểu thức \(P=\displaystyle\int\limits_{0}^{2}f(x)\mathrm{\,d}x + \displaystyle\int\limits_{6}^{10} f(x)\mathrm{\,d}x\).
| \(P=4\) | |
| \(P=2\) | |
| \(P=3\) | |
| \(P=10\) |
Cho \(f(x)\) là một hàm số liên tục trên \([-2;5]\) và \(\displaystyle\int\limits_{-2}^5f(x)\mathrm{\,d}x=8\), \(\displaystyle\int\limits_1^3f(x)\mathrm{\,d}x=-3\). Tính \(P=\displaystyle\int\limits_{-2}^1f(x)\mathrm{\,d}x+\displaystyle\int\limits_{3}^5f(x)\mathrm{\,d}x\).
| \(P=5\) | |
| \(P=-11\) | |
| \(P=11\) | |
| \(P=-5\) |
Cho hàm số $f(x)$ liên tục trên $\mathbb{R}$ thỏa $\displaystyle\displaystyle\int\limits_{0}^{1}f(x)\mathrm{d}x=2$ và $\displaystyle\displaystyle\int\limits_{0}^2f(3x+1)\mathrm{d}x=6$. Tính $I=\displaystyle\displaystyle\int\limits_{0}^{7}f(x)\mathrm{d}x$.
| $I=20$ | |
| $I=8$ | |
| $I=18$ | |
| $I=16$ |
Nếu $\displaystyle\displaystyle\int\limits_1^2f(x)\mathrm{\,d}x=2$, $\displaystyle\displaystyle\int\limits_1^4f(x)\mathrm{\,d}x=-1$ thì $\displaystyle\displaystyle\int\limits_2^4f(x)\mathrm{\,d}x$ bằng
| $-3$ | |
| $1$ | |
| $-2$ | |
| $3$ |
Cho hàm số $f\left(x\right)$ liên tục trên $\mathbb{R}$ và có $\displaystyle\displaystyle\int\limits_{0}^{1}f\left(x\right)\mathrm{d}x=2$; $\displaystyle\displaystyle\int\limits_{1}^{3}f\left(x\right)\mathrm{d}x=6$. Tính $I=\displaystyle\displaystyle\int\limits_{0}^{3}f\left(x\right)\mathrm{d}x$.
| $I=8$ | |
| $I=12$ | |
| $I=36$ | |
| $I=4$ |
Cho hai hàm số $f(x)$, $g(x)$ liên tục trên đoạn $[a;b]$ và $a< c< b$. Mệnh đề nào dưới đây sai?
| $\displaystyle\displaystyle\int\limits_a^b\left[f(x)+g(x)\right]\mathrm{\,d}x=\displaystyle\displaystyle\int\limits_a^b f(x)\mathrm{\,d}x+\displaystyle\displaystyle\int\limits_a^b g(x)\mathrm{\,d}x$ | |
| $\displaystyle\displaystyle\int\limits_a^b k\cdot f(x)\mathrm{\,d}x= k\displaystyle\displaystyle\int\limits_a^b f(x)\mathrm{\,d}x$ với $k$ là hằng số | |
| $\displaystyle\displaystyle\int\limits_a^b \dfrac{f(x)}{g(x)}\mathrm{\,d}x=\dfrac{\displaystyle\displaystyle\int\limits_a^b f(x)\mathrm{\,d}x}{\displaystyle\displaystyle\int\limits_a^b g(x)\mathrm{\,d}x}$ | |
| $\displaystyle\displaystyle\int\limits_a^b f(x)\mathrm{\,d}x=\displaystyle\displaystyle\int\limits_a^c f(x)\mathrm{\,d}x+\displaystyle\displaystyle\int\limits_c^b f(x)\mathrm{\,d}x$ |
Nếu $\displaystyle\displaystyle\int\limits_{1}^{2}f(x)\mathrm{\,d}x=5$ và $\displaystyle\displaystyle\int\limits_{2}^{3}f(x)\mathrm{\,d}x=-2$ thì $\displaystyle\displaystyle\int\limits_{1}^{3}f(x)\mathrm{\,d}x$ bằng
| $3$ | |
| $7$ | |
| $-10$ | |
| $-7$ |
Cho \(\displaystyle\int\limits_{0}^{1}f(x)\mathrm{\,d}x=-1\), \(\displaystyle\int\limits_{0}^{3}f(x)\mathrm{\,d}x=5\). Tính \(\displaystyle\int\limits_{1}^{3}f(x)\mathrm{\,d}x\).
| \(5\) | |
| \(4\) | |
| \(1\) | |
| \(6\) |
Cho hàm số \(f(x),\,g(x)\) liên tục trên \([a;b]\). Khẳng định nào sau đây sai?
| \(\displaystyle\int\limits_{a}^{b}\left[f(x)+g(x)\right]\mathrm{\,d}x=\displaystyle\int\limits_{a}^{b}f(x)\mathrm{\,d}x+\displaystyle\int\limits_{a}^{b}g(x)\mathrm{\,d}x\) | |
| \(\displaystyle\int\limits_{a}^{b}f(x)\mathrm{\,d}x=\displaystyle\int\limits_{b}^{a}f(x)\mathrm{\,d}x\) | |
| \(\displaystyle\int\limits_{a}^{b}f(x)\mathrm{\,d}x=\displaystyle\int\limits_{a}^{b}f(t)\mathrm{\,d}t\) | |
| \(\displaystyle\int\limits_{a}^{b}f(x)\mathrm{\,d}x=\displaystyle\int\limits_{c}^{b}f(x)\mathrm{\,d}x+\displaystyle\int\limits_{a}^{c}f(x)\mathrm{\,d}x\) |
Cho \(\displaystyle\int\limits_{-1}^2f(x)\mathrm{\,d}x=5\) và \(\displaystyle\int\limits_0^2f(x)\mathrm{\,d}x=2\). Tính \(I=\displaystyle\int\limits_{-1}^0f(x)\mathrm{\,d}x\).
| \(I=7\) | |
| \(I=-3\) | |
| \(I=3\) | |
| \(I=1\) |
Cho hàm số \(f(x)\) liên tục trên đoạn \([a;b]\) và \(a< c< b\). Mệnh đề nào dưới đây sai?
| \(\displaystyle\int\limits_a^b f(x)\mathrm{\,d}x+\displaystyle\int\limits_a^c f(x)\mathrm{\,d}x=\displaystyle\int\limits_b^c f(x)\mathrm{\,d}x\) | |
| \(\displaystyle\int\limits_a^c f(x)\mathrm{\,d}x+\displaystyle\int\limits_c^b f(x)\mathrm{\,d}x=\displaystyle\int\limits_a^b f(x)\mathrm{\,d}x\) | |
| \(\displaystyle\int\limits_a^b f(x)\mathrm{\,d}x=-\displaystyle\int\limits_b^a f(x)\mathrm{\,d}x\) | |
| \(\displaystyle\int\limits_a^b f(x)\mathrm{\,d}x+\displaystyle\int\limits_b^a f(x)\mathrm{\,d}x=0\) |
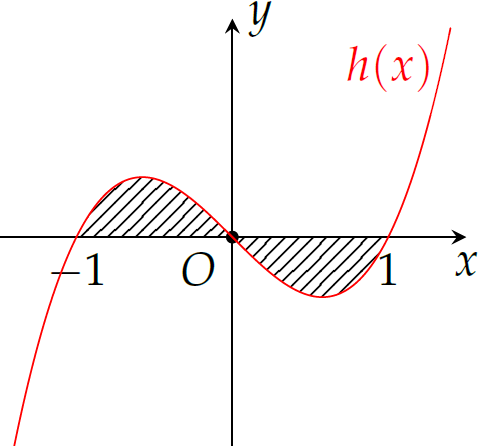
Cho đồ thị hàm số \(y=h(x)\). Diện tích hình phẳng (phần gạch chéo trong hình vẽ) bằng
| \(\displaystyle\int\limits_{-1}^{0}h(x)\mathrm{\,d}x+\displaystyle\int\limits_{0}^{1}h(x)\mathrm{\,d}x\) | |
| \(\displaystyle\int\limits_{-1}^{1}h(x)\mathrm{\,d}x\) | |
| \(\displaystyle\int\limits_{-1}^{0}h(x)\mathrm{\,d}x+\displaystyle\int\limits_{1}^{0}h(x)\mathrm{\,d}x\) | |
| \(-\displaystyle\int\limits_{-1}^{0}h(x)\mathrm{\,d}x+\displaystyle\int\limits_{0}^{1}h(x)\mathrm{\,d}x\) |
Biết \(\displaystyle\int\limits_{1}^{2}f(x)\mathrm{\,d}x=2\) và \(\displaystyle\int\limits_{1}^{3}f(x)\mathrm{\,d}x=3\). Kết quả \(\displaystyle\int\limits_{3}^{2}f(x)\mathrm{\,d}x\) bằng bao nhiêu?
| \(3\) | |
| \(\dfrac{5}{2}\) | |
| \(-1\) | |
| \(1\) |
Với \(a\neq0\). Cho biểu thức \(B=\displaystyle\int\limits_{-1}^{1}ax^2\mathrm{\,d}x\). Khẳng định nào sau đây sai?
| \(B=a\displaystyle\int\limits_{-1}^{1}x^2\mathrm{\,d}x\) | |
| \(B=-\displaystyle\int\limits_{1}^{-1}ax^2\mathrm{\,d}x\) | |
| \(B=\displaystyle\int\limits_{1}^{0}ax^2\mathrm{\,d}x+\displaystyle\int\limits_{0}^{-1}ax^2\mathrm{\,d}x\) | |
| \(B=\dfrac{2a}{3}\) |
Giả sử hàm số \(f\) liên tục trên khoảng \(\mathbb{K}\) và \(a,\,b,\,c\) là \(3\) số thực bất kỳ thuộc \(\mathbb{K}\). Khẳng định nào sau đây sai?
| \(\displaystyle\int\limits_{a}^{b}f(x)\mathrm{\,d}x\neq\displaystyle\int\limits_{a}^{b}f(t)\mathrm{\,d}t\) | |
| \(\displaystyle\int\limits_{a}^{b}f(x)\mathrm{\,d}x=-\displaystyle\int\limits_{b}^{a}f(t)\mathrm{\,d}t\) | |
| \(\displaystyle\int\limits_{a}^{a}f(x)\mathrm{\,d}x=0\) | |
| \(\displaystyle\int\limits_{a}^{b}f(x)\mathrm{\,d}x=\displaystyle\int\limits_{a}^{c}f(x)\mathrm{\,d}x+\displaystyle\int\limits_{c}^{b}f(x)\mathrm{\,d}x\;\left(c\in(a;b)\right)\) |
Tính diện tích \(S\) của hình phẳng giới hạn bởi đồ thị các hàm số \(y=|x|\) và \(y=x^2-2\).
| \(S=\dfrac{20}{3}\) | |
| \(S=\dfrac{11}{2}\) | |
| \(S=3\) | |
| \(S=\dfrac{13}{3}\) |
Cho \(f(x)\) là hàm số chẵn trên \(\mathbb{R}\) thỏa mãn \(\displaystyle\int\limits_{-3}^{0}f(x)\mathrm{\,d}x=2\). Chọn mệnh đề đúng.
| \(\displaystyle\int\limits_{-3}^{3}f(x)\mathrm{\,d}x=4\) | |
| \(\displaystyle\int\limits_{3}^{0}f(x)\mathrm{\,d}x=2\) | |
| \(\displaystyle\int\limits_{0}^{3}f(x)\mathrm{\,d}x=-2\) | |
| \(\displaystyle\int\limits_{-3}^{3}f(x)\mathrm{\,d}x=2\) |
Nếu \(\displaystyle\int\limits_1^2f(x)\mathrm{\,d}x=-2\) và \(\displaystyle\int\limits_2^3f(x)\mathrm{\,d}x=1\) thì \(\displaystyle\int\limits_1^3f(x)\mathrm{\,d}x\) bằng
| \(-3\) | |
| \(-1\) | |
| \(1\) | |
| \(3\) |
