Cho hàm số $$y=2x^3-3(3m+1)x^2+6\left(2m^2+m\right)x-12m^2+3m+1.$$Tính tổng tất cả giá trị nguyên dương của tham số \(m\) để hàm số nghịch biến trên khoảng \((1;3)\).
| \(0\) | |
| \(3\) | |
| \(1\) | |
| \(2\) |
Cho hàm số $f\left(x\right)=x^3-2x^2+mx-3$ . Tìm $m$ để $f'\left(x\right)< 0$ với mọi $x\in\left(0;2\right)$.
Cho hàm số $f\left(x\right)=x^3+ax^2+bx+c$ với $a,\,b,\,c\in\mathbb{R}$. Hãy xác định các số $a,\,b,\,c$ biết rằng $f'\left(\dfrac{1}{3}\right)=0$ và đồ thị của hàm số $y=f\left(x\right)$ đi qua các điểm $\left(-1;-3\right)$ và $\left(1;-1\right)$.
Có bao nhiêu giá trị nguyên của tham số $a\in(-10;+\infty)$ để hàm số $y=\big|x^3+(a+2)x+9-a^2\big|$ đồng biến trên khoảng $(0;1)$?
| $12$ | |
| $11$ | |
| $6$ | |
| $5$ |
Cho hàm số $f(x)$, trong đó $f(x)$ là một đa giác. Hàm số $f'(x)$ có đồ thị như hình vẽ bên.
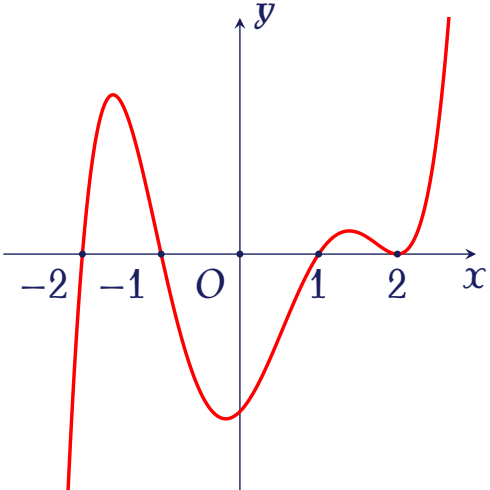
Hỏi có bao nhiêu giá trị nguyên $m$ thuộc $(-5;5)$ để hàm số $y=g(x)=f\big(x^2-2|x|+m\big)$ có $9$ điểm cực trị?
| $3$ | |
| $4$ | |
| $1$ | |
| $2$ |
Tìm giá trị nhỏ nhất của tham số $m$ để bất phương trình $$\dfrac{x^3+\sqrt{3x^2+1}+1}{\sqrt{x}-\sqrt{x-1}}\leq\dfrac{m}{\left(\sqrt{x}+\sqrt{x-1}\right)^2}$$có nghiệm.
| $m=1$ | |
| $m=4$ | |
| $m=13$ | |
| $m=8$ |
Tìm $m$ sao cho bất phương trình $\dfrac{x^2-2x+2}{x-1}\leq m$ có đúng một nghiệm trên khoảng $(1;+\infty)$.
| $m\geq2$ | |
| $m\leq2$ | |
| $m=2$ | |
| $m>2$ |
Tìm tất cả các giá trị thực của tham số $m$ sao cho hàm số $y=\dfrac{mx^3}{3}+7mx^2+14x-m+2$ nghịch biến trên $[1;+\infty)$.
| $\left(-\infty;-\dfrac{14}{15}\right)$ | |
| $\left(-\infty;-\dfrac{14}{15}\right]$ | |
| $\left[-2;-\dfrac{14}{15}\right]$ | |
| $\left[-\dfrac{14}{15};+\infty\right)$ |
Tìm tập hợp giá trị của tham số $m$ để hàm số $y=x^3-mx^2-(m-6)x+1$ đồng biến trên khoảng $(0;4)$.
| $(-\infty;6]$ | |
| $(-\infty;3]$ | |
| $(-\infty;3)$ | |
| $[3;6]$ |
Biết $\left(x^5-3x^4+2019\right)^{\prime}=ax^4+bx^3$. Tìm $S=a+b$.
| $S=-7$ | |
| $S=7$ | |
| $S=17$ | |
| $S=12$ |
Cho hàm số $y=f(x)$ có đạo hàm là $f^{\prime}(x)=12x^2+2$, $\forall x\in\mathbb{R}$ và $f(1)=3$. Biết $F(x)$ là nguyên hàm của $f(x)$ thỏa mãn $F(0)=2$, khi đó $F(1)$ bằng
| $-3$ | |
| $1$ | |
| $2$ | |
| $7$ |
Cho hàm số $f(x)$ thỏa $f(1)=\dfrac{1}{3}$ và $f'(x)=\big[xf(x)\big]^2$ với mọi $x\in\mathbb{R}$. Giá trị $f(2)$ bằng
| $\dfrac{2}{3}$ | |
| $\dfrac{3}{2}$ | |
| $\dfrac{16}{3}$ | |
| $\dfrac{3}{16}$ |
Biết $F(x)=-\dfrac{1}{x^2}$ là một nguyên hàm của hàm số $y=\dfrac{f(x)}{x}$. Tính $\displaystyle\displaystyle\int f'(x)\ln{x}\mathrm{\,d}x$.
| $\displaystyle\displaystyle\int\limits f'(x)\ln{x}\mathrm{\,d}x=-\dfrac{2\ln{x}}{x^2}+\dfrac{1}{x^2}+C$ | |
| $\displaystyle\displaystyle\int\limits f'(x)\ln{x}\mathrm{\,d}x=\dfrac{2\ln{x}}{x^2}+\dfrac{1}{x^2}+C$ | |
| $\displaystyle\displaystyle\int\limits f'(x)\ln{x}\mathrm{\,d}x=\dfrac{2\ln{x}}{x^2}-\dfrac{1}{x^2}+C$ | |
| $\displaystyle\displaystyle\int\limits f'(x)\ln{x}\mathrm{\,d}x=-\dfrac{2\ln{x}}{x^2}-\dfrac{1}{x^2}+C$ |
Biết $\displaystyle\displaystyle\int\left(3x^3+5x^4\right)\mathrm{\,d}x=Ax^\alpha+Bx^\beta+C$. Tính $P=A\alpha+B\beta$.
| $P=37$ | |
| $P=4$ | |
| $P=29$ | |
| $P=8$ |
Cho hàm số $f(x)$ xác định trên $\mathbb{R}\setminus\{1;4\}$ có $f'(x)=\dfrac{2x-5}{x^2-5x+4}$ thỏa mãn $f(3)=1$. Giá trị $f(2)$ bằng
| $1$ | |
| $-1+3\ln2$ | |
| $1+3\ln2$ | |
| $1-\ln2$ |
Cho $\left(\dfrac{2x^2-3x+5}{x-3}\right)^{\prime}=\dfrac{ax^2-bx+c}{\left(x-3\right)^2}$. Tính $S=a+b+c$.
| $S=0$ | |
| $S=12$ | |
| $S=-6$ | |
| $S=18$ |
Cho hàm số $y=\begin{cases}x^2+ax+b&\text{khi }x\ge2\\ x^3-x^2-8x+10&\text{khi }x<2\end{cases}$. Biết hàm số có đạo hàm tại điểm $x=2$. Giá trị của $a^2+b^2$ bằng
| $20$ | |
| $17$ | |
| $18$ | |
| $25$ |
Cho hàm số $f\left(x\right)=\begin{cases}ax^2+bx+1&\text{khi }x\ge0\\ ax-b-1&\text{khi }x<0\end{cases}$. Khi hàm số $f\left(x\right)$ có đạo hàm tại $x_0=0$, hãy tính $T=a+2b$.
| $T=-4$ | |
| $T=0$ | |
| $T=-6$ | |
| $T=4$ |
Đạo hàm của hàm số \(y=\dfrac{-x^2+3x-3}{2(x-1)}\) là biểu thức có dạng \(\dfrac{ax^2+bx}{2(x-1)^2}\). Khi đó, tích \(a\cdot b\) bằng
| \(-1\) | |
| \(6\) | |
| \(4\) | |
| \(-2\) |
Cho biết $$\displaystyle\int\dfrac{2x-13}{(x+1)(x-2)}\mathrm{\,d}x=a\ln|x+1|+b\ln|x-2|+C$$Mệnh đề nào sau đây đúng?
| \(a-b=8\) | |
| \(2a-b=8\) | |
| \(a+2b=8\) | |
| \(a+b=8\) |
