Cho hàm số bậc hai $y=f(x)$ có đồ thị như hình vẽ.
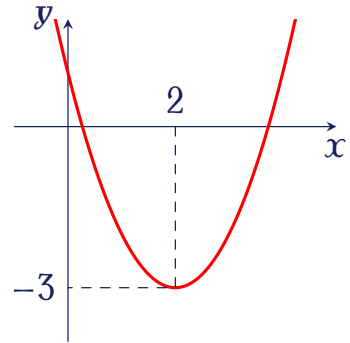
Tìm số nghiệm thực của phương trình $\big|f\big(x^3-2x^2+x\big)\big|=2$.
| $1$ | |
| $3$ | |
| $4$ | |
| $2$ |
Cho hàm số bậc ba $y=f(x)$ có đồ thị như hình vẽ.
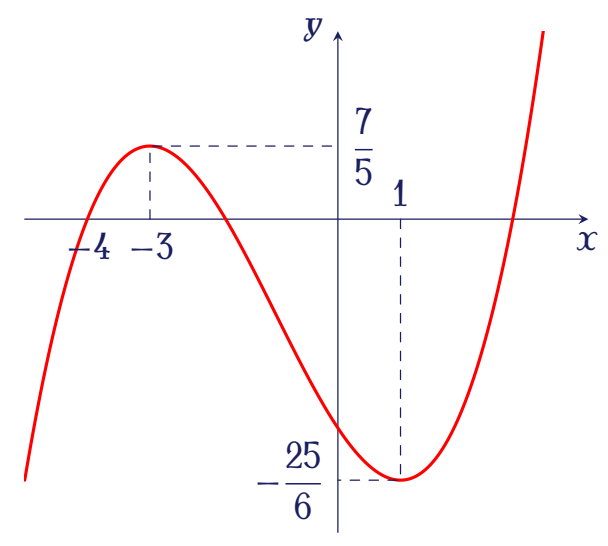
Tìm số nghiệm thực của phương trình $\big|f\big(x^2-4x\big)\big|=\dfrac{3}{4}$.
| $12$ | |
| $6$ | |
| $10$ | |
| $8$ |
Cho hàm số bậc ba $y=f(x)$ có đồ thị như hình vẽ.
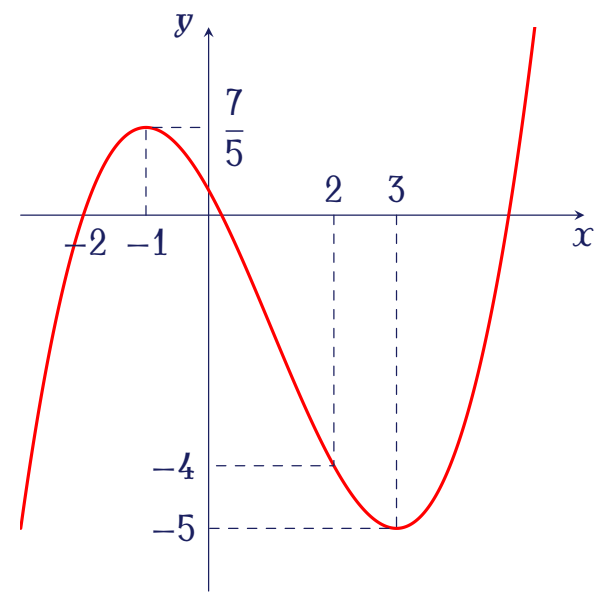
Tìm số nghiệm thực của phương trình $\big|f\big(x^3-3x\big)\big|=2$.
| $12$ | |
| $6$ | |
| $10$ | |
| $8$ |
Cho hàm số bậc bốn $f(x)=ax^4+bx^3+cx^2+dx+e$ có đồ thị như hình vẽ.
Số nghiệm của phương trình $f\big(f(x)\big)+1=0$ là
| $3$ | |
| $5$ | |
| $4$ | |
| $6$ |
Cho hàm số bậc ba \(y=f(x)\) có đồ thị là đường cong trong hình.
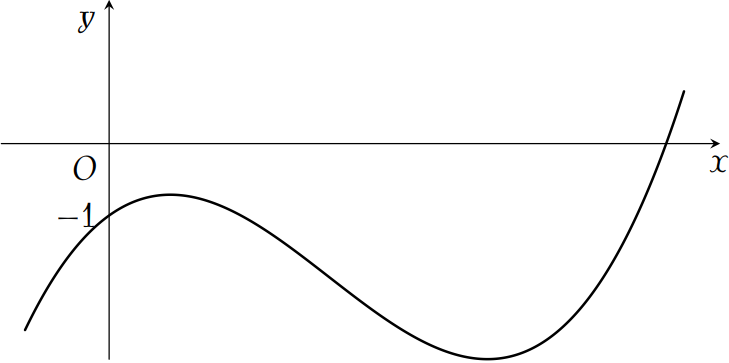
Số nghiệm thực phân biệt của phương trình \(f\left(x^3f(x)\right)+1=0\) là
| \(8\) | |
| \(5\) | |
| \(6\) | |
| \(4\) |
Cho hàm số bậc ba $y=f(x)$ có đồ thị là đường cong trong hình bên.
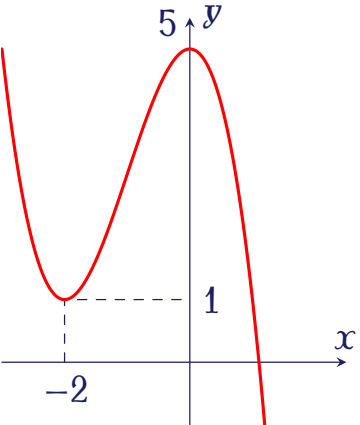
Số nghiệm thực của phương trình $f(x)=2$ là
| $1$ | |
| $0$ | |
| $2$ | |
| $3$ |
Cho hàm số bậc ba $y=f(x)$ có đồ thị là đường cong như hình vẽ bên.
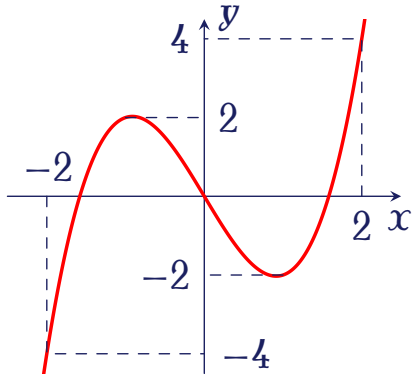
Hỏi phương trình $\big|f(x)-1\big|=1$ có bao nhiêu nghiệm?
| $6$ | |
| $3$ | |
| $4$ | |
| $5$ |
Cho hàm số $f(x)=ax^4+bx^2+c$ có đồ thị là đường cong trong hình bên.
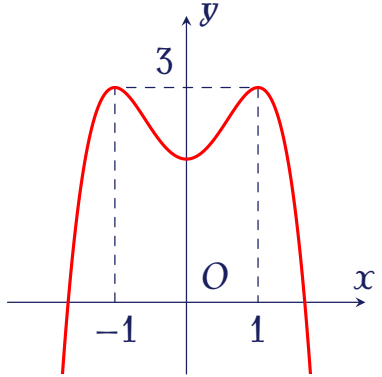
Số nghiệm thực của phương trình $f(x)=1$ là
| $1$ | |
| $2$ | |
| $4$ | |
| $3$ |
Cho hàm số bậc ba $y=f(x)$ có đồ thị là đường cong trong hình bên.
Số nghiệm thực phân biệt của phương trình $f\big(f(x)\big)=1$ là
| $9$ | |
| $3$ | |
| $6$ | |
| $7$ |
Cho hàm số $y=f(x)$ có bảng biến thiên như sau:

Số nghiệm thực phân biệt của phương trình $f'\left(f(x)\right)=0$ là
| $3$ | |
| $4$ | |
| $5$ | |
| $6$ |
Cho hàm số bậc ba \(y=f\left(x\right)\) có đồ thị là đường cong trong hình.

Số nghiệm thực của phương trình \(f\left(x\right)=-1\) là
| \(3\) | |
| \(1\) | |
| \(0\) | |
| \(2\) |
Cho hàm số \(y=\tan x\) có đồ thị như hình vẽ:
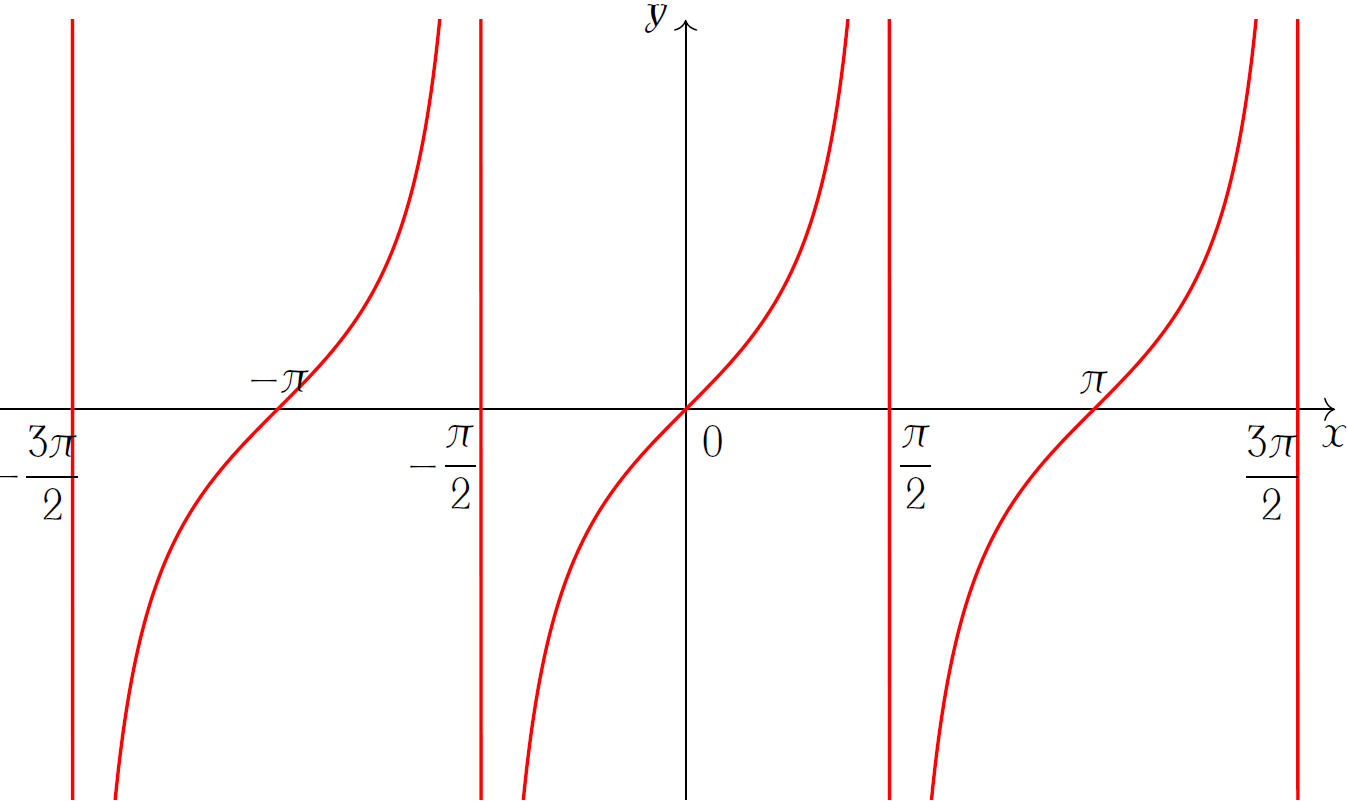
Khẳng định nào sau đây sai?
| Hàm số đồng biến trên \(\left(-\dfrac{\pi}{2};0\right)\) | |
| \(\tan x>0,\forall x\in\left(0;\dfrac{\pi}{2}\right)\) | |
| Đồ thị hàm số luôn cắt trục hoành tại một điểm | |
| Đồ thị hàm số nhận gốc tọa độ \(O\) làm tâm đối xứng nên hàm số \(y=\tan x\) là hàm số lẻ |
Cho đồ thị hàm số \(y=\cos2x\) có đồ thị như hình.
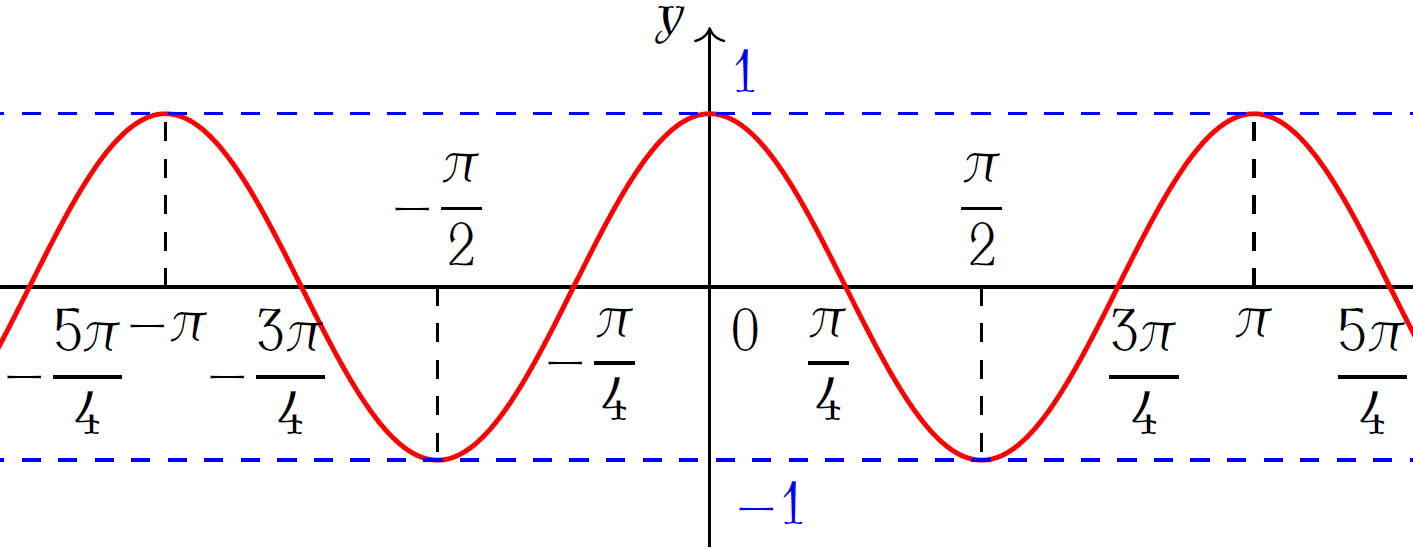
Mệnh đề nào sau đây sai?
| Trên đoạn \(\left[0;\dfrac{\pi}{4}\right]\) hàm số có giá trị lớn nhất bằng \(1\) | |
| Trên đoạn \(\left[0;\dfrac{\pi}{4}\right]\) hàm số có giá trị nhỏ nhất bằng \(-1\) | |
| Trên \(\mathbb{R}\), hàm số có giá trị lớn nhất bằng \(1\) | |
| Trên \(\mathbb{R}\), hàm số có giá trị nhỏ nhất bằng \(-1\) |
Cho hàm số \(f\left(x\right)\) có bảng biến thiên như sau:
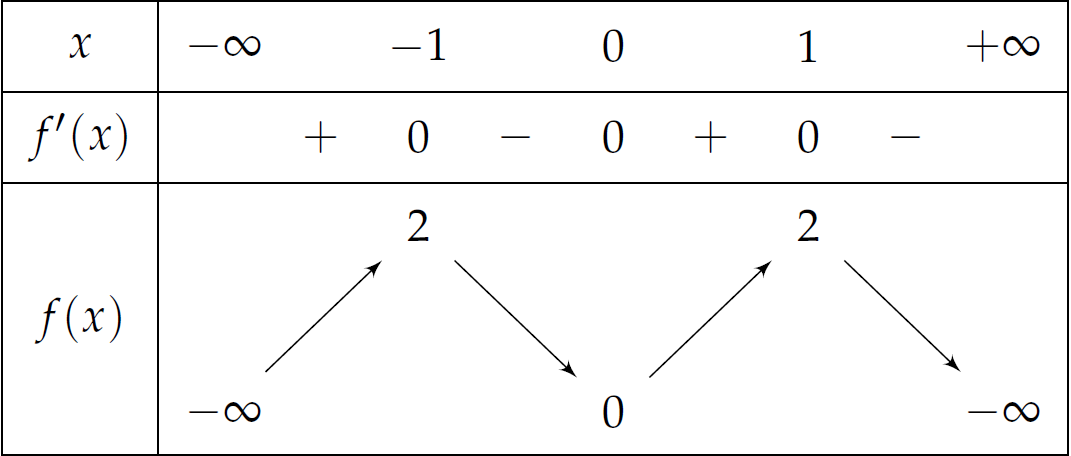
Số nghiệm thuộc đoạn \(\left[0;\dfrac{5\pi}{2}\right]\) của phương trình \(f\left(\sin x\right)=1\) là
| \(7\) | |
| \(4\) | |
| \(5\) | |
| \(6\) |
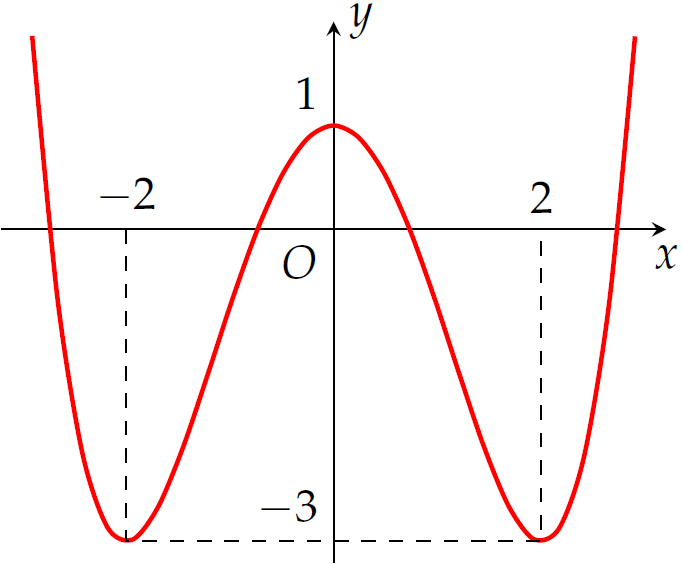
Cho hàm số \(y=f\left(x\right)\) có đồ thị trong hình vẽ trên. Số nghiệm của phương trình \(f\left(x\right)=-1\) là
| \(3\) | |
| \(2\) | |
| \(1\) | |
| \(4\) |
Cho hàm số \(f(x)\) có bảng biến thiên như sau:
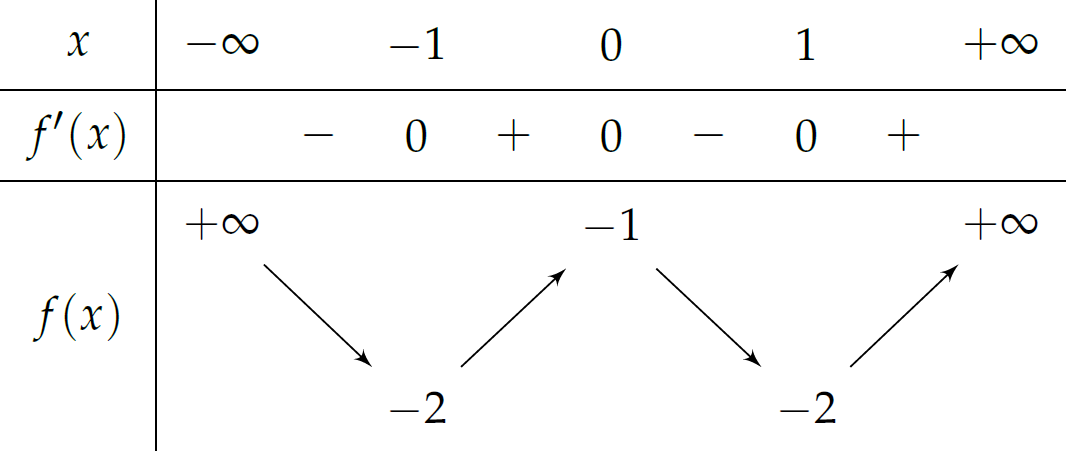
Số nghiệm thuộc đoạn \(\left[-\pi;2\pi\right]\) của phương trình \(2f\left(\sin x\right)+3=0\) là
| \(4\) | |
| \(6\) | |
| \(3\) | |
| \(8\) |
Cho hàm số bậc bốn $y=f(x)$ có đồ thị là đường cong như hình vẽ bên dưới.
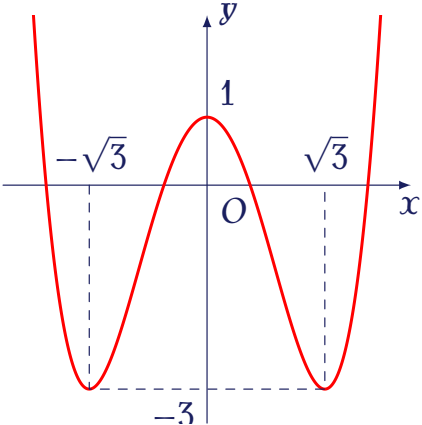
Có bao nhiêu giá trị nguyên âm của tham số $m$ để phương trình $f(x)=m$ có bốn nghiệm thực phân biệt?
| $3$ | |
| $2$ | |
| $4$ | |
| $5$ |
Cho hàm số $y=f(x)$ có đồ thị là đường cong như hình vẽ.
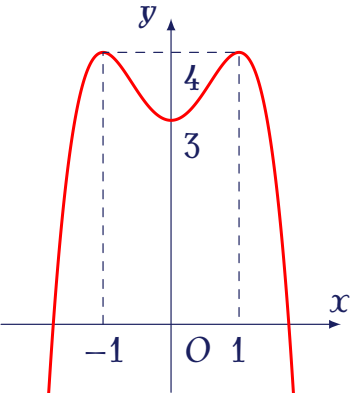
Tọa độ giao điểm của đồ thị đã cho và trục tung là
| $(4;0)$ | |
| $(0;4)$ | |
| $(0;3)$ | |
| $(3;0)$ |
Cho hàm số $f(x)=ax^4+bx^2+c$ ($a\neq0$) có đồ thị là đường cong trong hình bên.
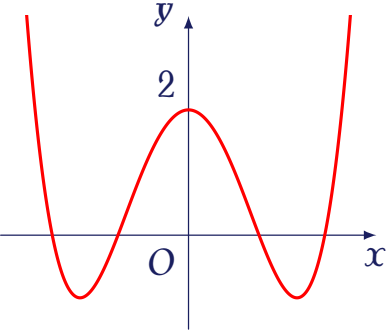
Số nghiệm của phương trình $f(x)-1=0$ là
| $2$ | |
| $1$ | |
| $4$ | |
| $3$ |
Cho hàm số $y=f(x)$ có đồ thị là đường cong trong hình bên.
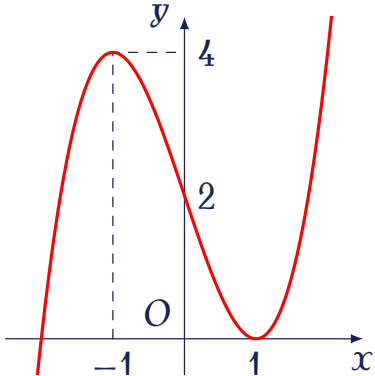
Giá trị của tham số $m$ để phương trình $f(x)+1=m$ có ba nghiệm phân biệt là
| $0< m< 4$ | |
| $1< m< 5$ | |
| $-1< m< 4$ | |
| $0< m< 5$ |
