Cho hình lăng trụ đều $ABC.A'B'C'$ có $AB=a$, $AA'=a\sqrt{3}$. Tính góc tạo bởi đường thẳng $AC'$ và mặt phẳng $(ABC)$.
| $60^\circ$ | |
| $45^\circ$ | |
| $30^\circ$ | |
| $75^\circ$ |
Cho hình lập phương $ABCD.A'B'C'D'$. Tính góc giữa 2 đường thẳng $AC$ và $B'C$.
| $30^\circ$ | |
| $45^\circ$ | |
| $60^\circ$ | |
| $90^\circ$ |
Cho khối lăng trụ đứng $ABC.A'B'C'$ có đáy là tam giác đều cạnh $a$ và $AA'=2a$ (minh họa như hình vẽ bên).
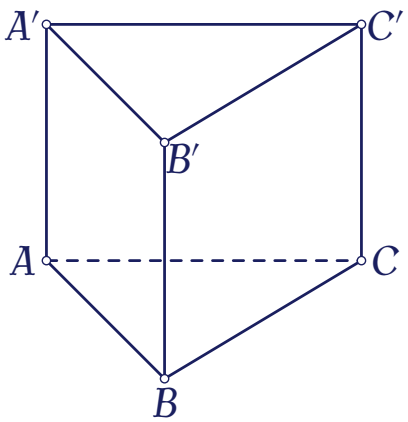
Thể tích của khối lăng trụ đã cho bằng
| $\sqrt{3}a^3$ | |
| $\dfrac{\sqrt{3}a^3}{6}$ | |
| $\dfrac{\sqrt{3}a^3}{3}$ | |
| $\dfrac{\sqrt{3}a^3}{2}$ |
Cho hình lăng trụ đều $ABC.A'B'C'$ có $AB=a$, $AA'=a\sqrt{3}$. Tính góc tạo bởi đường thẳng $AC'$ và mặt phẳng $(ABC)$.
| $60^\circ$ | |
| $45^\circ$ | |
| $30^\circ$ | |
| $75^\circ$ |
Cho hình lăng trụ đứng $ABC.A'B'C'$ có đáy $ABC$ là tam giác vuông tại $B$, $AC=2$, $AB=\sqrt{3}$ và $AA'=1$ (tham khảo hình bên).
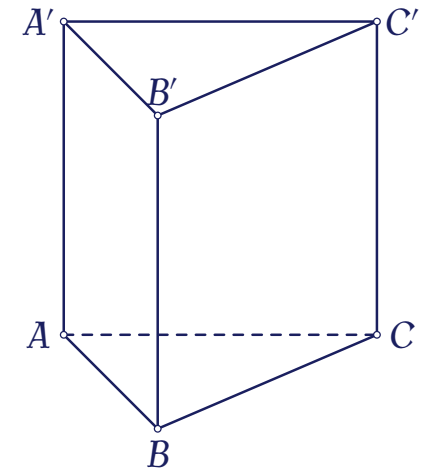
Góc giữa hai mặt phẳng $(ABC')$ và $(ABC)$ bằng
| $30^\circ$ | |
| $45^\circ$ | |
| $90^\circ$ | |
| $60^\circ$ |
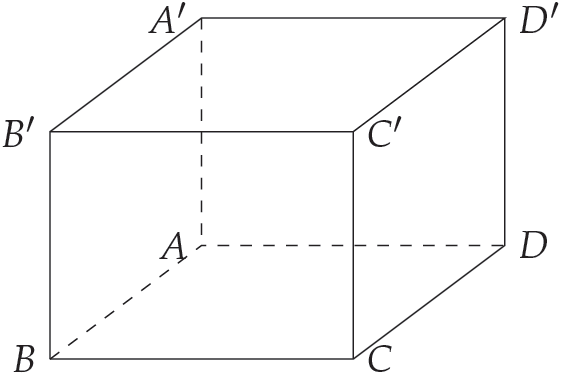
Cho hình lăng trụ đứng \(ABCD.A'B'C'D'\) có đáy là hình thoi cạnh \(a\), \(BD=a\sqrt{3}\), \(AA'=4a\) (minh họa như hình trên). Thể tích của khối lăng trụ đã cho bằng
| \(2\sqrt{3}a^3\) | |
| \(4\sqrt{3}a^3\) | |
| \(\dfrac{2\sqrt{3}a^3}{3}\) | |
| \(\dfrac{4\sqrt{3}a^3}{3}\) |
Cho hình lăng trụ tam giác đều $ABC.A'B'C'$ có $AB=a$, $AA'=2a$. Một khối trụ có hai đáy là hai đường tròn ngoại tiếp hai tam giác $ABC.A'B'C'$. Thể tích của khối trụ đó bằng
| $\dfrac{4\pi a^3}{3}$ | |
| $\pi a^3$ | |
| $\dfrac{2\pi a^3}{3}$ | |
| $\dfrac{\pi a^3}{3}$ |
Cho khối lăng trụ đứng $ABC.A'B'C'$ có đáy $ABC$ là tam giác vuông cân tại $A$, $AB=2a$. Góc giữa đường thẳng $BC'$ và mặt phẳng $(ACC'A')$ bằng $30^\circ$. Thể tích của khối lăng trụ đã cho bằng
| $3a^3$ | |
| $a^3$ | |
| $12\sqrt{2}a^3$ | |
| $4\sqrt{2}a^3$ |
Cho lăng trụ đứng $ABC.A'B'C'$ có tất cả các cạnh bằng nhau và bằng $a$ (tham khảo hình bên).
Khoảng cách từ điểm $A$ đến mặt phẳng $(BCC'B')$ bằng
| $\dfrac{a\sqrt{3}}{4}$ | |
| $a$ | |
| $\dfrac{a\sqrt{3}}{2}$ | |
| $a\sqrt{3}$ |
Cho khối hộp chữ nhật $ABCD.A'B'C'D'$ có đáy hình vuông. $BD=2a$, góc giữa hai mặt phẳng $\left(A'BD\right)$ và $(ABCD)$ bằng $30^\circ$. Thể tích của khối hộp chữ nhật đã cho bằng
| $6\sqrt{3}a^3$ | |
| $\dfrac{2\sqrt{3}}{9}a^3$ | |
| $2\sqrt{3}a^3$ | |
| $\dfrac{2\sqrt{3}}{3}a^3$ |
Cho hình lăng trụ đứng $ABC.A'B'C'$ có đáy $ABC$ là tam giác vuông cân tại $B$ và $AB=4$ (tham khảo hình bên).
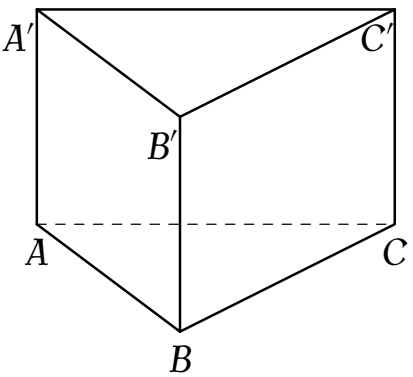
Khoảng cách từ $C$ đến mặt phẳng $\left(ABB'A'\right)$ bằng
| $2\sqrt{2}$ | |
| $2$ | |
| $\sqrt{2}$ | |
| $4$ |
Cho hình hộp $ABCD.A'B'C'D'$ có tất cả các cạnh bằng nhau (tham khảo hình bên).
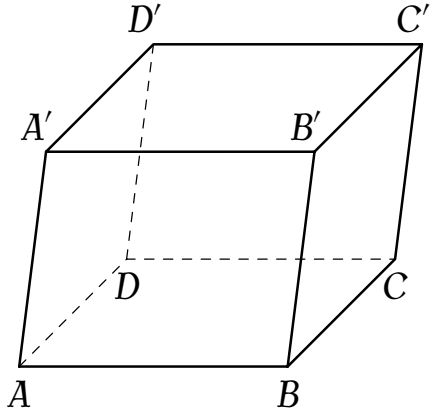
Góc giữa hai đường thẳng $A'C'$ và $BD$ bằng
| $90^{\circ}$ | |
| $30^{\circ}$ | |
| $45^{\circ}$ | |
| $60^{\circ}$ |
Hình lăng trụ đứng tam giác có bao nhiêu mặt là hình chữ nhật?
| $3$ | |
| $1$ | |
| $5$ | |
| $2$ |
Cho hình hộp chữ nhật $ABCD.A'B'C'D'$ có $AB=AD=2$ và $AA'=2\sqrt{2}$ (tham khảo hình bên).
Góc giữa đường thẳng $CA'$ và mặt phẳng $(ABCD)$ bằng
| $30^\circ$ | |
| $45^\circ$ | |
| $60^\circ$ | |
| $90^\circ$ |
Các kích thước của một bể bơi được cho trên hình vẽ (mặt nước có dạng hình chữ nhật).
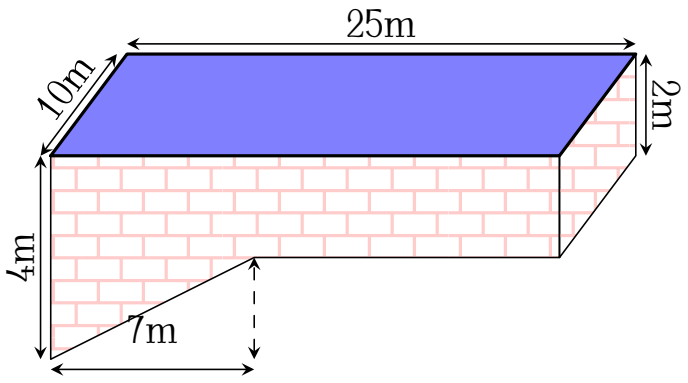
Hãy tính xem bể bơi chứa được bao nhiêu mét khối nước khi nó đầy ắp nước?
| $1000$m$^3$ | |
| $640$m$^3$ | |
| $570$m$^3$ | |
| $500$m$^3$ |
Tính thể tích của khối gỗ có hình dạng dưới đây
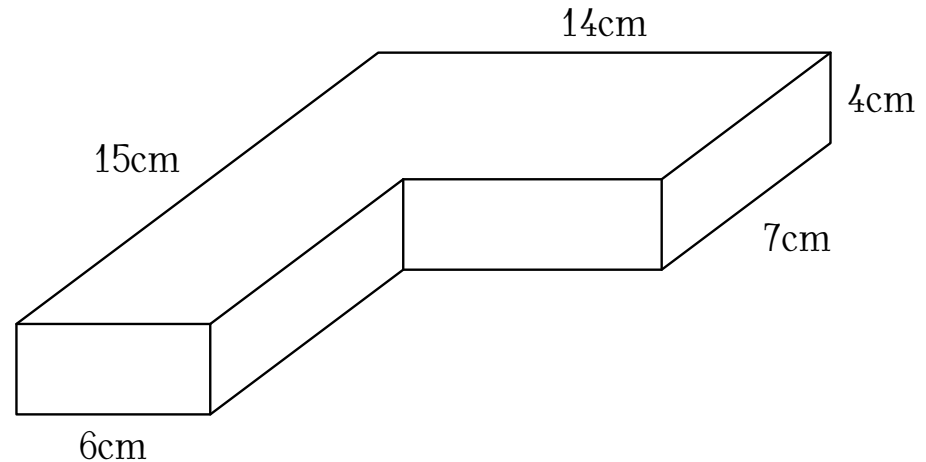
| $328$cm$^3$ | |
| $456$cm$^3$ | |
| $584$cm$^3$ | |
| $712$cm$^3$ |
Cho khối lăng trụ tam giác đều có tất cả các cạnh bằng nhau và thể tích của khối lăng trụ bằng $2\sqrt{3}$. Tính cạnh của khối lăng trụ.
| $6$ | |
| $4$ | |
| $3$ | |
| $2$ |
Đường thẳng nào sau đây không phải đường cao của lăng trụ đều $ABC.A'B'C'$?
| $AA'$ | |
| $BB'$ | |
| $AB'$ | |
| $CC'$ |
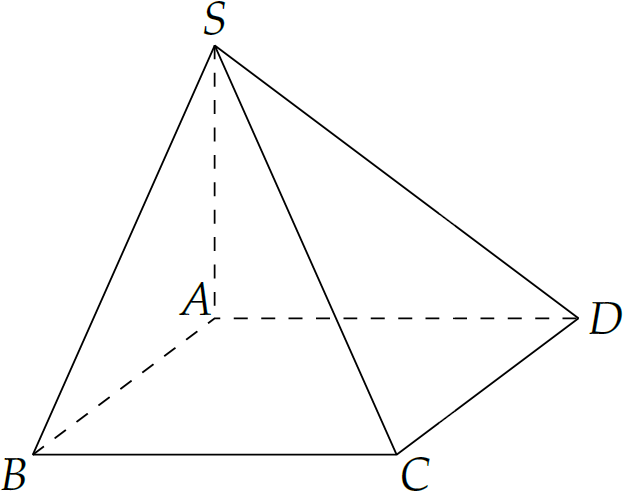
Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh \(a\sqrt{3}\), \(SA\) vuông góc với mặt phẳng đáy và \(SA=a\sqrt{2}\) (như hình minh họa trên). Góc giữa đường thẳng \(SC\) và mặt phẳng \((ABCD)\) bằng
| \(45^\circ\) | |
| \(30^\circ\) | |
| \(60^\circ\) | |
| \(90^\circ\) |
Cho hình lăng trụ tam giác đều $ABC.A'B'C'$ có $AB=a$, $AA'=2a$. Một khối trụ có hai đáy là hai đường tròn ngoại tiếp hai tam giác $ABC$, $A'B'C'$. Thể tích của khối trụ đó bằng
| $\dfrac{4\pi a^3}{3}$ | |
| $\pi a^3$ | |
| $\dfrac{2\pi a^3}{3}$ | |
| $\dfrac{\pi a^3}{3}$ |
