Hàm số nào sau đây đồng biến trên \(\mathbb{R}\)?
| \(y=\dfrac{x-1}{x+1}\) | |
| \(y=\log_2x\) | |
| \(y=3^x\) | |
| \(y=x^4+2x^2+4\) |
Trong các hàm số dưới đây, hàm số nào nghịch biến trên \(\mathbb{R}\)?
| \(y=\left(\dfrac{\pi}{3}\right)^x\) | |
| \(y=\log_{\tfrac{\pi}{4}}\left(2x^2+1\right)\) | |
| \(y=\left(\dfrac{2}{\mathrm{e}}\right)^x\) | |
| \(y=\log_{\tfrac{2}{3}}x\) |
Hàm số nào sau đây đồng biến trên \(\mathbb{R}\)?
| \(y=\log_2x\) | |
| \(y=\dfrac{x-1}{x+1}\) | |
| \(y=3^x\) | |
| \(y=x^4+2x^2+4\) |
Hàm số nào sau đây nghịch biến trên tập xác định của nó?
| \(y=\log_{\tfrac{\pi}{4}}x\) | |
| \(y=\log_\pi x\) | |
| \(y=\left(\dfrac{\sqrt{5}}{2}\right)^x\) | |
| \(y=2^x\) |
Hàm số nào dưới đây nghịch biến trên $\mathbb{R}$?
| $y=\mathrm{e}^x$ | |
| $y=\big(\sqrt{2}\big)^x$ | |
| $y=\left(\dfrac{4}{3}\right)^x$ | |
| $y=\left(\dfrac{1}{3}\right)^x$ |
Hàm số nào dưới đây nghịch biến trên $\mathbb{R}$?
| $y=\mathrm{e}^x$ | |
| $y=\big(\sqrt{2}\big)^x$ | |
| $y=\left(\dfrac{4}{3}\right)^x$ | |
| $y=\left(\dfrac{1}{3}\right)^x$ |
Hàm số nào sau đây nghịch biến trên \(\mathbb{R}\)?
| \(y=2019^x\) | |
| \(y=3^{-x}\) | |
| \(y=\left(\sqrt{\pi}\right)^x\) | |
| \(y=\mathrm{e}^x\) |
Hàm số nào sau đây nghịch biến trên tập xác định của nó?
| \(y=\left(\dfrac{\mathrm{e}}{2}\right)^{-2x}\) | |
| \(y=\left(\dfrac{3}{\mathrm{e}}\right)^x\) | |
| \(y=\left(\dfrac{1}{3}\right)^{-x}\) | |
| \(y=2019^x\) |
Tiệm cận ngang của đồ thị hàm số $y=3^x$ và tiệm cận đứng của đồ thị hàm số $y=\log_2x$ lần lượt có phương trình là
| $y=3$ và $x=0$ | |
| $x=0$ và $y=0$ | |
| $y=0$ và $x=2$ | |
| $y=0$ và $x=0$ |
Cho các hàm số \(y=\log_ax\), \(y=b^x\), \(y=c^x\) có đồ thị như hình vẽ.
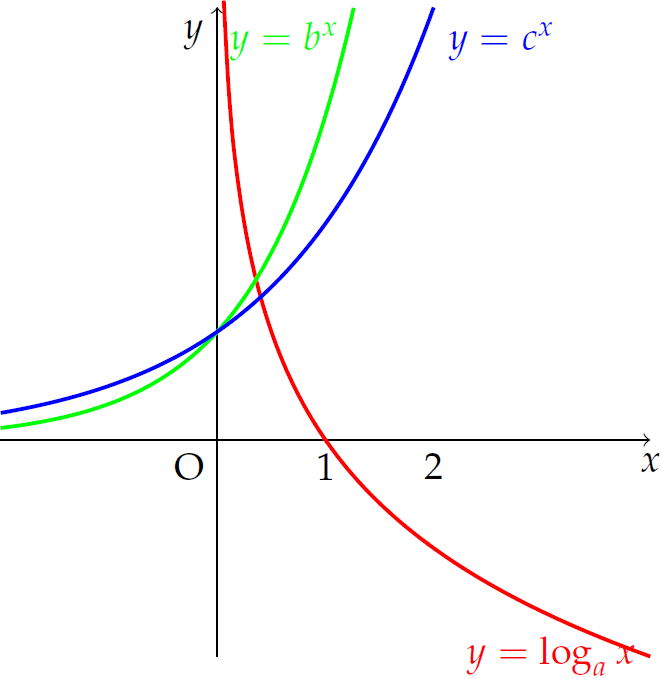
Mệnh đề nào dưới đây là đúng?
| \(b>c>a\) | |
| \(a>b>c\) | |
| \(b>a>c\) | |
| \(c>b>a\) |
Hình vẽ bên biểu diễn đồ thị của hai hàm số \(y=a^x\) và \(y=\log_bx\) với \(a,\,b\) là các số thực dương và \(b\neq1\).
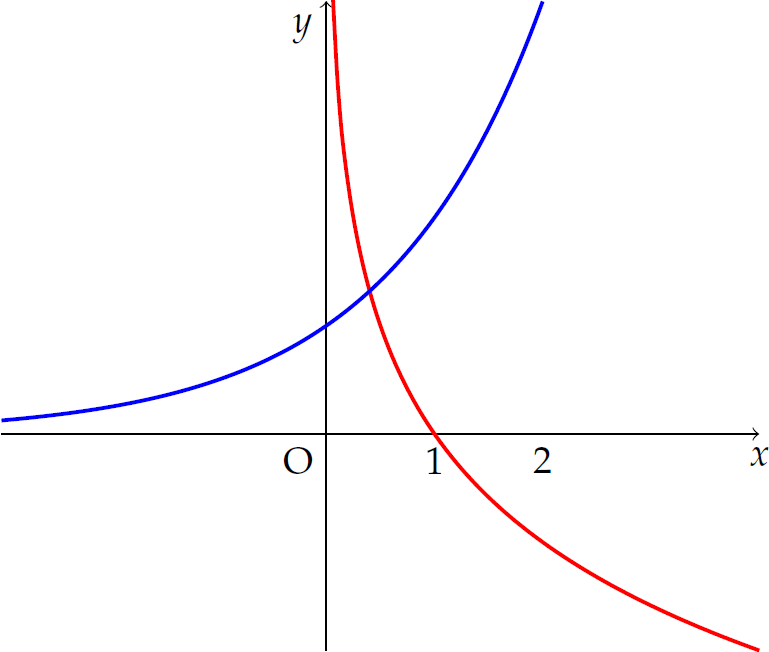
Mệnh đề nào dưới đây là đúng?
| \(\log_ab^2>0\) | |
| \(\log_ab<0\) | |
| \(\log_ab>0\) | |
| \(\log_ba>0\) |
Tìm các khoảng đồng biến của hàm số $$y=2^{x^2-6x+5}$$
| \((-\infty;3)\) | |
| \(\mathbb{R}\) | |
| \((3;+\infty)\) | |
| \((-\infty;1)\) và \((5;+\infty)\) |
Tìm đạo hàm của hàm số \(y=2^x\ln x-\dfrac{1}{\mathrm{e}^x}\).
| \(y'=2^x\left(\dfrac{1}{x}+\ln2\cdot\ln x\right)+\dfrac{1}{\mathrm{e}^x}\) | |
| \(y'=2^x\ln2+\dfrac{1}{x}+\mathrm{e}^{-x}\) | |
| \(y'=\dfrac{2^x}{x}\ln2+\dfrac{1}{\mathrm{e}^x}\) | |
| \(y'=2^x\ln2+\dfrac{1}{x}-\mathrm{e}^{-x}\) |
Tìm đạo hàm của hàm số \(y=\ln\left(1+\mathrm{e}^{2x}\right)\).
| \(y'=\dfrac{-2\mathrm{e}^{2x}}{\left(1+\mathrm{e}^{2x}\right)^2}\) | |
| \(y'=\dfrac{\mathrm{e}^{2x}}{1+\mathrm{e}^{2x}}\) | |
| \(y'=\dfrac{1}{1+\mathrm{e}^{2x}}\) | |
| \(y'=\dfrac{2\mathrm{e}^{2x}}{1+\mathrm{e}^{2x}}\) |
Tập hợp các giá trị thực của tham số \(m\) để phương trình \(\log_2x=m\) có nghiệm là
| \((0;+\infty)\) | |
| \([0;+\infty)\) | |
| \((-\infty;0)\) | |
| \(\mathbb{R}\) |
Cho hàm số \(y=\log_2x\). Khẳng định nào sau đây sai?
| Đồ thị hàm số nhận trục tung làm tiệm cận đứng | |
| Đồ thị hàm số cắt trục hoành tại điểm \(A(1;0)\) | |
| Đồ thị hàm số luôn nằm phía trên trục hoành | |
| Hàm số đồng biến trên khoảng \((0;+\infty)\) |
Cho hàm số \(y=\log_{2019}x\) có đồ thị \((\mathscr{C})\). Mệnh đề nào sau đây sai?
| \((\mathscr{C})\) có đúng một tiệm cận | |
| \((\mathscr{C})\) không có tiệm cận ngang | |
| \((\mathscr{C})\) đồng biến trên tập xác định | |
| \((\mathscr{C})\) không có tiệm cận đứng |
Có tât cả bao nhiêu giá trị nguyên của tham số $m$ để hàm số $y=\dfrac{1}{3}x^3-mx^2+9x-1$ đồng biến trên $\mathbb{R}$?
| $8$ | |
| $9$ | |
| $7$ | |
| $6$ |
Hàm số nào dưới đây nghịch biến trên tập $\mathbb{R}$?
| $y=3x^3-x$ | |
| $y=-2x^4-x$ | |
| $y=-2x^3+3$ | |
| $y=-x^4+2$ |
Số giá trị nguyên của tham số $m$ để hàm số $y=x^3-(m+1)x^2+3x+1$ đồng biến trên $\mathbb{R}$ là
| $4$ | |
| $6$ | |
| $5$ | |
| $7$ |
