Cho hàm số bậc hai $y=f(x)$ có đồ thị $(P)$ và đường thẳng $d$ cắt $(P)$ tại hai điểm như trong hình vẽ bên.
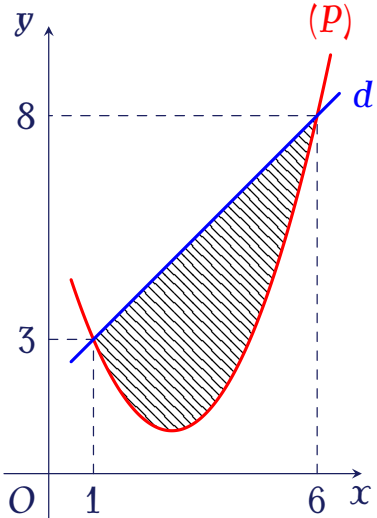
Biết rằng hình phẳng giới hạn bởi $(P)$ và $d$ có diện tích $S=\dfrac{125}{9}$. Tích phân $\displaystyle\displaystyle\int\limits_1^6(2x-5)f'(x)\mathrm{~d}x$ bằng
| $\dfrac{830}{9}$ | |
| $\dfrac{178}{9}$ | |
| $\dfrac{340}{9}$ | |
| $\dfrac{925}{18}$ |
Đường gấp khúc $ABC$ trong hình vẽ bên là đồ thị của hàm số $y=f(x)$ trên đoạn $[-2;3]$.
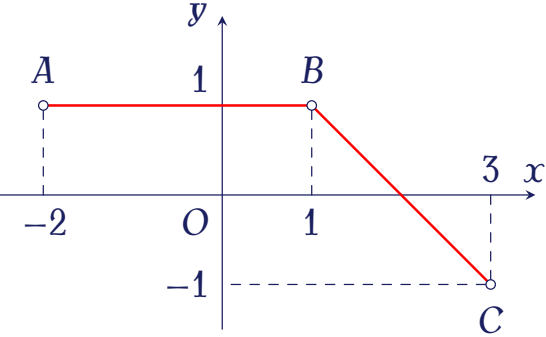
Tích phân $\displaystyle\displaystyle\int\limits_{-2}^3f(x)\mathrm{~d}x$ bằng
| $4$ | |
| $\dfrac{9}{2}$ | |
| $\dfrac{7}{2}$ | |
| $3$ |
Cho hai hàm số $f(x)=mx^3+nx^2+px-\dfrac{5}{2}$ $(m,\,n,\,p\in\mathbb{R})$ và $g(x)=x^2+2x-1$ có đồ thị cắt nhau tại ba điểm có hoành độ lần lượt là $-3$, $-1$, $1$ (tham khảo hình vẽ).
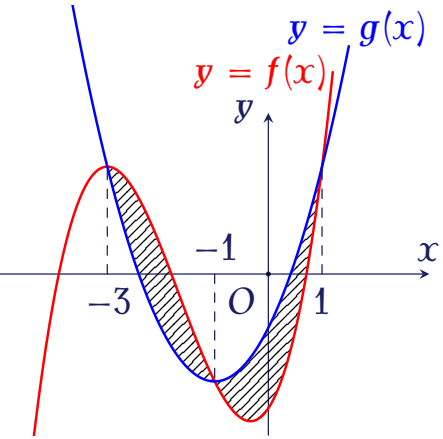
Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số $f(x)$ và $g(x)$ bằng
| $\dfrac{9}{2}$ | |
| $\dfrac{18}{5}$ | |
| $4$ | |
| $5$ |
Cho hàm số $y=f(x)$ liên tục trên $\mathbb{R}$. Gọi $S$ là diện tích hình phẳng giới hạn bởi đồ thị hàm số $y=f(x)$, trục hoành, đường thẳng $x=-1$, $x=5$ (như hình vẽ).
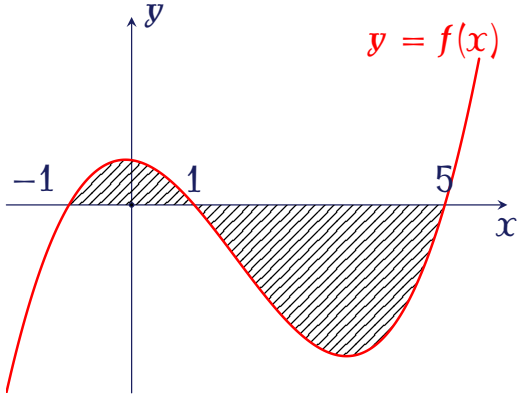
Mệnh đề nào sau đây đúng?
| $S=\displaystyle\displaystyle\int\limits_{-1}^{1}f(x)\mathrm{\,d}x+\displaystyle\int\limits_{1}^{5}f(x)\mathrm{\,d}x$ | |
| $S=-\displaystyle\displaystyle\int\limits_{-1}^{1}f(x)\mathrm{\,d}x-\displaystyle\int\limits_{1}^{5}f(x)\mathrm{\,d}x$ | |
| $S=\displaystyle\displaystyle\int\limits_{-1}^{1}f(x)\mathrm{\,d}x-\displaystyle\int\limits_{1}^{5}f(x)\mathrm{\,d}x$ | |
| $S=-\displaystyle\displaystyle\int\limits_{-1}^{1}f(x)\mathrm{\,d}x+\displaystyle\int\limits_{1}^{5}f(x)\mathrm{\,d}x$ |
Diện tích $S$ của phần hình phẳng được gạch chéo trong hình bên bằng
| $S=\displaystyle\displaystyle\int\limits_0^3\left|\dfrac{1}{2}{x^2}+\left(x^2-7x+12\right)\right|\mathrm{d}x$ | |
| $S=\displaystyle\displaystyle\int\limits_0^2\dfrac{1}{2}{x^2}\rm{d}x-\displaystyle\displaystyle\int\limits_2^3\left(x^2-7x+12\right)\mathrm{d}x$ | |
| $S=\displaystyle\displaystyle\int\limits_0^2\dfrac{1}{2}{x^2}\mathrm{d}x+\displaystyle\displaystyle\int\limits_2^3\left(x^2-7x+12\right)\mathrm{d}x$ | |
| $S=\displaystyle\displaystyle\int\limits_0^3\left|\dfrac{1}{2}{x^2}-\left(x^2-7x+12\right)\right|\mathrm{d}x$ |
Tính diện tích phần hình phẳng gạch chéo trong hình vẽ bên dưới.
| $1$ | |
| $\dfrac{7}{6}$ | |
| $\dfrac{5}{3}$ | |
| $\dfrac{7}{5}$ |
Gọi $S$ là diện tích hình phẳng giới hạn bởi đồ thị hàm số $y=f(x)$ và trục hoành (phần gạch sọc như hình vẽ).
Mệnh đề nào sau đây là đúng?
| $S=\displaystyle\displaystyle\int\limits_{a}^{c}f(x)\mathrm{d}x$ | |
| $S=\left|\displaystyle\displaystyle\int\limits_{a}^{b}f(x)\mathrm{d}x+\displaystyle\displaystyle\int\limits_{b}^{c}f(x)\mathrm{d}x\right|$ | |
| $S=\displaystyle\displaystyle\int\limits_{a}^{b}f(x)\mathrm{d}x-\displaystyle\displaystyle\int\limits_{b}^{c}f(x)\mathrm{d}x$ | |
| $S=\displaystyle\displaystyle\int\limits_{a}^{c}f(x)\mathrm{d}x-\displaystyle\displaystyle\int\limits_{a}^{b}f(x)\mathrm{d}x$ |
Cho hàm số $y=f(x)$ có đồ thị như hình vẽ bên dưới.

Diện tích $S$ của miền được tô đậm như hình vẽ được tính theo công thức nào sau đây?
| $S=-\displaystyle\displaystyle\int\limits_{0}^{3}f(x)\mathrm{\,d}x$ | |
| $S=\displaystyle\displaystyle\int\limits_{0}^{3}f(x)\mathrm{\,d}x$ | |
| $S=\displaystyle\displaystyle\int\limits_{0}^{4}f(x)\mathrm{\,d}x$ | |
| $S=-\displaystyle\displaystyle\int\limits_{0}^{4}f(x)\mathrm{\,d}x$ |
Diện tích hình phẳng giới hạn bởi hai parabol $y=x^2+3x-1$ và $y=-x^2+x+3$ được tô đậm trong hình bên có giá trị bằng
| $\displaystyle\displaystyle\int\limits_{-2}^{1}\left(4x+2\right)\mathrm{\,d}x$ | |
| $\displaystyle\displaystyle\int\limits_{-2}^{1}\left(2x^2+2x-4\right)\mathrm{\,d}x$ | |
| $\displaystyle\displaystyle\int\limits_{-2}^{1}\left(4-2x-2x^2\right)\mathrm{\,d}x$ | |
| $\displaystyle\displaystyle\int\limits_{-2}^{1}\left(-4x-2\right)\mathrm{\,d}x$ |
Cho hàm số $y=2^x$ có đồ thị là đường cong trong hình bên.
Diện tích $S$ của hình phẳng được tô đậm trong hình bằng
| $S=\displaystyle\displaystyle\int\limits_{1}^{2}2^x\mathrm{\,d}x$ | |
| $S=\displaystyle\displaystyle\int\limits_{0}^{2}2^{2x}\mathrm{\,d}x$ | |
| $S=\pi\displaystyle\displaystyle\int\limits_{0}^{2}2^x\mathrm{\,d}x$ | |
| $S=\displaystyle\displaystyle\int\limits_{0}^{2}2^x\mathrm{\,d}x$ |
Cho hình phẳng $D$ giới hạn bởi đồ thị của hai hàm số $y=f(x), y=g(x)$ (phần tô đậm trong hình vẽ).
Gọi $S$ là diện tích của hình phẳng $D$. Mệnh đề nào dưới đây đúng?
| $S=\displaystyle\displaystyle\int\limits_{-3}^0\left[f(x)-g(x)\right]\mathrm{\,d}x$ | |
| $S=\displaystyle\displaystyle\int\limits_{-3}^0\left[g(x)-f(x)\right]\mathrm{\,d}x$ | |
| $S=\displaystyle\displaystyle\int\limits_{-3}^0\left[f(x)+g(x)\right]\mathrm{\,d}x$ | |
| $S=\displaystyle\displaystyle\int\limits_{-3}^1\left[f(x)-g(x)\right]^2\mathrm{\,d}x$ |
Cho hàm số $y=f(x)$ có đồ thị như hình vẽ.
Diện tích phần tô đậm bằng
| $\displaystyle\displaystyle\int\limits_{-2}^{1}\left|f(x)\right|\mathrm{\,d}x$ | |
| $\displaystyle\displaystyle\int\limits_{0}^{1}\left|f(x)\right|\mathrm{\,d}x$ | |
| $\displaystyle\displaystyle\int\limits_{0}^{2}\left|f(x)\right|\mathrm{\,d}x$ | |
| $\displaystyle\displaystyle\int\limits_{-2}^{0}\left|f(x)\right|\mathrm{\,d}x$ |
Cho hàm số bậc ba $y=f(x)$ có đồ thị là đường cong trong hình bên.
Biết hàm số $f(x)$ đạt cực trị tại hai điểm $x_1$, $x_2$ thỏa mãn $x_2=x_1+2$ và $f\left(x_1\right)+f\left(x_2\right)=0$. Gọi $S_1$ và $S_2$ là diện tích của hai hình phẳng được gạch trong hình bên. Tỉ số $\dfrac{S_1}{S_2}$ bằng
| $\dfrac{3}{4}$ | |
| $\dfrac{5}{8}$ | |
| $\dfrac{3}{8}$ | |
| $\dfrac{3}{5}$ |
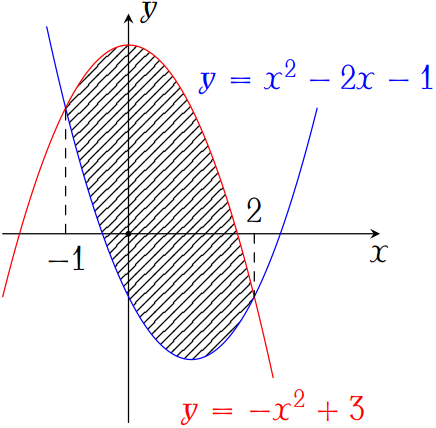
Diện tích phần hình phẳng gạch chéo trong hình vẽ trên được tính theo công thức nào dưới đây?
| \(\displaystyle\int\limits_{-1}^{2}(-2x+2)\mathrm{\,d}x\) | |
| \(\displaystyle\int\limits_{-1}^{2}(2x-2)\mathrm{\,d}x\) | |
| \(\displaystyle\int\limits_{-1}^{2}\left(-2x^2+2x+4\right)\mathrm{\,d}x\) | |
| \(\displaystyle\int\limits_{-1}^{2}\left(2x^2-2x-4\right)\mathrm{\,d}x\) |
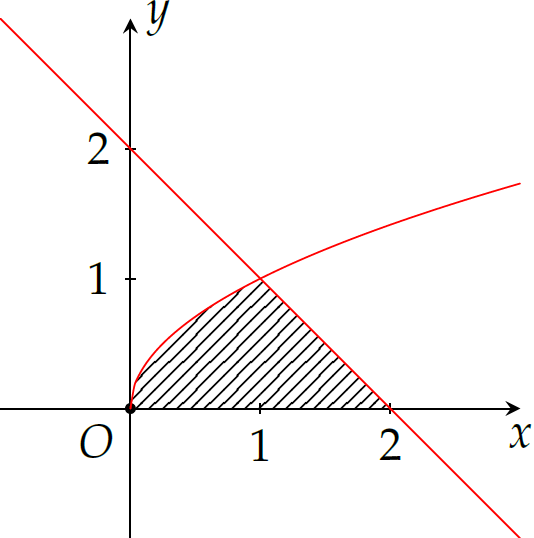
Cho \((H)\) là hình phẳng giới hạn bởi đồ thị của các hàm số \(y=\sqrt{x}\), \(y=0\), \(y=2-x\). Diện tích của \((H)\) là
| \(\dfrac{4\sqrt{2}-1}{3}\) | |
| \(\dfrac{8\sqrt{2}+3}{6}\) | |
| \(\dfrac{7}{6}\) | |
| \(\dfrac{5}{6}\) |
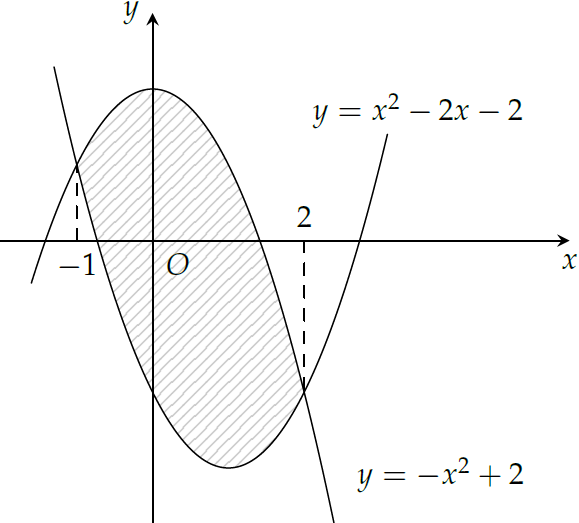
Diện tích phần hình phẳng được gạch chéo trong hình bên bằng
| \(\displaystyle\int\limits_{-1}^{2}{\left(-2x^2+2x+4\right)\mathrm{\,d}x}\) | |
| \(\displaystyle\int\limits_{-1}^{2}{\left(2x^2-2x-4\right)\mathrm{\,d}x}\) | |
| \(\displaystyle\int\limits_{-1}^{2}{\left(-2x^2-2x+4\right)\mathrm{\,d}x}\) | |
| \(\displaystyle\int\limits_{-1}^{2}{\left(2x^2+2x-4\right)\mathrm{\,d}x}\) |
Gọi tam giác cong \(OAB\) là hình phẳng giới hạn bởi đồ thị các hàm số \(y=2x^2\), \(y=3-x\), \(y=0\) (như hình vẽ).
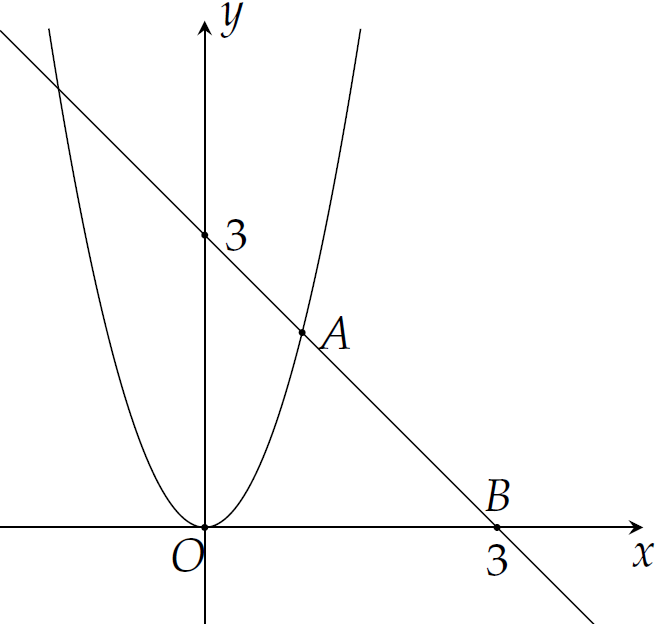
Tính diện tích \(S\) của tam giác cong \(OAB\).
| \(S=\dfrac{8}{3}\) | |
| \(S=\dfrac{4}{3}\) | |
| \(S=\dfrac{5}{3}\) | |
| \(S=\dfrac{10}{3}\) |
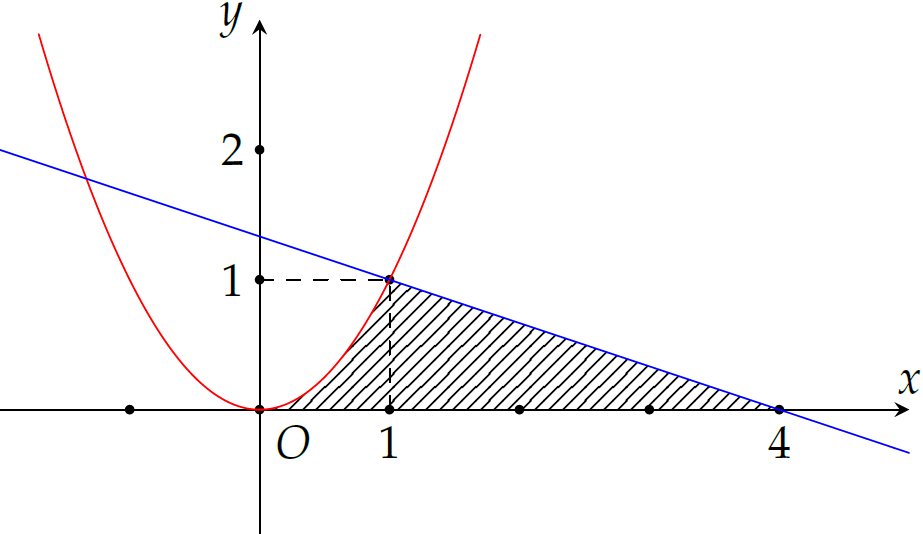
Tính diện tích hình phẳng giới hạn bởi các đường \(y=x^2\), \(y=-\dfrac{1}{3}x+\dfrac{4}{3}\) và trục hoành như hình vẽ.
| \(\dfrac{7}{3}\) | |
| \(\dfrac{56}{3}\) | |
| \(\dfrac{39}{2}\) | |
| \(\dfrac{11}{6}\) |
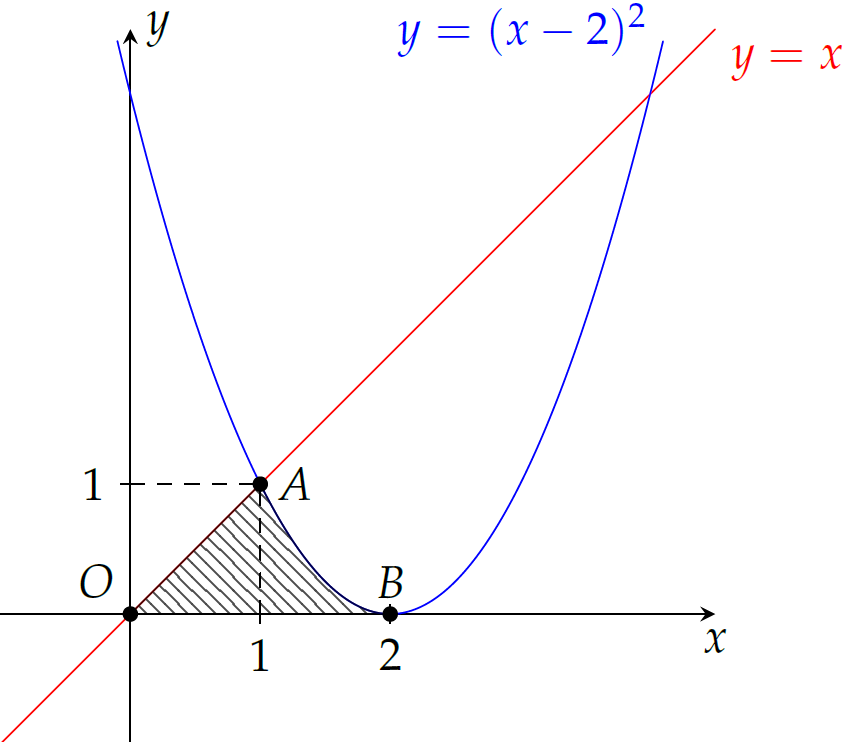
Tính diện tích phần hình phẳng gạch chéo (tam giác cong \(OAB\)) trong hình vẽ.
| \(\dfrac{5}{6}\) | |
| \(\dfrac{5\pi}{6}\) | |
| \(\dfrac{8}{15}\) | |
| \(\dfrac{8\pi}{15}\) |
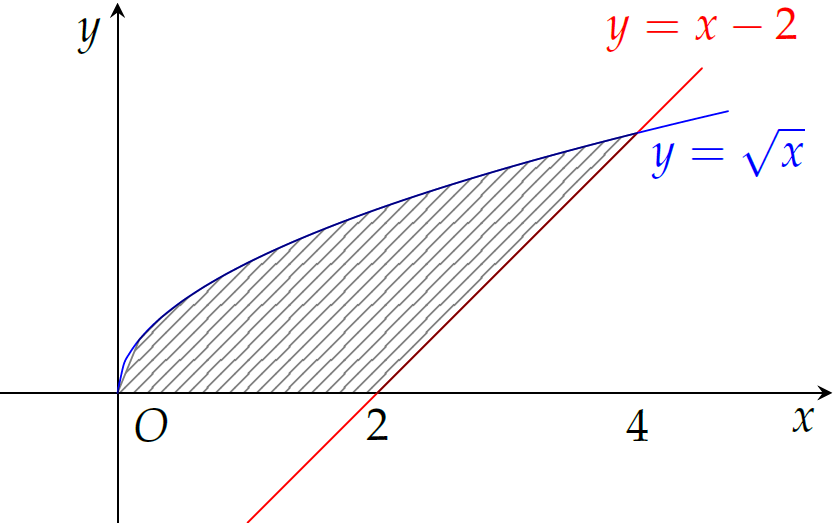
Tính diện tích \(S\) của hình phẳng (phần gạch sọc) trong hình.
| \(S=\dfrac{8}{3}\) | |
| \(S=\dfrac{10}{3}\) | |
| \(S=\dfrac{11}{3}\) | |
| \(S=\dfrac{7}{3}\) |
