Đồ thị hàm số $y=x^3-3x^2-9x+1$ có hai điểm cực trị là $A$ và $B$. Điểm nào sau đây thuộc đường thẳng $AB$?
| $M(0;-1)$ | |
| $Q(-1;10)$ | |
| $P(1;0)$ | |
| $N(1;-10)$ |
Viết phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số $y=-2x^3+3x^2+1$.
| $y=x+1$ | |
| $y=-x+1$ | |
| $y=x-1$ | |
| $y=-x-1$ |
Biết đồ thị hàm số $y=x^3-3x+1$ có hai điểm cực trị $A,\,B$. Khi đó đường thẳng $AB$ có phương trình
| $y=2x-1$ | |
| $y=x-2$ | |
| $y=-x+2$ | |
| $y=-2x+1$ |
Biết rằng đồ thị hàm số \(y=x^3-3x+1\) có hai điểm cực trị \(A,\,B\). Khi đó đường thẳng \(AB\) có phương trình là
| \(y=2x-1\) | |
| \(y=x-2\) | |
| \(y=-x+2\) | |
| \(y=1-2x\) |
Trong không gian $Oxyz$, cho hai điểm $M(-2;-2;1)$, $A(1;2;-3)$ và đường thẳng $d\colon\dfrac{x+1}{2}=\dfrac{y-5}{2}=\dfrac{z}{-1}$. Gọi $\overrightarrow{u}=(1;a;b)$ là một vectơ chỉ phương của đường thẳng $\Delta$ đi qua $M$, $\Delta$ vuông góc với đường thẳng $d$ đồng thời cách điểm $A$ một khoảng nhỏ nhất. Giá trị của $a+2b$ là
| $1$ | |
| $2$ | |
| $3$ | |
| $4$ |
Trong không gian $Oxyz$ cho hai điểm $A(1;2;-3)$, $M(-2;-2;1)$ và đường thẳng $d$ có phương trình $\dfrac{x+1}{2}=\dfrac{y-5}{2}=\dfrac{z}{-1}$. Phương trình đường thẳng $d'$ đi qua $M$ và vuông góc với $d$ sao cho khoảng cách từ điểm $A$ đến $d'$ nhỏ nhất là
| $\begin{cases}x=-2+t\\ y=-2\\ z=1+t\end{cases}$ | |
| $\begin{cases}x=-2\\ y=-2+t\\ z=1+2t\end{cases}$ | |
| $\begin{cases}x=-2+t\\ y=-2-t\\ z=1\end{cases}$ | |
| $\begin{cases}x=-2+t\\ y=-2\\ z=1+2t\end{cases}$ |
Trong không gian \(Oxyz\) cho mặt cầu \(\left(S\right)\colon x^2+y^2+z^2-6x+4y-2z+5=0\) và mặt phẳng \(\left(P\right)\colon x+2y+2z+11=0\). Tìm điểm \(M\) trên mặt cầu \(\left(S\right)\) sao cho khoảng cách từ \(M\) đến \(\left(P\right)\) là ngắn nhất.
| \(M\left(0;0;1\right)\) | |
| \(M\left(2;-4;-1\right)\) | |
| \(M\left(4;0;3\right)\) | |
| \(M\left(0;-1;0\right)\) |
Trong không gian \(Oxyz\), cho mặt cầu \(\left(S\right)\colon\left(x-2\right)^2+\left(y-1\right)^2+\left(z-1\right)^2=9\) và \(M\left(x_0;y_0;z_0\right)\in\left(S\right)\) sao cho \(A=x_0+2y_0+2z_0\) đạt giá trị nhỏ nhất. Khi đó \(x_0+y_0+z_0\) bằng
| \(2\) | |
| \(-1\) | |
| \(-2\) | |
| \(1\) |
Cho hàm số $y=f(x)$ có đạo hàm trên $\mathbb{R}$ và có bảng xét dấu $f'(x)$ như sau:

Hỏi hàm số $y=f\big(x^2-2x\big)$ có bao nhiêu điểm cực tiểu?
| $1$ | |
| $3$ | |
| $2$ | |
| $4$ |
Cho hàm số $f(x)$ liên tục trên $\mathbb{R}$ và có bảng xét dấu của đạo hàm như sau:

Số điểm cực đại của hàm số đã cho là
| $3$ | |
| $1$ | |
| $2$ | |
| $0$ |
Cho hàm số $y=f(x)$ có bảng xét dấu đạo hàm như sau:

Số điểm cực trị của hàm số đã cho bằng
| $3$ | |
| $0$ | |
| $1$ | |
| $2$ |
Cho hàm số $y=f(x)$ có đạo hàm $f'(x)=(x+2)^2(x-1)^5\big(x^2-2(m-6)x+m\big)$ với mọi $x\in\mathbb{R}$. Số giá trị nguyên dương của tham số $m$ để hàm số đã cho có đúng một điểm cực trị là
| $7$ | |
| $5$ | |
| $6$ | |
| $4$ |
Có bao nhiêu giá trị nguyên của tham số $a\in(-10;+\infty)$ để hàm số $y=\big|x^3+(a+2)x+9-a^2\big|$ đồng biến trên khoảng $(0;1)$?
| $12$ | |
| $11$ | |
| $6$ | |
| $5$ |
Có bao nhiêu giá trị nguyên của tham số $m$ để hàm số $y=-x^4+6x^2+mx$ có ba điểm cực trị?
| $17$ | |
| $15$ | |
| $3$ | |
| $7$ |
Cho hàm số $f(x)$, trong đó $f(x)$ là một đa giác. Hàm số $f'(x)$ có đồ thị như hình vẽ bên.
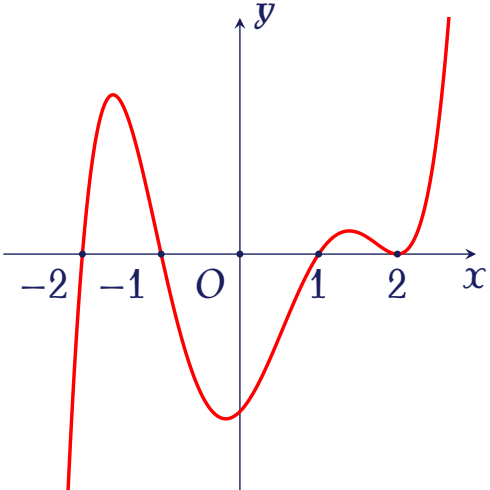
Hỏi có bao nhiêu giá trị nguyên $m$ thuộc $(-5;5)$ để hàm số $y=g(x)=f\big(x^2-2|x|+m\big)$ có $9$ điểm cực trị?
| $3$ | |
| $4$ | |
| $1$ | |
| $2$ |
Cho hàm số $y=f(x)$ có đạo hàm là $f'(x)=(x-1)^2(3-x)\big(x^2-x-1\big)$. Hỏi hàm số $f(x)$ có bao nhiêu điểm cực tiểu?
| $3$ | |
| $2$ | |
| $1$ | |
| $0$ |
Phát biểu nào sau đây đúng?
| Hàm số $y=f(x)$ đạt cực trị tại $x_0$ khi và chỉ khi $x_0$ là nghiệm của đạo hàm | |
| Nếu $f'\big(x_0\big)=0$ và $f''\big(x_0\big)>0$ thì hàm số đạt cực đại tại $x_0$ | |
| Nếu $f'\big(x_0\big)=0$ và $f''\big(x_0\big)=0$ thì $x_0$ không phải là cực trị của hàm số $y=f(x)$ đã cho | |
| Nếu $f'(x)$ đổi dấu khi $x$ qua điểm $x_0$ và $y=f(x)$ liên tục tại $x_0$ thì hàm số $y=f(x)$ đạt cực trị tại điểm $x_0$ |
Cho hàm số $f(x)$ liên tục trên $\mathbb{R}$ và có bảng xét dấu của đạo hàm như sau:

Số điểm cực đại của hàm số đã cho là
| $3$ | |
| $1$ | |
| $2$ | |
| $0$ |
Tìm giá trị nhỏ nhất của tham số $m$ để bất phương trình $$\dfrac{x^3+\sqrt{3x^2+1}+1}{\sqrt{x}-\sqrt{x-1}}\leq\dfrac{m}{\left(\sqrt{x}+\sqrt{x-1}\right)^2}$$có nghiệm.
| $m=1$ | |
| $m=4$ | |
| $m=13$ | |
| $m=8$ |
Tìm $m$ sao cho bất phương trình $\dfrac{x^2-2x+2}{x-1}\leq m$ có đúng một nghiệm trên khoảng $(1;+\infty)$.
| $m\geq2$ | |
| $m\leq2$ | |
| $m=2$ | |
| $m>2$ |
