Giá trị nhỏ nhất của hàm số $y=x^3+3x^2-1$ trên đoạn $[-1;1]$ bằng
| $3$ | |
| $-1$ | |
| $1$ | |
| $2$ |
Cho hàm số $f(x)=\dfrac{x+m}{x+1}$ với $m$ là tham số thực. Tìm giá trị của $m$ thỏa mãn $\min\limits_{[1;2]}f(x)+\min\limits_{[1;2]}f(x)=\dfrac{16}{3}$.
| $m=5$ | |
| $m=\dfrac{5}{6}$ | |
| $m=-5$ | |
| $m=\dfrac{5}{3}$ |
Cho hàm số $f(x)=\dfrac{x+m}{x-1}$ với $m$ là tham số thực. Gọi $m$ là giá trị thỏa mãn $\min\limits_{[2;4]}=3$, mệnh đề nào sau đây là đúng?
| $3< m\leq4$ | |
| $1\leq m<3$ | |
| $m>4$ | |
| $m<-1$ |
Cho hàm số $f(x)=\dfrac{x-m^2}{x+8}$ với $m$ là tham số thực. Tìm giá trị lớn nhất của $m$ để hàm số có giá trị nhỏ nhất trên đoạn $[0;3]$ bằng $-2$.
| $m=-4$ | |
| $m=5$ | |
| $m=1$ | |
| $m=4$ |
Giá trị nhỏ nhất của hàm số \(f\left(x\right)=x^3-24x\) trên đoạn \(\left[2;19\right]\) bằng
| \(32\sqrt{2}\) | |
| \(-40\) | |
| \(-32\sqrt{2}\) | |
| \(-45\) |
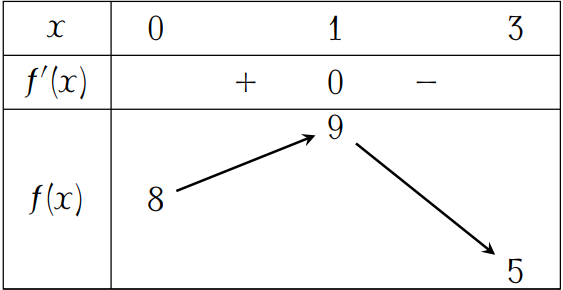
Cho hàm số \(y=f(x)\) có bảng biến thiên như hình. Gọi \(S\) là tập hợp các số nguyên dương \(m\) để bất phương trình $$f(x)\geq mx^2\left(x^2-2\right)+2m$$có nghiệm thuộc đoạn \([0;3]\). Số phần tử của tập \(S\) là
| \(9\) | |
| \(10\) | |
| Vô số | |
| \(0\) |
Một chất điểm chuyển động theo phương trình \(S=-2t^3+18t^2+1\), trong đó \(t\) tính bằng giây và \(S\) tính bằng mét. Mất bao lâu kể từ lúc xuất phát để chất điểm đạt vận tốc lớn nhất?
| \(5\) giây | |
| \(6\) giây | |
| \(3\) giây | |
| \(1\) giây |
Gọi \(M,\,N\) lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(y=x^3-3x^2+1\) trên đoạn \([1;2]\). Khi đó tổng \(M+N\) bằng
| \(2\) | |
| \(-2\) | |
| \(0\) | |
| \(-4\) |
Giá trị nhỏ nhất \(m\) của hàm số \(y=x^3-3x+5\) trên đoạn \([2;4]\) là
| \(0\) | |
| \(5\) | |
| \(7\) | |
| \(3\) |
Giá trị lớn nhất của hàm số \(y=x(5-2x)^2\) trên đoạn \([0;3]\) là
| \(\dfrac{250}{3}\) | |
| \(0\) | |
| \(\dfrac{250}{27}\) | |
| \(\dfrac{125}{27}\) |
Tìm giá trị lớn nhất của hàm số \(f(x)=x^3-5x^2+3x-1\) trên đoạn \([2;4]\).
| \(\max\limits_{[2;4]}f(x)=-5\) | |
| \(\max\limits_{[2;4]}f(x)=-10\) | |
| \(\max\limits_{[2;4]}f(x)=-7\) | |
| \(\max\limits_{[2;4]}f(x)=1\) |
Tìm giá trị lớn nhất của hàm số \(f(x)=2x^3+3x^2-12x+2\) trên đoạn \([-1;2]\).
| \(\max\limits_{[-1;2]}f(x)=10\) | |
| \(\max\limits_{[-1;2]}f(x)=6\) | |
| \(\max\limits_{[-1;2]}f(x)=11\) | |
| \(\max\limits_{[-1;2]}f(x)=15\) |
Tìm giá trị lớn nhất của hàm số \(f(x)=x^3-8x^2+16x-9\) trên đoạn \([1;3]\).
| \(\max\limits_{[1;3]}f(x)=5\) | |
| \(\max\limits_{[1;3]}f(x)=\dfrac{13}{27}\) | |
| \(\max\limits_{[1;3]}f(x)=-6\) | |
| \(\max\limits_{[1;3]}f(x)=0\) |
Giá trị lớn nhất của hàm số \(y=x^3-3x+4\) trên đoạn \([-2;2]\) là
| \(10\) | |
| \(6\) | |
| \(24\) | |
| \(4\) |
Giá trị nhỏ nhất của hàm số \(y=x^3-3x+5\) trên đoạn \([2;4]\) là
| \(3\) | |
| \(7\) | |
| \(5\) | |
| \(0\) |
Cho hàm số \(y=x^4+8x^2+m\) có giá trị nhỏ nhất trên \([1;3]\) bằng \(6\). Tham số thực \(m\) bằng
| \(-42\) | |
| \(6\) | |
| \(15\) | |
| \(-3\) |
Gọi \(S\) là tập hợp tất cả các giá trị thực của tham số \(m\) sao cho giá trị lớn nhất của hàm số \(f(x)=\left|x^3-3x+m\right|\) trên đoạn \(\left[0;3\right]\) bằng \(16\). Tổng tất cả các phần tử của \(S\) bằng
| \(-16\) | |
| \(16\) | |
| \(-12\) | |
| \(-2\) |
Cho hàm số $f(x)=ax^3+cx+d$ ($a\neq0$) có $\min\limits_{x\in(0;+\infty)}f(x)=f(2)$. Tìm giá trị lớn nhất của hàm số trên đoạn $[-3;1]$.
| $24a+d$ | |
| $d-16a$ | |
| $8a-d$ | |
| $d+16a$ |
Giá trị nhỏ nhất của hàm số $y=x^3-3x^2$ trên đoạn $[1;5]$ bằng
| $50$ | |
| $-4$ | |
| $-45$ | |
| $-2$ |
Có bao nhiêu giá trị nguyên của tham số $a\in(-10;+\infty)$ để hàm số $y=\big|x^3+(a+2)x+9-a^2\big|$ đồng biến trên khoảng $(0;1)$?
| $12$ | |
| $11$ | |
| $6$ | |
| $5$ |
