Tính diện tích hình phẳng giới hạn bởi hai đường cong \(y=x^3-x\) và \(y=x-x^2\).
| \(\dfrac{5}{12}\) | |
| \(\dfrac{37}{12}\) | |
| \(\dfrac{8}{3}\) | |
| \(\dfrac{9}{4}\) |
Cho hai hàm số $f(x)=mx^3+nx^2+px-\dfrac{5}{2}$ $(m,\,n,\,p\in\mathbb{R})$ và $g(x)=x^2+2x-1$ có đồ thị cắt nhau tại ba điểm có hoành độ lần lượt là $-3$, $-1$, $1$ (tham khảo hình vẽ bên).
Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số $f(x)$ và $g(x)$ bằng
| $\dfrac{9}{2}$ | |
| $\dfrac{18}{5}$ | |
| $4$ | |
| $5$ |
Diện tích $S$ của hình phẳng giới hạn bởi đồ thị của hai hàm số $y=-2x^3+x^2+x+5$ và $y=x^2-x+5$ bằng
| $S=\pi$ | |
| $S=\dfrac{1}{2}$ | |
| $S=0$ | |
| $S=1$ |
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y=x^3-x\) và đồ thị hàm số \(y=x-x^2\).
| \(\dfrac{37}{12}\) | |
| \(\dfrac{27}{4}\) | |
| \(13\) | |
| \(\dfrac{9}{4}\) |
Tính diện tích \(S\) của phần hình phẳng giới hạn bởi hai đồ thị hàm số \(y=x^3-3x^2\) và \(y=x^2+x-4\).
| \(S=\dfrac{253}{12}\) | |
| \(S=\dfrac{125}{12}\) | |
| \(S=\dfrac{16}{3}\) | |
| \(S=\dfrac{63}{4}\) |
Ba Tí muốn làm cửa sắt được thiết kế như hình.
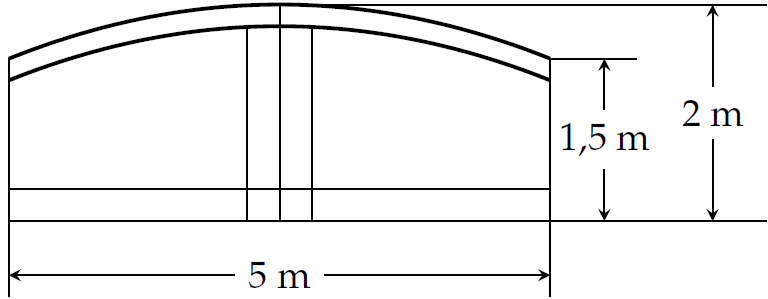
Vòm cổng có hình dạng một parabol. Giá \(1\)m\(^2\) cửa sắt là \(660000\) đồng. Cửa sắt có giá (nghìn đồng) là
| \(6500\) | |
| \(\dfrac{55}{6}\cdot10^3\) | |
| \(5600\) | |
| \(6050\) |
Trên bức tường cần trang trí một hình phẳng dạng parabol đỉnh \(S\) như hình vẽ, biết \(OS=AB=4\) cm, \(O\) là trung điểm \(AB\).
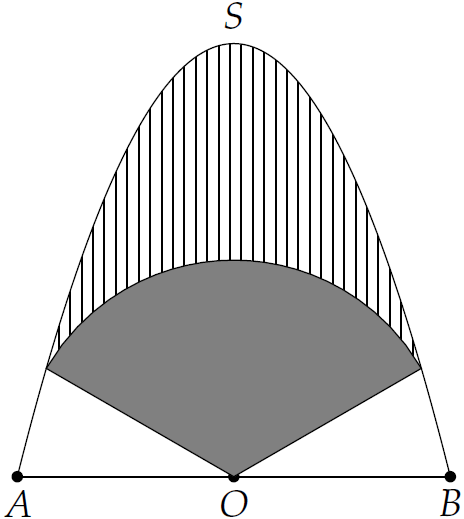
Parabol trên được chia thành ba phần để sơn ba màu khác nhau với mức chi phí: phần trên là phần kẻ sọc \(140000\) đồng/m\(^2\), phần giữa là hình quạt tâm \(O\), bán kính \(2\) m được tô đậm \(150000\) đồng/m\(^2\), phần còn lại \(160000\) đồng/m\(^2\). Tổng chi phí để sơn cả ba phần gần nhất với số nào sau đây?
| \(1.597.000\) đồng | |
| \(1.625.000\) đồng | |
| \(1.575.000\) đồng | |
| \(1.600.000\) đồng |
Một viên gạch hoa hình vuông cạnh \(40\) cm. Người ta đã dùng bốn đường parabol có chung đỉnh tại tâm của viên gạch để tạo ra bốn cánh hoa (phần tô đậm như hình vẽ).
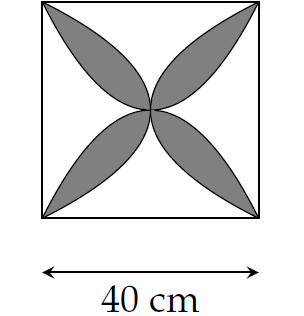
Diện tích của mỗi cánh hoa đó bằng
| \(200\) cm\(^2\) | |
| \(\dfrac{800}{3}\) cm\(^2\) | |
| \(\dfrac{400}{3}\) cm\(^2\) | |
| \(\dfrac{200}{3}\) cm\(^2\) |
Bạn An cần mua một chiếc gương có viền là đường parabol bậc hai (như hình vẽ).
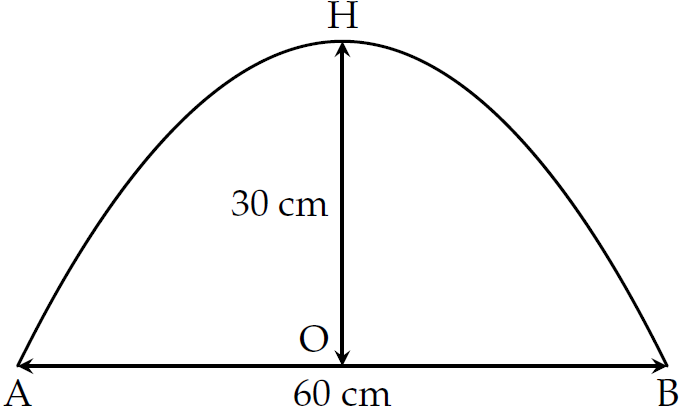
Biết rằng đoạn \(AB=60\) cm, \(OH=30\) cm. Diện tích của chiếc gương bạn An mua là
| \(1000\) cm\(^2\) | |
| \(1400\) cm\(^2\) | |
| \(1200\) cm\(^2\) | |
| \(900\) cm\(^2\) |
Gọi tam giác cong \(OAB\) là hình phẳng giới hạn bởi đồ thị các hàm số \(y=2x^2\), \(y=3-x\), \(y=0\) (như hình vẽ).
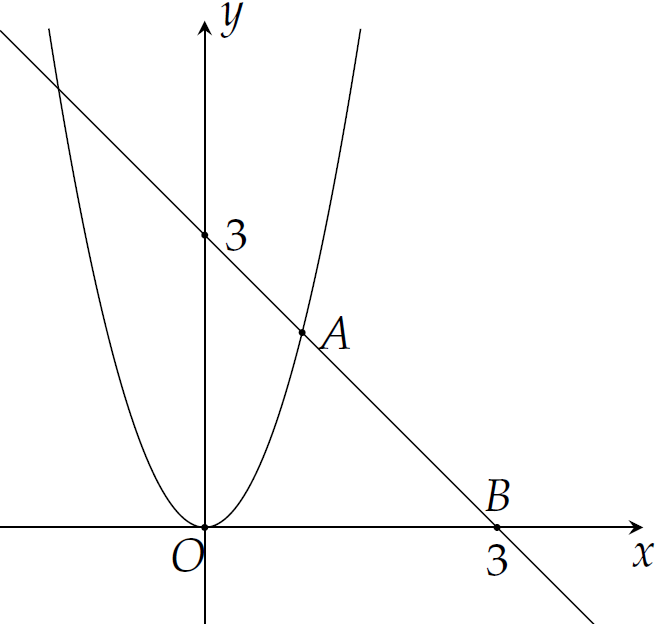
Tính diện tích \(S\) của tam giác cong \(OAB\).
| \(S=\dfrac{8}{3}\) | |
| \(S=\dfrac{4}{3}\) | |
| \(S=\dfrac{5}{3}\) | |
| \(S=\dfrac{10}{3}\) |
Tính diện tích hình phẳng giới hạn bởi các đường \(y=x^2\), \(y=\dfrac{x^2}{8}\), \(y=\dfrac{27}{x}\).
| \(\dfrac{63}{8}\) | |
| \(27\ln2-\dfrac{63}{8}\) | |
| \(27\ln2\) | |
| \(27\ln2-\dfrac{63}{4}\) |
Tính diện tích hình phẳng giới hạn bởi các đường \(y=x^2\), \(y=-\dfrac{1}{3}x+\dfrac{4}{3}\) và trục hoành như hình vẽ.
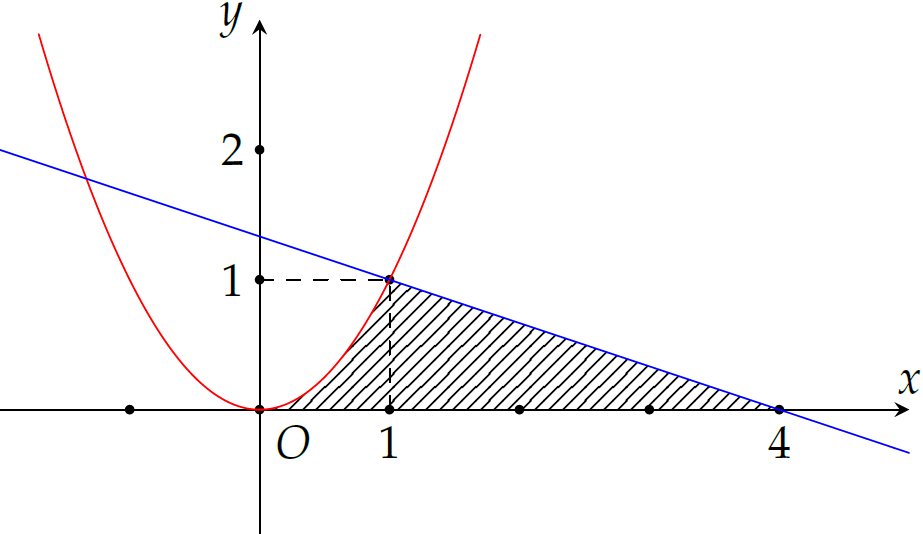
| \(\dfrac{7}{3}\) | |
| \(\dfrac{56}{3}\) | |
| \(\dfrac{39}{2}\) | |
| \(\dfrac{11}{6}\) |
Tính diện tích phần hình phẳng gạch chéo (tam giác cong \(OAB\)) trong hình vẽ.
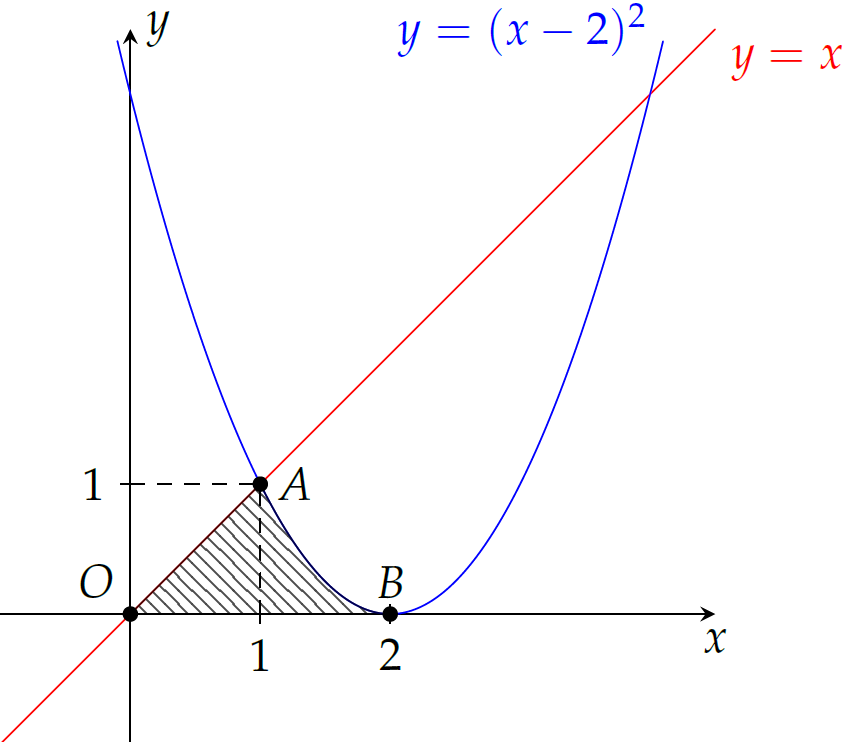
| \(\dfrac{5}{6}\) | |
| \(\dfrac{5\pi}{6}\) | |
| \(\dfrac{8}{15}\) | |
| \(\dfrac{8\pi}{15}\) |
Tính diện tích \(S\) của hình phẳng giới hạn bởi đồ thị hàm số \(y=-x^3+3x^2-4\) và trục hoành.
| \(S=\dfrac{27}{4}\) | |
| \(S=\dfrac{27\pi}{4}\) | |
| \(S=4\) | |
| \(S=1\) |
Tính diện tích miền phẳng giới hạn bởi các đường \(y=x^3+2x+1\), trục hoành, \(x=1\) và \(x=2\).
| \(\dfrac{31}{4}\) | |
| \(\dfrac{49}{4}\) | |
| \(\dfrac{21}{4}\) | |
| \(\dfrac{39}{4}\) |
Cho hàm số $y=f(x)$ có đạo hàm liên tục trên $\mathbb{R}$ và thỏa mãn $f(x)+x f'(x)=4x^3-6x^2$, $\forall x\in\mathbb{R}$. Diện tích hình phẳng giới hạn bởi các đường $y=f(x)$ và $y=f'(x)$ bằng
| $\dfrac{7}{12}$ | |
| $\dfrac{45}{4}$ | |
| $\dfrac{1}{2}$ | |
| $\dfrac{71}{6}$ |
Diện tích hình phẳng giới hạn bởi đồ thị của hàm số $y=x^5$, trục hoành và hai đường thẳng $x=-1$, $x=1$ bằng
| $\dfrac{3}{2}$ | |
| $\dfrac{1}{3}$ | |
| $7$ | |
| $5$ |
Cho hàm số $f(x)=x^3+ax^2+bx+c$ với $a,\,b,\,c$ là các số thực. Biết hàm số $g(x)=f(x)+f'(x)+f''(x)$ có hai giá trị cực trị là $-3$ và $6$. Diện tích hình phẳng giới hạn bởi các đường $y=\dfrac{f(x)}{g(x)+6}$ và $y=1$ bằng
| $2\ln3$ | |
| $\ln3$ | |
| $\ln18$ | |
| $2\ln2$ |
Tính diện tích $S$ của hình phẳng giới hạn bởi đồ thị hàm số $y=x^2-4x$, $Ox$ và $x=0,\,x=2$.
| $S=9$ | |
| $S=\dfrac{16}{3}$ | |
| $S=\dfrac{32}{3}$ | |
| $S=\dfrac{5}{3}$ |
Cho hàm số $f(x)=3x^4+ax^3+bx^2+cx+d$ $(a,\,b,\,c,\,d\in\mathbb{R})$ có ba điểm cực trị là $-2,\,-1$ và $1$. Gọi $y=g(x)$ là hàm số bậc hai có đồ thị đi qua ba điểm cực trị của đồ thị hàm số $y=f(x)$. Diện tích hình phẳng giới hạn bởi hai đường $y=f(x)$ và $y=g(x)$ bằng
| $\dfrac{500}{81}$ | |
| $\dfrac{36}{5}$ | |
| $\dfrac{2932}{405}$ | |
| $\dfrac{2948}{405}$ |
