Trong mặt phẳng $Oxy$, phép quay tâm $O$ góc quay $-90^\circ$ biến $M(-3;5)$ thành điểm có tọa độ

	$(-5;-3)$
	$(5;-3)$
	$(5;3)$
	$(-5;3)$

Trong mặt phẳng $Oxy$, cho điểm $A(1;0)$. Ảnh của $A$ qua phép quay tâm $O$ góc quay $90^\circ$ là

	$A’(0;-1)$
	$A’(-1;0)$
	$A’(0;1)$
	$A’(1;1)$

Trong mặt phẳng $Oxy$, cho đường tròn $(\mathscr{C})\colon x^2+y^2-4x-2y=0$. Phép quay tâm $I$ góc $\dfrac{\pi}{4}$ biến $(\mathscr{C})$ thành chính nó. Tìm tọa độ tâm quay $I$.

	$I(0;0)$
	$I(2;1)$
	$I(1;2)$
	$I(1;1)$

Trong mặt phẳng $Oxy$, cho đường thẳng $d\colon3x-2y-1=0$. Ảnh của $d$ qua phép quay tâm $O$ góc $180^\circ$ có phương trình

	$3x+2y+1=0$
	$-3x+2y-1=0$
	$3x+2y-1=0$
	$3x-2y-1=0$

Trong mặt phẳng $Oxy$, điểm $M'(3;-2)$ là ảnh của điểm nào sau đây qua phép quay $Q_{(O,180^\circ)}$?

	$M(3;2)$
	$M(2;3)$
	$M(-3;2)$
	$M(-2;-3)$

Trong mặt phẳng $Oxy$, cho các điểm $I(3;1)$ và $J(-1;-1)$. Tìm ảnh của $J$ qua phép quay $\mathrm{Q}_{(I,-90^\circ)}$.

	$J'(-3;3)$
	$J'(1;-5)$
	$J'(1;5)$
	$J'(5;-3)$

Trong mặt phẳng $Oxy$, ảnh của đường tròn $(\mathscr{C})\colon(x+2)^2+(y-3)^2=9$ qua phép quay $\mathrm{Q}_{(O,90^\circ)}$ là đường tròn có phương trình

	$(x+2)^2+(y+3)^2=9$
	$(x+3)^2+(y+2)^2=9$
	$(x-3)^2+(y+2)^2=9$
	$(x+2)^2+(y-3)^2=9$

Trong mặt phẳng $Oxy$, cho điểm $M(2;2)$. Trong bốn điểm sau, điểm nào là ảnh của $M$ qua phép quay tâm $O$ góc $-45^\circ$?

	$M'\left(2;-2\sqrt{2}\right)$
	$M'\left(2\sqrt{2};2\right)$
	$M'\left(0;2\sqrt{2}\right)$
	$M'\left(2\sqrt{2};0\right)$

Trong mặt phẳng $Oxy$, ảnh của điểm $M(3;4)$ qua phép quay $\mathrm{Q}_{(O,45^\circ)}$ là

	$M'\left(\dfrac{7\sqrt{2}}{2};\dfrac{7\sqrt{2}}{2}\right)$
	$M'\left(-\dfrac{\sqrt{2}}{2};\dfrac{7\sqrt{2}}{2}\right)$
	$M'\left(-\dfrac{\sqrt{2}}{2};-\dfrac{\sqrt{2}}{2}\right)$
	$M'\left(\dfrac{7\sqrt{2}}{2};-\dfrac{\sqrt{2}}{2}\right)$

Trong mặt phẳng $Oxy$, cho đường thẳng $d\colon y=x$. Tìm ảnh của $d$ qua phép quay tâm $O$ góc $90^\circ$.

	$d'\colon y=2x$
	$d'\colon y=-x$
	$d'\colon y=-2x$
	$d'\colon y=x$

Trong mặt phẳng $Oxy$, cho đường thẳng $d\colon3x-y+2=0$. Tìm phương trình đường thẳng $d'$ là ảnh của $d$ qua phép quay tâm $O$ góc $-90^\circ$.

	$d'\colon3x-y-6=0$
	$d'\colon x-3y-2=0$
	$d'\colon x+3y-2=0$
	$d'\colon x-3y+2=0$

Trong mặt phẳng $Oxy$, cho điểm $B(-3;6)$. Tìm tọa độ điểm $E$ sao cho $B$ là ảnh của điểm $E$ qua phép quay tâm $O$ góc $-90^\circ$.

	$E(6;3)$
	$E(-3;-6)$
	$E(-6;-3)$
	$E(3;6)$

Trong mặt phẳng $Oxy$, ảnh của điểm $M(-6;1)$ qua phép quay $\mathrm{Q}_{(O,-90^\circ)}$ là

	$M'(1;6)$
	$M'(-1;-6)$
	$M'(-6;-1)$
	$M'(6;1)$

Trong mặt phẳng $Oxy$, phép quay tâm $O$ góc quay $90^\circ$ biến điểm $M(-1;2)$ thành điểm $M'$ có tọa độ là

	$(2;1)$
	$(2;-1)$
	$(-2;-1)$
	$(-2;1)$

Trong mặt phẳng $Oxy$, cho vectơ $\overrightarrow{v}=(-3;1)$ và parabol $(\mathscr{P})\colon y=1-x^2$. Phép tịnh tiến $\mathrm{T}_{\overrightarrow{v}}$ biến $(\mathscr{P})$ thành parabol $(\mathscr{P}')\colon y=ax^2+bx+c$. Tính $M=b+c-a$.

	$M=-1$
	$M=2$
	$M=11$
	$M=-12$

Trong mặt phẳng \(Oxy\) cho đường tròn \((x-8)^2+(y-3)^2=7\). Ảnh của đường tròn qua phép quay tâm \(O\) góc \(90^\circ\) là

	\((x+3)^2+(y-8)^2=4\)
	\((x+8)^2+(y-3)^2=7\)
	\((x+8)^2+(y+3)^2=7\)
	\((x+3)^2+(y-8)^2=7\)

Trong mặt phẳng \(Oxy\), ảnh của điểm \(M\left(-6;1\right)\) qua phép quay \(\mathrm{Q}_{\left(O,90^\circ\right)}\) là

	\(M'\left(1;6\right)\)
	\(M'\left(-1;-6\right)\)
	\(M'\left(-6;-1\right)\)
	\(M'\left(6;1\right)\)

Trong mặt phẳng $Oxy$, cho đường tròn $\left(\mathscr{C}\right)\colon(x+3)^2+(y-1)^2=5$ và $\overrightarrow{v}=(2;1)$. Viết phương trình đường tròn $(\mathscr{C}’)$ là ảnh của $(\mathscr{C})$ qua phép tịnh tiến theo vectơ $\overrightarrow{v}$.

Cho hình vuông $ABCD$ tâm $O$ (như hình).

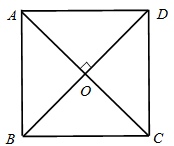
Xác định ảnh của tam giác $OBC$ qua phép quay tâm $O$ góc quay $\dfrac{\pi}{2}$?

	$\triangle OCB$
	$\triangle OAD$
	$\triangle OAB$
	$\triangle OCD$

Phép quay $\mathrm{Q}_{(O,\varphi)}$ biến đường tròn $(\mathscr{C})$ có bán kính $R$ thành đường tròn $(\mathscr{C}')$ có bán kính $R'$. Khẳng định nào sau đây đúng?

	$R'=3R$
	$R'=-3R$
	$R'=\dfrac{1}{3}R$
	$R'=R$