Cho phép quay $\mathrm{Q}_{(O,\varphi)}$ biến điểm $M$ thành $M'$. Khẳng định nào sau đây là khẳng định đúng?
| $\overrightarrow{OM}=\overrightarrow{OM'}$ và $\left(OM,OM'\right)=\varphi$ | |
| $OM=OM'$ và $\left(OM,OM'\right)=\varphi$ | |
| $\overrightarrow{OM}=\overrightarrow{OM'}$ và $\widehat{MOM'}=\varphi$ | |
| $OM=OM'$ và $\widehat{MOM'}=\varphi$ |
Trong mặt phẳng $Oxy$, biết rằng phép quay tâm $O$ góc $\alpha$ là phép đồng nhất, tìm số đo của $\alpha$.
| $\alpha=k\pi\,(k\in\mathbb{Z})$ | |
| $\alpha=k2\pi\,(k\in\mathbb{Z})$ | |
| $\alpha=0$ | |
| $\alpha=\dfrac{\pi}{2}$ |
Trong mặt phẳng $Oxy$, biểu thức tọa độ của phép quay $\mathrm{Q}_{\left(O,-\tfrac{\pi}{2}\right)}$ là
| $\begin{cases}x'=y\\ y'=x\end{cases}$ | |
| $\begin{cases}x'=-y\\ y'=-x\end{cases}$ | |
| $\begin{cases}x'=-y\\ y'=x\end{cases}$ | |
| $\begin{cases}x'=y\\ y'=-x\end{cases}$ |
Trong mặt phẳng $Oxy$, biểu thức tọa độ của phép quay $\mathrm{Q}_{\left(O,\tfrac{\pi}{2}\right)}$ là
| $\begin{cases}x'=y\\ y'=-x\end{cases}$ | |
| $\begin{cases}x'=-y\\ y'=-x\end{cases}$ | |
| $\begin{cases}x'=-y\\ y'=x\end{cases}$ | |
| $\begin{cases}x'=y\\ y'=x\end{cases}$ |
Trong mặt phẳng $Oxy$, biểu thức tọa độ của phép quay $\mathrm{Q}_{\left(O,\pi\right)}$ là
| $\begin{cases}x'=-x\\ y'=-y\end{cases}$ | |
| $\begin{cases}x'=-x\\ y'=y\end{cases}$ | |
| $\begin{cases}x'=x\\ y'=-y\end{cases}$ | |
| $\begin{cases}x'=x\\ y'=y\end{cases}$ |
Trong mặt phẳng $Oxy$, cho điểm $I(a;b)$. Biểu thức tọa độ của phép quay $\mathrm{Q}_{\left(I,\varphi\right)}$ là
| $\begin{cases}x'=x\cos\varphi-y\sin\varphi\\ y'=x\sin\varphi+y\cos\varphi\end{cases}$ | |
| $\begin{cases}x'=(x-a)\cos\varphi-(y-b)\sin\varphi\\ y'=(x-a)\sin\varphi+(y-b)\cos\varphi\end{cases}$ | |
| $\begin{cases}x'=(x-a)\cos\varphi-(y-b)\sin\varphi-a\\ y'=(x-a)\sin\varphi+(y-b)\cos\varphi-b\end{cases}$ | |
| $\begin{cases}x'=(x-a)\cos\varphi-(y-b)\sin\varphi+a\\ y'=(x-a)\sin\varphi+(y-b)\cos\varphi+b\end{cases}$ |
Cho phép quay $\mathrm{Q}_{(O,\varphi)}$ biến điểm $A$ thành điểm $A'$ và biến điểm $M$ thành điểm $M'$. Mệnh đề nào sau đây là sai?
| $\overrightarrow{AM}=\overrightarrow{A'M'}$ | |
| $(OA,OA')=\widehat{(OM,OM')}=\varphi$ | |
| $\big(\overrightarrow{AM},\overrightarrow{AM'}\big)=\varphi$ với $0\leq\varphi\leq\pi$ | |
| $AM=A'M'$ |
Biểu thức tọa độ của phép quay \(\mathrm{Q}_{\left(O,-90^\circ\right)}\) là
| \(\begin{cases}x'=-y\\ y'=x\end{cases}\) | |
| \(\begin{cases}x'=x\\ y'=-y\end{cases}\) | |
| \(\begin{cases}x'=-x\\ y'=y\end{cases}\) | |
| \(\begin{cases}x'=y\\ y'=-x\end{cases}\) |
Cho tam giác đều \(ABC\). Hãy xác định góc quay \(\varphi\) của phép quay tâm \(A\) biến điểm \(B\) thành điểm \(C\).
| \(\varphi=30^\circ\) | |
| \(\varphi=90^\circ\) | |
| \(\varphi=-120^\circ\) | |
| \(\varphi=60^\circ\) hoặc \(\varphi=-60^\circ\) |
Cho hình vuông tâm \(O\). Với giá trị nào của \(\varphi\) thì phép quay \(\mathrm{Q}_{\left(O,\varphi\right)}\) biến hình vuông đã cho thành chính nó?
| \(\varphi=\dfrac{\pi}{6}\) | |
| \(\varphi=\dfrac{\pi}{4}\) | |
| \(\varphi=\dfrac{\pi}{3}\) | |
| \(\varphi=\dfrac{\pi}{2}\) |
Cho tam giác đều tâm \(O\). Với giá trị nào của \(\varphi\) thì phép quay \(\mathrm{Q}_{\left(O,\varphi\right)}\) biến tam giác đều đã cho thành chính nó?
| \(\varphi=\dfrac{\pi}{3}\) | |
| \(\varphi=\dfrac{2\pi}{3}\) | |
| \(\varphi=\dfrac{3\pi}{2}\) | |
| \(\varphi=\dfrac{\pi}{2}\) |
Trong các mệnh đề sau, mệnh đề nào sai?
| Phép quay biến đường thẳng thành đường thẳng song song hoặc trùng với nó | |
| Phép quay biến đoạn thẳng thành đoạn thẳng có độ dài bằng nó | |
| Phép quay biến đường tròn thành đường tron có bán kính bằng nó | |
| Phép quay là một phép dời hình |
Mệnh đề nào sau đây là sai?
| Phép quay bảo toàn khoảng cách giữa hai điểm bất kì | |
| Phép tịnh tiến biến một đường thẳng thành một đường thẳng song song với nó | |
| Phép tịnh tiến biến ba điểm thẳng hàng thành ba điểm thẳng hàng | |
| Phép quay biến một đường tròn thành một đườg tròn có cùng bán kính |
Cho hình vuông $ABCD$ tâm $O$ (như hình).
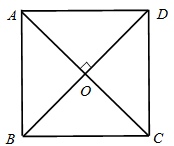
Xác định ảnh của tam giác $OBC$ qua phép quay tâm $O$ góc quay $\dfrac{\pi}{2}$?
| $\triangle OCB$ | |
| $\triangle OAD$ | |
| $\triangle OAB$ | |
| $\triangle OCD$ |
Trong mặt phẳng $Oxy$, phép quay tâm $O$ góc quay $-90^\circ$ biến $M(-3;5)$ thành điểm có tọa độ
| $(-5;-3)$ | |
| $(5;-3)$ | |
| $(5;3)$ | |
| $(-5;3)$ |
Phép quay $\mathrm{Q}_{(O,\varphi)}$ biến đường tròn $(\mathscr{C})$ có bán kính $R$ thành đường tròn $(\mathscr{C}')$ có bán kính $R'$. Khẳng định nào sau đây đúng?
| $R'=3R$ | |
| $R'=-3R$ | |
| $R'=\dfrac{1}{3}R$ | |
| $R'=R$ |
Trong mặt phẳng $Oxy$, cho điểm $A(1;0)$. Ảnh của $A$ qua phép quay tâm $O$ góc quay $90^\circ$ là
| $A’(0;-1)$ | |
| $A’(-1;0)$ | |
| $A’(0;1)$ | |
| $A’(1;1)$ |
Trong mặt phẳng $Oxy$, cho điểm $M'(x';y')$ là ảnh của điểm $M(x;y)$ qua phép tịnh tiến theo vectơ $\overrightarrow{v}=(a;b)$. Tìm mệnh đề đúng?
| $\begin{cases}x'=x+b\\ y'=y+a\end{cases}$ | |
| $\begin{cases}x'=a-x\\ y'=b-y\end{cases}$ | |
| $\begin{cases}x'=x+a\\ y'=y+b\end{cases}$ | |
| $\begin{cases}x'=x-a\\ y'=y-b\end{cases}$ |
Trong mặt phẳng $Oxy$, cho bốn điểm $A(-1;2)$, $B(3;-1)$, $A'(9;-4)$, $B'(5;-1)$. Phép quay tâm $I(a;b)$ biến điểm $A$ thành $A'$, điểm $B$ thành $B'$, khi đó giá trị $a+b$ bằng
| $5$ | |
| $4$ | |
| $3$ | |
| $2$ |
Trong mặt phẳng $Oxy$, cho đường tròn $(\mathscr{C})\colon x^2+y^2-4x-2y=0$. Phép quay tâm $I$ góc $\dfrac{\pi}{4}$ biến $(\mathscr{C})$ thành chính nó. Tìm tọa độ tâm quay $I$.
| $I(0;0)$ | |
| $I(2;1)$ | |
| $I(1;2)$ | |
| $I(1;1)$ |
