Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông tại $A$, $\widehat{ABC}=30^\circ$. Tam giác $SBC$ là tam giác đều cạnh $a$ và nằm trong mặt phẳng vuông góc với đáy. Thể tích khối chóp $S.ABC$ là
| $\dfrac{3a^3}{16}$ | |
| $\dfrac{a^3}{16}$ | |
| $\dfrac{a^3\sqrt{3}}{16}$ | |
| $\dfrac{3\sqrt{3}a^3}{16}$ |
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $a$, tam giác $SAB$ đều và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp $S.ABC$.
| $\dfrac{a^3\sqrt{3}}{18}$ | |
| $\dfrac{a^3\sqrt{3}}{12}$ | |
| $\dfrac{a^3}{8}$ | |
| $\dfrac{a^3}{6}$ |
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật và $AD=a$, $AB=2a$. Biết tam giác $SAB$ là tam giác đều và mặt phẳng $(SAB)$ vuông góc với mặt phẳng $(ABCD)$. Tính khoảng cách từ điểm $A$ đến mặt phẳng $(SBD)$.
| $\dfrac{a\sqrt{3}}{4}$ | |
| $\dfrac{a\sqrt{3}}{2}$ | |
| $a\sqrt{3}$ | |
| $\dfrac{a\sqrt{3}}{3}$ |
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $a$. Mặt bên $(SAB)$ là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng $(ABC)$. Tính theo $a$ thể tích $V$ của khối chóp $S.ABC$.
| $V=\dfrac{a^3}{24}$ | |
| $V=\dfrac{a^3}{4}$ | |
| $V=\dfrac{3a^3}{8}$ | |
| $V=\dfrac{a^3}{8}$ |
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật và $AD=a$, $AB=2a$. Biết tam giác $SAB$ là tam giác đều và mặt phẳng $(SAB)$ vuông góc với mặt phẳng $(ABCD)$. Tính khoảng cách từ điểm $A$ đến mặt phẳng $(SBD)$.
| $\dfrac{a\sqrt{3}}{4}$ | |
| $\dfrac{a\sqrt{3}}{2}$ | |
| $a\sqrt{3}$ | |
| $\dfrac{a\sqrt{3}}{3}$ |
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông tại $A$, $AB=a$, $AC=2a$, $SA$ vuông góc với mặt phẳng đáy và $SB$ tạo với mặt đáy một góc $60^\circ$. Gọi $M,\,N$ lần lượt là trung điểm của $SB$ và $BC$. Thể tích khối chóp $A.SCNM$ bằng
| $\dfrac{\sqrt{3}}{4}a^3$ | |
| $\dfrac{\sqrt{3}}{2}a^3$ | |
| $\dfrac{3\sqrt{3}}{4}a^3$ | |
| $\dfrac{3\sqrt{3}}{2}a^3$ |
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $a$. Hình chiếu vuông góc của $S$ trên đáy là điểm $H$ trên cạnh $AC$ sao cho $AH=\dfrac{2}{3}AC$; mặt phẳng $(SBC)$ tạo với đáy một góc $60^{\circ}$. Thể tích khối chóp $S.ABC$ là
| $\dfrac{a^3\sqrt{3}}{12}$ | |
| $\dfrac{a^3\sqrt{3}}{48}$ | |
| $\dfrac{a^3\sqrt{3}}{36}$ | |
| $\dfrac{a^3\sqrt{3}}{24}$ |
Cho khối chóp đều $S.ABCD$ có $AC=4a$, hai mặt phẳng $(SAB)$ và $(SCD)$ vuông góc với nhau. Thể tích của khối chóp đã cho bằng
| $\dfrac{16\sqrt{2}}{3}a^3$ | |
| $\dfrac{8\sqrt{2}}{3}a^3$ | |
| $16a^3$ | |
| $\dfrac{16}{3}a^3$ |
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $a$, cạnh bên $SA$ vuông góc với mặt phẳng đáy, góc giữa $SA$ và mặt phẳng $(SBC)$ bằng $45^\circ$ (tham khảo hình bên).
Thể tích của khối chóp $S.ABC$ bằng
| $\dfrac{a^3}{8}$ | |
| $\dfrac{3a^3}{8}$ | |
| $\dfrac{\sqrt{3}a^3}{12}$ | |
| $\dfrac{a^3}{4}$ |
Cho hình chóp \(S.ABC\) có đáy là tam giác đều cạnh \(a\), cạnh bên \(SA=2a\) và vuông góc với mặt đáy. Gọi \(M,\,N\) lần lượt là hình chiếu vuông góc của \(A\) trên các đường thẳng \(SB\), \(SC\).
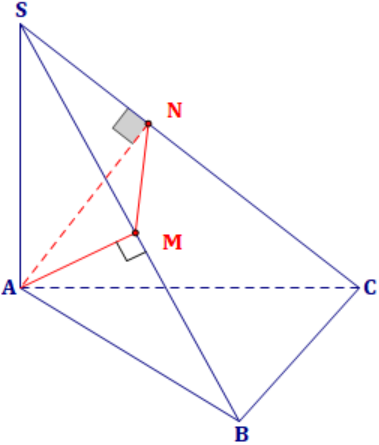
 Tính thể tích của khối chóp \(A.BCNM\).
Tính thể tích của khối chóp \(A.BCNM\).
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành và có thể tích bằng $1$. Trên cạnh $SC$ lấy điểm $E$ sao cho $SE=2EC$. Tính thể tích $V$ của khối tứ diện $SEBD$.
| $V=\dfrac{1}{12}$ | |
| $V=\dfrac{1}{3}$ | |
| $V=\dfrac{1}{6}$ | |
| $V=\dfrac{2}{3}$ |
Cho tứ diện $ABCD$, trên các cạnh $BC$, $BD$, $AC$ lần lượt lấy các điểm $M,\,N,\,P$ sao cho $BC=3BM$, $BD=\dfrac{3}{2}BN$, $AC=2AP$. Mặt phẳng $(MNP)$ chia khối tứ diện $ABCD$ thành hai khối đa diện có thể tích là $V_1$, $V_2$, trong đó khối đa diện chứa cạnh $CD$ có thể tích là $V_2$. Tính tỉ số $\dfrac{V_1}{V_2}$.
| $\dfrac{V_1}{V_2}=\dfrac{26}{19}$ | |
| $\dfrac{V_1}{V_2}=\dfrac{26}{13}$ | |
| $\dfrac{V_1}{V_2}=\dfrac{3}{19}$ | |
| $\dfrac{V_1}{V_2}=\dfrac{15}{19}$ |
Cho hình chóp $S.ABC$ có đáy là tam giác $ABC$ đều cạnh $a$. Hình chiếu của điểm $S$ trên mặt phẳng $(ABC)$ là điểm $H$ trên cạnh $AC$ thỏa mãn $AH=\dfrac{2}{3}AC$. Đường thẳng $SC$ tạo với mặt phẳng $(ABC)$ một góc bằng $60^\circ$. Thể tích của khối chóp $S.ABC$ bằng
| $\dfrac{a^3\sqrt{3}}{12}$ | |
| $\dfrac{a^3}{12}$ | |
| $\dfrac{a^3}{9}$ | |
| $\dfrac{a^3\sqrt{2}}{9}$ |
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật có cạnh $AB=a$, $BC=2a$. Hai mặt bên $(SAB)$ và $(SAD)$ cùng vuông góc với mặt phẳng đáy $(ABCD)$, cạnh bên $SA=a\sqrt{15}$. Tính theo $a$ thể tích $V$ của khối chóp $S.ABCD$.
| $V=\dfrac{2a^3\sqrt{15}}{6}$ | |
| $V=\dfrac{2a^3\sqrt{15}}{3}$ | |
| $V=2a^3\sqrt{15}$ | |
| $V=\dfrac{a^3\sqrt{15}}{3}$ |
Cho lăng trụ $ABCD.A'B'C'D'$ có đáy $ABCD$ là hình chữ nhật với $AB=\sqrt{6}$, $AD=\sqrt{3}$, $A'C=3$ và mặt phẳng $\left(AA'C'C\right)$ vuông góc với mặt đáy. Biết hai mặt phẳng $\left(AA'C'C\right)$, $\left(AA'B'B\right)$ tạo với nhau góc $\alpha$ thỏa mãn $\tan\alpha =\dfrac{3}{4}$. Thể tích khối lăng trụ $ABCD.A'B'C'D'$ bằng
| $V=6$ | |
| $V=8$ | |
| $V=12$ | |
| $V=10$ |
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều, cạnh \(a\). Cạnh bên \(SA=a\sqrt{3}\) và vuông góc với mặt đáy. Tính:
- Thể tích của khối chóp
- Khoảng cách từ điểm \(A\) đến mặt phẳng \((SBC)\).
Cho hình chóp tam giác $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $2a$ và $SA$ vuông góc với mặt phẳng $(ABC)$ (tham khảo hình vẽ).
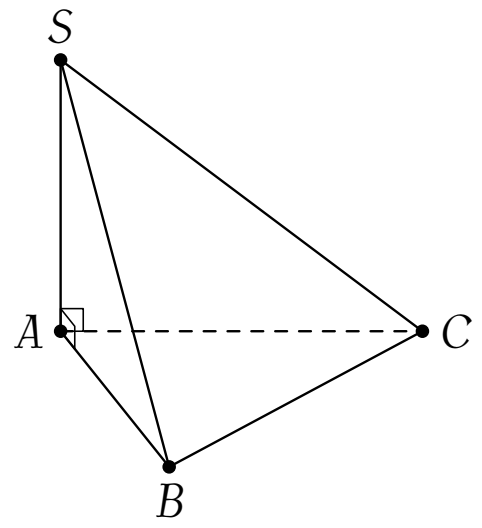
Biết thể tích của khối chóp $S.ABC$ là $\dfrac{a^3\sqrt{3}}{2}$ và góc giữa hai mặt phẳng $(SBC)$ và $(ABC)$ là góc nhọn $\alpha$. Chọn phát biểu đúng.
| $\alpha=60^{\circ}$ | |
| $\alpha=45^{\circ}$ | |
| $\alpha=30^{\circ}$ | |
| $\tan\alpha=\dfrac{\sqrt{3}}{2}$ |
Cho khối chóp $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $2a\sqrt{3}$ và $SA$ vuông góc với mặt phẳng $(ABC)$. Biết rằng thể tích của khối chóp $S.ABC$ bằng $\sqrt{3}a^3$. Tính độ dài cạnh $SA$.
| $2a\sqrt{3}$ | |
| $\sqrt{3}$ | |
| $2a$ | |
| $a$ |
Cho khối chóp $S.ABC$ có đáy là tam giác đều cạnh $2a$ và thể tích bằng $a^3$. Tính chiều cao $h$ của hình chóp đã cho.
| $h=\dfrac{\sqrt{3}a}{6}$ | |
| $h=\dfrac{\sqrt{3}a}{2}$ | |
| $h=\dfrac{\sqrt{3}a}{3}$ | |
| $h=\sqrt{3}a$ |
Cho khối chóp $S.ABC$ có đáy $ABC$ là tam giác đều, $SA$ vuông góc với mặt phẳng $(ABC)$ và $SA=a$. Biết rằng thể tích của khối chóp $S.ABC$ bằng $\sqrt{3}a^3$. Tính độ dài cạnh đáy của khối chóp $S.ABC$.
| $2a\sqrt{3}$ | |
| $3a\sqrt{3}$ | |
| $2a$ | |
| $2a\sqrt{2}$ |
