Cho hình vuông $ABCD$ tâm $O$. Gọi $M,\,N,\,P,\,Q$ lần lượt là trung điểm của các cạnh $AB$, $BC$, $CD$, $DA$.
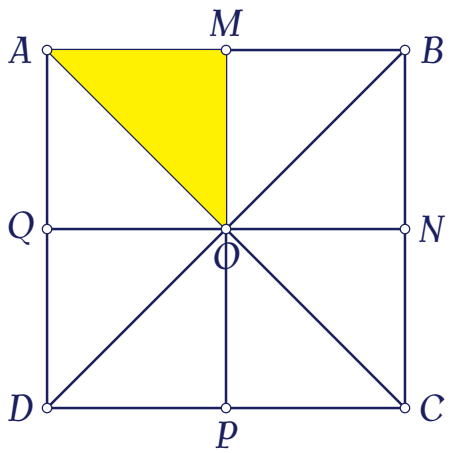
Ảnh của tam giác $OAM$ qua phép quay tâm $O$ góc $90^\circ$ là
 | $\triangle ODQ$ |
 | $\triangle OBN$ |
 | $\triangle OAQ$ |
 | $\triangle OCN$ |
Cho tam giác đều \(ABC\). Hãy xác định góc quay \(\varphi\) của phép quay tâm \(A\) biến điểm \(B\) thành điểm \(C\).
| \(\varphi=30^\circ\) |
| \(\varphi=90^\circ\) |
| \(\varphi=-120^\circ\) |
| \(\varphi=60^\circ\) hoặc \(\varphi=-60^\circ\) |
Cho hình vuông tâm \(O\). Với giá trị nào của \(\varphi\) thì phép quay \(\mathrm{Q}_{\left(O,\varphi\right)}\) biến hình vuông đã cho thành chính nó?
| \(\varphi=\dfrac{\pi}{6}\) |
| \(\varphi=\dfrac{\pi}{4}\) |
| \(\varphi=\dfrac{\pi}{3}\) |
| \(\varphi=\dfrac{\pi}{2}\) |
Cho tam giác đều tâm \(O\). Với giá trị nào của \(\varphi\) thì phép quay \(\mathrm{Q}_{\left(O,\varphi\right)}\) biến tam giác đều đã cho thành chính nó?
| \(\varphi=\dfrac{\pi}{3}\) |
| \(\varphi=\dfrac{2\pi}{3}\) |
| \(\varphi=\dfrac{3\pi}{2}\) |
| \(\varphi=\dfrac{\pi}{2}\) |
Trong mặt phẳng $Oxy$, phép quay tâm $O$ góc quay $-90^\circ$ biến $M(-3;5)$ thành điểm có tọa độ
| $(-5;-3)$ |
| $(5;-3)$ |
| $(5;3)$ |
| $(-5;3)$ |
Phép quay $\mathrm{Q}_{(O,\varphi)}$ biến đường tròn $(\mathscr{C})$ có bán kính $R$ thành đường tròn $(\mathscr{C}')$ có bán kính $R'$. Khẳng định nào sau đây đúng?
| $R'=3R$ |
| $R'=-3R$ |
| $R'=\dfrac{1}{3}R$ |
| $R'=R$ |
Trong mặt phẳng $Oxy$, cho điểm $A(1;0)$. Ảnh của $A$ qua phép quay tâm $O$ góc quay $90^\circ$ là
| $A’(0;-1)$ |
| $A’(-1;0)$ |
| $A’(0;1)$ |
| $A’(1;1)$ |
Cho phép quay $\mathrm{Q}_{(O,\varphi)}$ biến điểm $M$ thành $M'$. Khẳng định nào sau đây là khẳng định đúng?
| $\overrightarrow{OM}=\overrightarrow{OM'}$ và $\left(OM,OM'\right)=\varphi$ |
| $OM=OM'$ và $\left(OM,OM'\right)=\varphi$ |
| $\overrightarrow{OM}=\overrightarrow{OM'}$ và $\widehat{MOM'}=\varphi$ |
| $OM=OM'$ và $\widehat{MOM'}=\varphi$ |
Trong mặt phẳng $Oxy$, biết rằng phép quay tâm $O$ góc $\alpha$ là phép đồng nhất, tìm số đo của $\alpha$.
| $\alpha=k\pi\,(k\in\mathbb{Z})$ |
| $\alpha=k2\pi\,(k\in\mathbb{Z})$ |
| $\alpha=0$ |
| $\alpha=\dfrac{\pi}{2}$ |
Trong mặt phẳng $Oxy$, biểu thức tọa độ của phép quay $\mathrm{Q}_{\left(O,-\tfrac{\pi}{2}\right)}$ là
| $\begin{cases}x'=y\\ y'=x\end{cases}$ |
| $\begin{cases}x'=-y\\ y'=-x\end{cases}$ |
| $\begin{cases}x'=-y\\ y'=x\end{cases}$ |
| $\begin{cases}x'=y\\ y'=-x\end{cases}$ |
Trong mặt phẳng $Oxy$, biểu thức tọa độ của phép quay $\mathrm{Q}_{\left(O,\tfrac{\pi}{2}\right)}$ là
| $\begin{cases}x'=y\\ y'=-x\end{cases}$ |
| $\begin{cases}x'=-y\\ y'=-x\end{cases}$ |
| $\begin{cases}x'=-y\\ y'=x\end{cases}$ |
| $\begin{cases}x'=y\\ y'=x\end{cases}$ |
Trong mặt phẳng $Oxy$, biểu thức tọa độ của phép quay $\mathrm{Q}_{\left(O,\pi\right)}$ là
| $\begin{cases}x'=-x\\ y'=-y\end{cases}$ |
| $\begin{cases}x'=-x\\ y'=y\end{cases}$ |
| $\begin{cases}x'=x\\ y'=-y\end{cases}$ |
| $\begin{cases}x'=x\\ y'=y\end{cases}$ |
Trong mặt phẳng $Oxy$, cho điểm $I(a;b)$. Biểu thức tọa độ của phép quay $\mathrm{Q}_{\left(I,\varphi\right)}$ là
| $\begin{cases}x'=x\cos\varphi-y\sin\varphi\\ y'=x\sin\varphi+y\cos\varphi\end{cases}$ |
| $\begin{cases}x'=(x-a)\cos\varphi-(y-b)\sin\varphi\\ y'=(x-a)\sin\varphi+(y-b)\cos\varphi\end{cases}$ |
| $\begin{cases}x'=(x-a)\cos\varphi-(y-b)\sin\varphi-a\\ y'=(x-a)\sin\varphi+(y-b)\cos\varphi-b\end{cases}$ |
| $\begin{cases}x'=(x-a)\cos\varphi-(y-b)\sin\varphi+a\\ y'=(x-a)\sin\varphi+(y-b)\cos\varphi+b\end{cases}$ |
Biểu thức tọa độ của phép quay $\mathrm{Q}_{\left(O,\varphi\right)}$ là
| $\begin{cases}x'=x\cos\varphi-y\sin\varphi\\ y'=x\sin\varphi+y\cos\varphi\end{cases}$ |
| $\begin{cases}x'=x\cos\varphi+y\sin\varphi\\ y'=x\sin\varphi+y\cos\varphi\end{cases}$ |
| $\begin{cases}x'=x\cos\varphi+y\sin\varphi\\ y'=x\sin\varphi-y\cos\varphi\end{cases}$ |
| $\begin{cases}x'=x\sin\varphi-y\cos\varphi\\ y'=x\cos\varphi+y\sin\varphi\end{cases}$ |
Trong mặt phẳng $Oxy$, cho bốn điểm $A(-1;2)$, $B(3;-1)$, $A'(9;-4)$, $B'(5;-1)$. Phép quay tâm $I(a;b)$ biến điểm $A$ thành $A'$, điểm $B$ thành $B'$, khi đó giá trị $a+b$ bằng
| $5$ |
| $4$ |
| $3$ |
| $2$ |
Trong mặt phẳng $Oxy$, cho đường tròn $(\mathscr{C})\colon x^2+y^2-4x-2y=0$. Phép quay tâm $I$ góc $\dfrac{\pi}{4}$ biến $(\mathscr{C})$ thành chính nó. Tìm tọa độ tâm quay $I$.
| $I(0;0)$ |
| $I(2;1)$ |
| $I(1;2)$ |
| $I(1;1)$ |
Trong mặt phẳng $Oxy$, cho đường thẳng $d\colon3x-2y-1=0$. Ảnh của $d$ qua phép quay tâm $O$ góc $180^\circ$ có phương trình
| $3x+2y+1=0$ |
| $-3x+2y-1=0$ |
| $3x+2y-1=0$ |
| $3x-2y-1=0$ |
Trong mặt phẳng $Oxy$, điểm $M'(3;-2)$ là ảnh của điểm nào sau đây qua phép quay $Q_{(O,180^\circ)}$?
| $M(3;2)$ |
| $M(2;3)$ |
| $M(-3;2)$ |
| $M(-2;-3)$ |
Trong mặt phẳng $Oxy$, cho hai điểm $M(2;0)$ và $N(0;2)$. Phép quay tâm $O$ biến điểm $M$ thành điểm $N$, khi đó góc quay là
| $\alpha=30^\circ$ |
| $\alpha=90^\circ$ |
| $\alpha=30^\circ$ hoặc $\alpha=45^\circ$ |
| $\alpha=90^\circ$ hoặc $\alpha=270^\circ$ |
Trong mặt phẳng $Oxy$, cho các điểm $I(3;1)$ và $J(-1;-1)$. Tìm ảnh của $J$ qua phép quay $\mathrm{Q}_{(I,-90^\circ)}$.
| $J'(-3;3)$ |
| $J'(1;-5)$ |
| $J'(1;5)$ |
| $J'(5;-3)$ |