Cho hai đường thẳng $a$ và $b$ chéo nhau. Có bao nhiêu mặt phẳng chứa $a$ và song song với $b$?
| $0$ | |
| $1$ | |
| $2$ | |
| Vô số |
Trong các mệnh đề sau, mệnh đề nào đúng?
| Hai đường thẳng phân biệt không cắt nhau thì chéo nhau | |
| Hai đường thẳng phân biệt cùng nằm trong một mặt phẳng thì không chéo nhau | |
| Hai đường thẳng phân biệt không song song thì chéo nhau | |
| Hai đường thẳng phân biệt lần lượt thuộc hai mặt phẳng khác nhau thì chéo nhau |
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $a$, cạnh bên $SA=a$ và vuông góc với mặt đáy. Góc giữa đường thẳng $SC$ và mặt phẳng $(ABC)$ có số đo
| $45^\circ$ | |
| $90^\circ$ | |
| $30^\circ$ | |
| $60^\circ$ |
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $a$, cạnh bên $SA=a\sqrt{3}$ và vuông góc với mặt đáy. Góc giữa đường thẳng $SB$ và mặt phẳng $(ABC)$ có số đo
| $60^\circ$ | |
| $90^\circ$ | |
| $30^\circ$ | |
| $45^\circ$ |
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành tâm $I$ và $SA=SC$, $SB=SD$. Đường thẳng nào sau đây vuông góc với mặt phẳng $(ABCD)$?
| $SI$ | |
| $SA$ | |
| $SB$ | |
| $SC$ |
Cho hình chóp $S.ABC$ có $SA\perp AB$ và $SA\perp BC$. Khẳng định nào sau đây không đúng?
| $AB\perp BC$ | |
| $SA\perp AC$ | |
| $SA\perp(ABC)$ | |
| $\big(SA,(ABC)\big)=90^\circ$ |
Cho hình chóp $S.ABC$ có cạnh bên $SA$ vuông góc với mặt đáy. Góc giữa đường thẳng $SC$ và mặt phẳng $(ABC)$ là góc
| $\widehat{SCA}$ | |
| $\widehat{SCB}$ | |
| $\widehat{SAC}$ | |
| $\widehat{ASC}$ |
Cho hình chóp $S.ABC$ có cạnh bên $SA$ vuông góc với mặt đáy. Góc giữa đường thẳng $SB$ và mặt phẳng $(ABC)$ là góc
| $\widehat{SBA}$ | |
| $\widehat{SBC}$ | |
| $\widehat{SAB}$ | |
| $\widehat{ASB}$ |
Cho hình chóp $S.ABC$ có cạnh bên $SA$ vuông góc với mặt đáy. Hình chiếu vuông góc của $SC$ trên mặt phẳng $(ABC)$ là đường thẳng
| $AC$ | |
| $BC$ | |
| $AB$ | |
| $SC$ |
Cho hình chóp $S.ABC$ có cạnh bên $SA$ vuông góc với mặt đáy. Hình chiếu vuông góc của $SB$ trên mặt phẳng $(ABC)$ là đường thẳng
| $AB$ | |
| $BC$ | |
| $SB$ | |
| $AC$ |
Cho hình chóp $S.ABC$ có cạnh bên $SA$ vuông góc với mặt đáy. Góc giữa đường thẳng $SA$ và mặt phẳng $(ABC)$ có số đo là
| $90^\circ$ | |
| $0^\circ$ | |
| $180^\circ$ | |
| $90$ |
Cho hình chóp $S.ABC$ có cạnh bên $SA$ vuông góc với mặt đáy. Khẳng định nào sau đây không đúng?
| $SB\perp BC$ | |
| $SA\perp AB$ | |
| $SA\perp AC$ | |
| $SA\perp BC$ |
Biết rằng $b,\,c$ là hai đường thẳng cắt nhau và cùng nằm trong mặt phẳng $(\alpha)$. Nếu đường thẳng $a$ vuông góc với cả $b$ và $c$ thì
| $a\perp(\alpha)$ | |
| $a\parallel(\alpha)$ | |
| $a\subset(\alpha)$ | |
| $a,\,b,\,c$ đồng quy |
Biết rằng đường thẳng $a$ vuông góc với mặt phẳng $(\alpha)$ và đường thẳng $b$ nằm trên mặt phẳng $(\alpha)$. Kết luận nào sau đây là đúng?
| $a\perp b$ | |
| $a\parallel b$ | |
| $a,\,b$ chéo nhau | |
| $a,\,b$ cắt nhau |
Trong không gian, cho hai đường thẳng $d$ và $d'$ có vectơ chỉ phương lần lượt là $\overrightarrow{u}$ và $\overrightarrow{v}$. Biết rằng $\cos\big(\overrightarrow{u},\overrightarrow{v}\big)=-\dfrac{1}{2}$, góc giữa hai đường thẳng $d$ và $d$ bằng bao nhiêu độ?
| $60^{\circ}$ | |
| $30^{\circ}$ | |
| $120^{\circ}$ | |
| $150^{\circ}$ |
Cho tam giác $ABC$, lấy điểm $I$ trên cạnh $AC$ kéo dài (hình bên).

Mệnh đề nào sau đây là mệnh đề sai?
| $(ABC)\equiv(BIC)$ | |
| $A\in(ABC)$ | |
| $BI\in(ABC)$ | |
| $I\in(ABC)$ |
Trong các mệnh đề sau, mệnh đề nào sai?
| Có duy nhất một mặt phẳng đi qua hai đường thẳng mà hai đường thẳng này lần lượt nằm trên hai mặt phẳng cắt nhau | |
| Ba điểm không thẳng hàng cùng thuộc một mặt phẳng duy nhất | |
| Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng sẽ có một đường thẳng chung đi qua điểm chung ấy | |
| Có duy nhất một mặt phẳng đi qua hai đường thẳng cắt nhau cho trước |
Trong các mệnh đề sau mệnh đề nào sai?
| Hình biểu diễn phải giữ nguyên quan hệ thuộc giữa điểm và đường thẳng | |
| Dùng nét đứt để biểu diễn cho đường bị che khuất | |
| Hình biểu diễn của đường thẳng là đường thẳng | |
| Hình biểu diễn của hai đường cắt nhau có thể là hai đường song song nhau |
Cho tứ diện \(ABCD\). Gọi \(M,\,N\) lần lượt là trung điểm của các cạnh \(AD\) và \(BC\); \(G\) là trọng tâm tam giác \(BCD\).
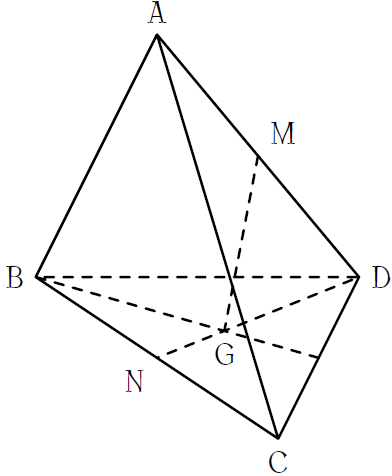
Khi ấy giao điểm của đường thẳng \(MG\) và mặt phẳng \((ABC)\) là
| Điểm \(C\) | |
| Điểm \(N\) | |
| Giao điểm của đường thẳng \(MG\) và đường thẳng \(BC\) | |
| Giao điểm của đường thẳng \(MG\) và đường thẳng \(AN\) |
Cho hai đường thẳng $a$ và $b$ cùng song song với $(P)$. Khẳng định nào sau đây là đúng?
| $a$ và $b$ chéo nhau | |
| Chưa đủ điều kiện để kết luận vị trí tương đối của $a$ và $b$ | |
| $a\parallel b$ | |
| $a$ và $b$ cắt nhau |
