Biết rằng đồ thị hàm số \(y=\dfrac{(m-2n-3)x+5}{x-m-n}\) nhận hai trục tọa độ làm hai đường tiệm cận. Tính tổng \(S=m^2+n^2-2\).
| \(S=2\) | |
| \(S=0\) | |
| \(S=-1\) | |
| \(S=1\) |
Cho hàm số $f(x)=\dfrac{ax-1}{bx+c}\,(a,\,b,\,c\in\mathbb{R})$ có bảng biến thiên như hình bên.
Giá trị của $a-b-c$ thuộc khoảnh nào sau đây?
| $\left(-1;0\right)$ | |
| $\left(-2;-1\right)$ | |
| $\left(1;2\right)$ | |
| $\left(0;1\right)$ |
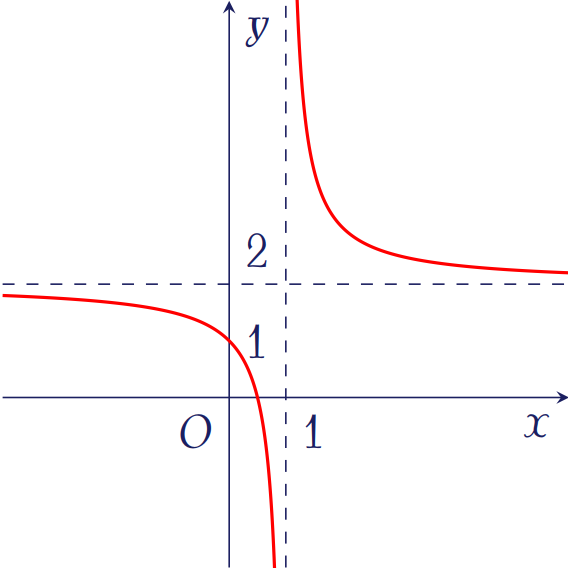
Cho hàm số \(y=\dfrac{ax-1}{bx+c}\) có đồ thị như hình trên. Tính giá trị biểu thức \(T=a+2b+3c\).
| \(T=1\) | |
| \(T=2\) | |
| \(T=3\) | |
| \(T=4\) |
Biết rằng đồ thị hàm số \(y=\dfrac{ax+1}{bx-2}\) có đường tiệm cận đứng là \(x=2\) và đường tiệm cận ngang là \(y=3\). Tính giá trị của \(a+b\).
| \(a+b=1\) | |
| \(a+b=5\) | |
| \(a+b=4\) | |
| \(a+b=0\) |
Đường tiệm cận ngang của đồ thị hàm số $y=\dfrac{3x-4}{x-1}$ là
| $x=3$ | |
| $y=1$ | |
| $x=1$ | |
| $y=3$ |
Tiệm cận đứng của đồ thị hàm số $y=\dfrac{3x-2}{x+4}$ là đường thẳng có phương trình
| $x=4$ | |
| $x=3$ | |
| $x=-3$ | |
| $x=-4$ |
Cho hàm số $y=\dfrac{ax+b}{cx+1}$ ($a,\,b,\,c\in\mathbb{R}$) có đồ thị như hình bên.
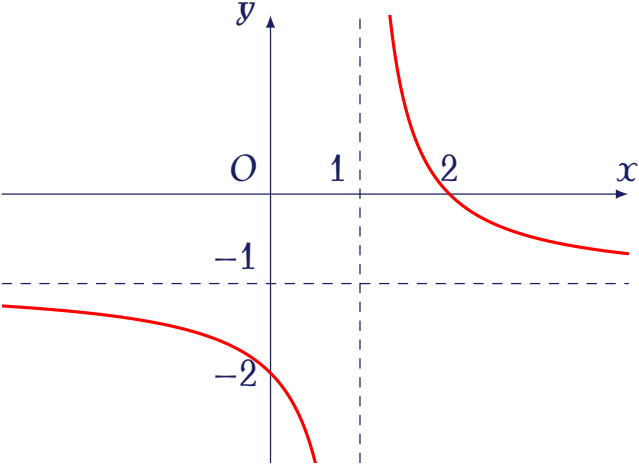
Khi đó $a+b-c$ bằng
| $-2$ | |
| $-1$ | |
| $1$ | |
| $0$ |
Giá trị của tham số $m$ sao cho tiệm cận ngang của đồ thị hàm số $y=\dfrac{mx+5}{x+1}$ đi qua điểm $M(2;-4)$ là
| $4$ | |
| $-4$ | |
| $-2$ | |
| $2$ |
Tiệm cận ngang của đồ thị hàm số $y=\dfrac{x+2022}{x+1}$ là
| $y=2022$ | |
| $y=-1$ | |
| $y=1$ | |
| $y=-2022$ |
Tiệm cận đứng của đồ thị hàm số $y=\dfrac{3x-1}{x-2}$ có phương trình là
| $x=2$ | |
| $x=-2$ | |
| $x=3$ | |
| $x=\dfrac{1}{2}$ |
Tiệm cận đứng của đồ thị hàm số $y=\dfrac{2x-1}{x+1}$ là đường thẳng có phương trình
| $y=-1$ | |
| $x=-1$ | |
| $y=2$ | |
| $x=2$ |
Tiệm cận ngang của đồ thị hàm số $y=\dfrac{2x+1}{3x-1}$ là đường thẳng có phương trình
| $y=\dfrac{1}{3}$ | |
| $y=-\dfrac{2}{3}$ | |
| $y=-\dfrac{1}{3}$ | |
| $y=\dfrac{2}{3}$ |
Cho hàm số $y=\dfrac{-x+1}{2x-1}$ có đồ thị $(\mathscr{C})$ và đường thẳng $(d)\colon y=x+m$. Với mọi giá trị thực của $m$ đường thẳng $(d)$ luôn cắt đồ thị $(\mathscr{C})$ tại hai điểm phân biệt $A$ và $B$. Gọi $k_1,\,k_2$ lần lượt là hệ số góc của các tiếp tuyến với $(\mathscr{C})$ tại $A$ và $B$. Giá trị nhỏ nhất của $T=k_1^{2022}+k_2^{2022}$ bằng
| $\dfrac{1}{2}$ | |
| $2$ | |
| $\dfrac{2}{3}$ | |
| $1$ |
Có bao nhiêu giá trị nguyên thuộc đoạn $[-10;10]$ của $m$ để giá trị lớn nhất của hàm số $y=\dfrac{2x+m}{x+1}$ trên đoạn $[-4;-2]$ không lớn hơn $1$?
| $6$ | |
| $7$ | |
| $8$ | |
| $5$ |
Tiệm cận đứng của đồ thị hàm số $y=\dfrac{2x-1}{x-3}$ là đường thẳng có phương trình
| $x=\dfrac{1}{2}$ | |
| $x=\dfrac{1}{3}$ | |
| $x=2$ | |
| $x=3$ |
Tiệm cận đứng của đồ thị hàm số $y=\dfrac{3x-2}{x+4}$ là đường thẳng có phương trình
| $x=4$ | |
| $x=3$ | |
| $x=-3$ | |
| $x=-4$ |
Cho hàm số $y=\dfrac{ax+b}{cx+1}$ ($a,b,c\in\mathbb{R}$) có đồ thị như hình bên.
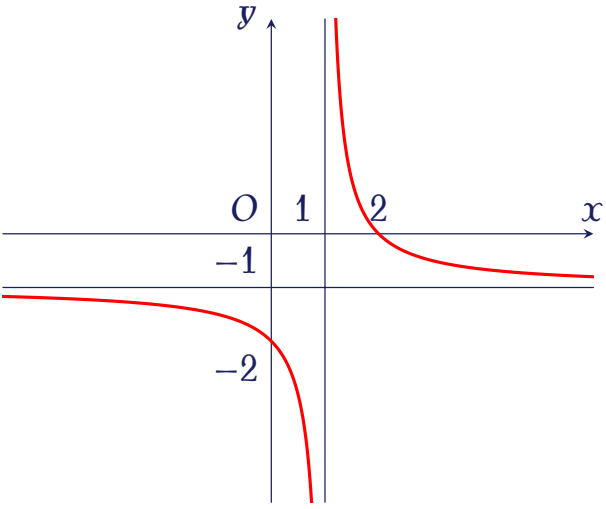
Khi đó $a+b-c$ bằng
| $-2$ | |
| $-1$ | |
| $1$ | |
| $0$ |
Tiệm cận ngang của đồ thị hàm số $y=\dfrac{2x-1}{2x+4}$ là đường thẳng có phương trình
| $x=-2$ | |
| $x=1$ | |
| $y=1$ | |
| $y=-2$ |
Cho hàm số $y=\dfrac{x}{x-1}+2$ có đồ thị $\left(\mathscr{C}\right)$ Mệnh đề nào dưới đây đúng?
| Đồ thị $\left(\mathscr{C}\right)$ có tiệm cận ngang $y=1$ | |
| Đồ thị $\left(\mathscr{C}\right)$ có tiệm cận ngang $y=3$ | |
| Đồ thị $\left(\mathscr{C}\right)$ không có tiệm cận | |
| Đồ thị $\left(\mathscr{C}\right)$ có tiệm cận đứng $x=2$ |
Tìm tất cả các giá trị thực của tham số $m$ sao cho đồ thị hàm số $y=\dfrac{2x-\sqrt{mx^2+1}}{x-1}$ có đúng hai đường tiệm cận ngang.
| $m<0$ | |
| $0<m<3$ hoặc $m>3$ | |
| $m>0$ | |
| $m=0$ |
