Tìm giá trị nhỏ nhất của tham số $m$ để bất phương trình $$\dfrac{x^3+\sqrt{3x^2+1}+1}{\sqrt{x}-\sqrt{x-1}}\leq\dfrac{m}{\left(\sqrt{x}+\sqrt{x-1}\right)^2}$$có nghiệm.
| $m=1$ | |
| $m=4$ | |
| $m=13$ | |
| $m=8$ |
Tìm $m$ sao cho bất phương trình $\dfrac{x^2-2x+2}{x-1}\leq m$ có đúng một nghiệm trên khoảng $(1;+\infty)$.
| $m\geq2$ | |
| $m\leq2$ | |
| $m=2$ | |
| $m>2$ |
Cho hàm số $f\left(x\right)=x^3-2x^2+mx-3$ . Tìm $m$ để $f'\left(x\right)< 0$ với mọi $x\in\left(0;2\right)$.
Có bao nhiêu số nguyên $a$ sao cho ứng với mỗi $a$, tồn tại ít nhất bốn số nguyên $b\in(-12;12)$ thỏa mãn $4^{a^2+b}\leq3^{b-a}+65$?
| $4$ | |
| $6$ | |
| $5$ | |
| $7$ |
Cho số phức $z=m+1+mi$ với $m\in\mathbb{R}$. Hỏi có bao nhiêu giá trị nguyên của $m\in(-5;5)$ sao cho $|z-2i|>1$?
| $0$ | |
| $4$ | |
| $5$ | |
| $9$ |
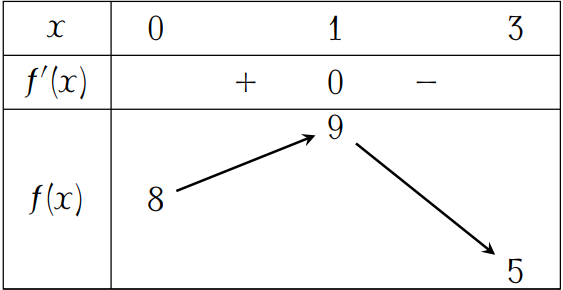
Cho hàm số \(y=f(x)\) có bảng biến thiên như hình. Gọi \(S\) là tập hợp các số nguyên dương \(m\) để bất phương trình $$f(x)\geq mx^2\left(x^2-2\right)+2m$$có nghiệm thuộc đoạn \([0;3]\). Số phần tử của tập \(S\) là
| \(9\) | |
| \(10\) | |
| Vô số | |
| \(0\) |
Tìm \(m\) để bất phương trình \(x+\dfrac{4}{x-1}\geq m\) có nghiệm trên khoảng \((-\infty;1)\).
| \(m\leq3\) | |
| \(m\leq-3\) | |
| \(m\leq5\) | |
| \(m\leq-1\) |
Có bao nhiêu giá trị nguyên của tham số $m\in(-10;100)$ để tồn tại các số thực dương $a,\,b,\,x,\,y$ thỏa mãn $a\neq1$, $b\neq1$ và $a^{2x}=b^y=(ab)^{x+my}$?
| $0$ | |
| $100$ | |
| $99$ | |
| $98$ |
Gọi $S$ là tập hợp các giá trị nguyên của $y$ sao cho ứng với mỗi $y$, tồn tại duy nhất một giá trị $x\in\left[\dfrac{3}{2};\dfrac{9}{2}\right]$ thỏa mãn $\log_3\big(x^3-6x^2+9x+y\big)=\log_2\big(-x^2+6x-5\big)$. Số phần tử của $S$ là
| $7$ | |
| $1$ | |
| $8$ | |
| $3$ |
Có bao nhiêu giá trị nguyên của tham số a thuộc đoạn $[-10;10]$ để hàm số $$y=\big|-x^3+3(a+1)x^2-3a(a+2)x+a^2(a+3)\big|$$đồng biến trên khoảng $(0;1)$
| $21$ | |
| $10$ | |
| $8$ | |
| $2$ |
Có bao nhiêu giá trị nguyên của tham số $a\in(-10;+\infty)$ để hàm số $y=\big|x^3+(a+2)x+9-a^2\big|$ đồng biến trên khoảng $(0;1)$?
| $12$ | |
| $11$ | |
| $6$ | |
| $5$ |
Có bao nhiêu số nguyên $y$ sao cho tồn tại $x\in\left(\dfrac{1}{3};3\right)$ thỏa mãn $27^{3x^2+xy}=(1+xy)\cdot27^{9x}$?
| $27$ | |
| $9$ | |
| $11$ | |
| $12$ |
Cho hàm số $$y=2x^3-3(3m+1)x^2+6\left(2m^2+m\right)x-12m^2+3m+1.$$Tính tổng tất cả giá trị nguyên dương của tham số \(m\) để hàm số nghịch biến trên khoảng \((1;3)\).
| \(0\) | |
| \(3\) | |
| \(1\) | |
| \(2\) |
Cho hai số thực $x,\,y$ bất kì. Khẳng định nào dưới đây đúng?
| $5^x< 5^y\Leftrightarrow x>y$ | |
| $5^x>5^y\Leftrightarrow x>y$ | |
| $5^x>5^y\Leftrightarrow x< y$ | |
| $5^x>5^y\Leftrightarrow x=y$ |
Tập nghiệm của bất phương trình $3^x>5$ là
| $\big(0;\log_35\big)$ | |
| $\big(\log_53;+\infty\big)$ | |
| $\big(\log_35;+\infty\big)$ | |
| $\big(0;\log_53\big)$ |
Có bao nhiêu số nguyên $y\in(-2022;2022]$ để bất phương trình $2+\log_{\sqrt{3}}(y-1)\leq\log_{\sqrt{3}}\big[x^2-2(3+y)x+2y^2+24\big]$ nghiệm đúng với mọi $x\in\mathbb{R}$?
| $2011$ | |
| $2021$ | |
| $2019$ | |
| $4041$ |
Tập nghiệm của bất phương trình $3^x\leq81$ là
| $(-\infty;4]$ | |
| $[4;+\infty)$ | |
| $(4;+\infty)$ | |
| $(-\infty;4)$ |
Có bao nhiêu số nguyên $x$ thoả mãn $\big(7^x-49\big)\big(\log_3^2x-7\log_3x+6\big)< 0$?
| $728$ | |
| $726$ | |
| $725$ | |
| $729$ |
Tập nghiệm của bất phương trình $2^{2x}< 8$ là
| $\left(-\infty;\dfrac{3}{2}\right)$ | |
| $\left(\dfrac{3}{2};+\infty\right)$ | |
| $(-\infty;2)$ | |
| $\left(0;\dfrac{3}{2}\right)$ |
Có bao nhiêu số nguyên dương $x$ sao cho tồn tại số thực $y$ lớn hơn $1$ thỏa mãn $\big(xy^2+x-2y-1)\log y=\log\dfrac{2y-x+3}{x}$?
| $3$ | |
| $1$ | |
| Vô số | |
| $2$ |
