Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thang, đáy lớn $AB$. Phát biểu nào không đúng về giao tuyến của hai mặt phẳng $(SAB)$ và $(SCD)$?

	Song song với $CD$
	Đi qua điểm $S$
	Song song với $AB$
	Đi qua giao điểm $I$ của $AB$ và $CD$

Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thang, đáy lớn $AB$. Giao tuyến của hai mặt phẳng $(SAB)$ và $(SCD)$

	Không tồn tại
	Đi qua điểm $S$
	Đi qua giao điểm $I$ của $AD$ và $BC$
	Đi qua giao điểm $I$ của $AB$ và $CD$

Cho hình chóp $S.ABCD$ có đáy là hình thang $ABCD$ ($AB\parallel CD$). Khẳng định nào sau đây sai?

	$S.ABCD$ có $4$ mặt bên
	Giao tuyến của $(SAC)$ và $(SBD)$ là $SO$, với $O=AC\cap BD$
	Giao tuyến của $(SAD)$ và $(SBC)$ là $SI$, với $I=AD\cap BC$
	Giao tuyến của $(SAB)$ và $(SAD)$ là $BD$

Cho hình chóp tứ giác $S.ABCD$. Gọi $M$ và $N$ lần lượt là trung điểm của $SA$ và $SC$. Khẳng định nào sau đây đúng?

	$MN\parallel(ABCD)$
	$MN\parallel(SAB)$
	$MN\parallel(SCD)$
	$MN\parallel(SBC)$

Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành. Gọi $M,\,N$ lần lượt là trung điểm $AD$ và $BC$. Giao tuyến của hai mặt phẳng $(SMN)$ và $(SAC)$ là

	$SD$
	$SO$ ($O$ là tâm của hình bình hành $ABCD$)
	$SG$ ($G$ là trung điểm cạnh $AB$)
	$SF$ ($F$ là trung điểm cạnh $CD$)

Cho $S$ là một điểm không thuộc mặt hình thang $ABCD$ ($AB\parallel CD$ và $AB>CD$). Gọi $I$ là giao điểm của $AD$ và $BC$. Khi đó giao tuyến của hai mặt phẳng $(SAD)$ và $(SCB)$ là

	$BI$
	$SD$
	$SC$
	$SI$

Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành. Gọi $d$ là giao tuyến của hai mặt phẳng $(SAD)$ và $(SBC)$. Khẳng định nào sau đây đúng?

	$d$ qua $S$ và song song với $BC$
	$d$ qua $S$ và song song với $DC$
	$d$ qua $S$ và song song với $AB$
	$d$ qua $S$ và song song với $BD$

Cho hình chóp $S.ABCD$ có đáy là tứ giác lồi. Hai điểm $G$, $H$ lần lượt là trọng tâm của $\triangle SAB$ và $\triangle SCD$. Tìm giao tuyến của các cặp mặt phẳng sau:

1. $(SGH)$ và $(ABCD)$.
2. $(SAC)$ và $(SGH)$.
3. $(SAC)$ và $(BGH)$.
4. $(SCD)$ và $(BGH)$.

Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành. Gọi $M$, $N$, $P$ lần lượt là trung điểm các cạnh $BC$, $CD$, $SA$. Tìm giao tuyến của các cặp mặt phẳng sau:

1. $(SAC)$ và $(SBD)$.
2. $(MNP)$ và $(SAB)$.
3. $(MNP)$ và $(SAD)$.
4. $(MNP)$ và $(SBC)$.
5. $(MNP)$ và $(SCD)$.

Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành tâm $O$. Lấy điểm $M$ trên cạnh $SA$, trung điểm $CD$ là $N$. Tìm giao tuyến của các cặp mặt phẳng sau:

1. $(SAC)$ và $(SBD)$.
2. $(BMN)$ và $(SAD)$.
3. $(BMN)$ và $(SAC)$.
4. $(MCD)$ và $(SBD)$.
5. $(MCD)$ và $(SAB)$.

Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành tâm $I$ và $SA=SC$, $SB=SD$. Đường thẳng nào sau đây vuông góc với mặt phẳng $(ABCD)$?

	$SI$
	$SA$
	$SB$
	$SC$

Cho hình chóp đều $S.ABCD$ có chiều cao $a$, $AC=2a$ (tham khảo hình bên).

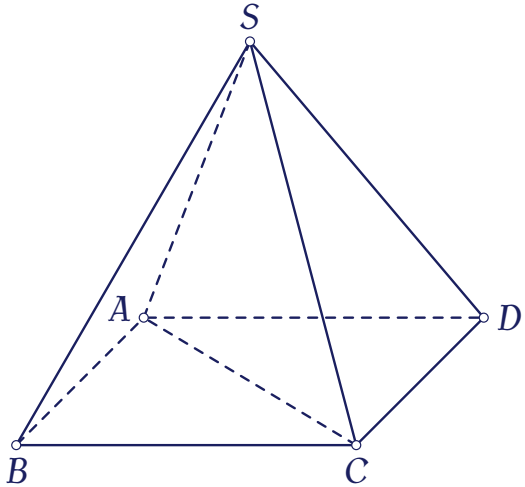
Khoảng cách từ $B$ đến mặt phẳng $(SCD)$ bằng

	$\dfrac{\sqrt{3}}{3}a$
	$\sqrt{2}a$
	$\dfrac{2\sqrt{3}}{3}a$
	$\dfrac{\sqrt{2}}{2}a$

Cho hình chóp $S.ABC$. Gọi $M,\,N,\,P$ lần lượt là trung điểm của $SA,\,SB,\,SC$. Chọn khẳng định đúng.

	$(MNP)\parallel(ABC)$
	$(MNP)\parallel(SAC)$
	$(SMN)\parallel(ABC)$
	$(MNP)\parallel(SBC)$

Cho hình chóp $S.ABCD$ có $ABCD$ là hình vuông cạnh $2a$, $SA\perp(ABCD)$ và $2a\sqrt{2}$.

1. Chứng minh rằng $BD\perp(SAC)$.
2. Tính góc tạo bởi $SC$ và $(SAD)$.

Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông và $SA\perp(ABCD)$.

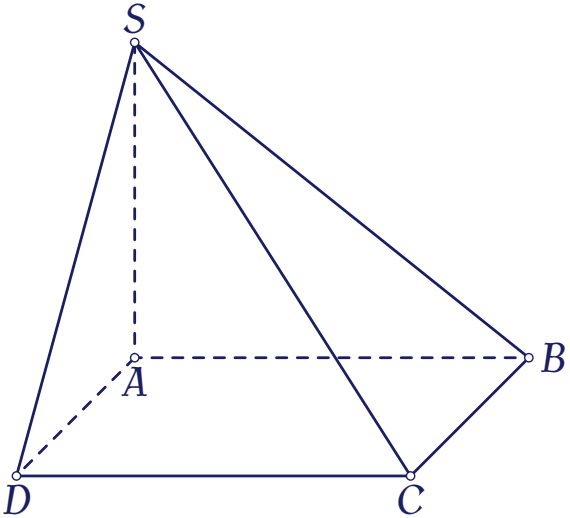
Khẳng định nào sau đây là đúng?

	$BC\perp(SAB)$
	$BC\perp(SBD)$
	$BC\perp(SCD)$
	$BC\perp(SAC)$

Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông, $SA$ vuông góc mặt đáy. Hình chiếu vuông góc của $SB$ lên $(ABCD)$ là

	$CB$
	$DB$
	$AB$
	$SA$

Cho tứ diện $ABCD$ và điểm $M$ thuộc miền trong của tam giác $ACD$. Gọi $I,\,J$ lần lượt là hai điểm trên cạnh $BC$ và $BD$ sao cho $IJ$ không song song với $CD$. Gọi $H$ là giao điểm của $IJ$ với $CD$, $K$ là giao điểm của $MH$ với $AC$. Giao tuyến của hai mặt phẳng $(ACD)$ và $(IJM)$ là

	$KI$
	$KJ$
	$MI$
	$MH$

Cho $4$ điểm không đồng phẳng $A,\,B,\,C,\,D$. Gọi $I,\,K$ lần lượt là trung điểm của $AD$ và $BC$. Giao tuyến của $(IBC)$ và $(KAD)$ là

	$IK$
	$BC$
	$AK$
	$DK$

Cho tứ diện $ABCD$. Gọi $G$ là trọng tâm của tam giác $BCD$. Giao tuyến của hai mặt phẳng $(ACD)$ và $(GAB)$ là

	$AM$ ($M$ là trung điểm của $AB$)
	$AN$ ($N$ là trung điểm của $CD$)
	$AH$ ($H$ là hình chiếu của $B$ trên $CD$)
	$AK$ ($K$ là hình chiếu của $C$ trên $BD$)

Trong mặt phẳng $(\alpha)$, cho bốn điểm $A,\,B,\,C,\,D$ trong đó không có ba điểm nào thẳng hàng. Điểm $S$ không thuộc mặt phẳng $(\alpha)$. Có bao nhiêu mặt phẳng tạo bởi $S$ và $2$ trong $4$ điểm nói trên?

	$4$
	$5$
	$6$
	$8$