Cho hàm số $y=\big(2x^2-1\big)^{\tfrac{1}{2}}$. Giá trị của hàm số đã cho tại điểm $x=2$ bằng
| $3$ | |
| $\sqrt{7}$ | |
| $\sqrt{3}$ | |
| $7$ |
Tập xác định của hàm số $y=x^{\sqrt{2}-1}$ là
| $\big(-\infty;\sqrt{2}\big)$ | |
| $\mathbb{R}\setminus\{0\}$ | |
| $\mathbb{R}$ | |
| $(0;+\infty)$ |
Đạo hàm của hàm số $y=x^{2023}$ là
| $y'=2023x^{2023}$ | |
| $y'=2022x^{2023}$ | |
| $y'=2023x^{2022}$ | |
| $y'=\dfrac{1}{2023}x^{2022}$ |
Biết đồ thị của hàm số $f(x)=ax^3+bx^2+cx+d$ có hai điểm cực trị là $A(1;1)$ và $B\left(2;\dfrac{4}{3}\right)$. Tính $f(-1)$.
| $12$ | |
| $7$ | |
| $\dfrac{31}{3}$ | |
| $\dfrac{16}{3}$ |
Đạo hàm của hàm số $y=\big(x^4+3\big)^{\tfrac{1}{3}}$ là
| $y'=\dfrac{4}{3}x^3\big(x^4+3\big)^{-\tfrac{2}{3}}$ | |
| $y'=\dfrac{1}{3}x^3\big(x^4+3\big)^{-\tfrac{2}{3}}$ | |
| $y'=\dfrac{4}{3}x^3\big(x^4+3\big)^{\tfrac{2}{3}}$ | |
| $y'=4x^3\big(x^4+3\big)^{-\tfrac{2}{3}}$ |
Đạo hàm của hàm số $y=(x+1)^\pi$ là
| $y'=\pi(x+1)^\pi$ | |
| $y'=(\pi-1)(x+1)^{\pi-1}$ | |
| $y'=\pi(x+1)^{\pi-1}$ | |
| $y'=(x+1)^{\pi-1}$ |
Trên khoảng $(0;+\infty)$, đạo hàm của hàm số $y=x^{\pi}$ là
| $y'=\pi x^{\pi-1}$ | |
| $y'=x^{\pi-1}$ | |
| $y'=\dfrac{1}{\pi}x^{\pi-1}$ | |
| $y'=\pi x^{\pi}$ |
Tập xác định của hàm số $y=(x+2)^{-2022}$ là
| $[-2;+\infty)$ | |
| $(-2;+\infty)$ | |
| $\mathbb{R}\setminus\{-2\}$ | |
| $\mathbb{R}$ |
Cho đồ thị các hàm số $y=x^\alpha$ và $y=x^\beta$ trên khoảng $(0;+\infty)$.
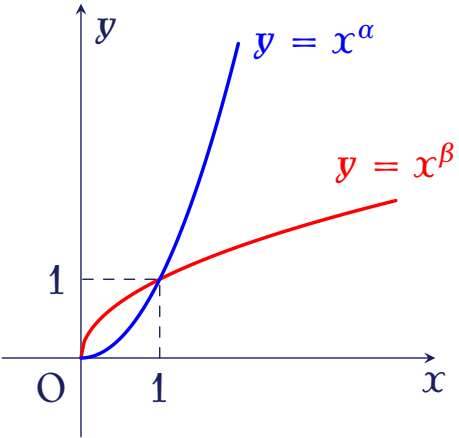
Mệnh đề nào dưới đây đúng?
| $0< \alpha< 1< \beta$ | |
| $\alpha< 0< 1< \beta$ | |
| $0< \beta< 1< \alpha$ | |
| $\beta< 0< 1< \alpha$ |
Biết đồ thị của hàm số $f(x)=ax^3+bx^2+cx+d$ có hai điểm cực trị là $A(1;1)$ và $B\left(2;\dfrac{4}{3}\right)$. Tính $f(-1)$.
| $12$ | |
| $7$ | |
| $\dfrac{31}{3}$ | |
| $\dfrac{16}{3}$ |
Đạo hàm của hàm số $y=\big(x^4+3\big)^{\tfrac{1}{3}}$ là
| $y'=\dfrac{4}{3}x^3\big(x^4+3\big)^{-\tfrac{2}{3}}$ | |
| $y'=\dfrac{1}{3}x^3\big(x^4+3\big)^{-\tfrac{2}{3}}$ | |
| $y'=\dfrac{4}{3}x^3\big(x^4+3\big)^{\tfrac{2}{3}}$ | |
| $y'=4x^3\big(x^4+3\big)^{-\tfrac{2}{3}}$ |
Đạo hàm của hàm số $y=x^{-3}$ là
| $y'=-x^{-4}$ | |
| $y'=-\dfrac{1}{2}x^{-2}$ | |
| $y'=-\dfrac{1}{3}x^{-4}$ | |
| $y'=-3x^{-4}$ |
Tập xác định của hàm số $y=x^{-\pi}$ là
| $\left(-\infty;0\right)$ | |
| $\mathbb{R}\setminus\{0\}$ | |
| $\left[0;+\infty\right)$ | |
| $\left(0;+\infty\right)$ |
Cho hàm số $f(x)=\begin{cases}2x+5 &\text{khi }x\ge1\\ 3x^2+4 &\text{khi }x< 1\end{cases}$. Giả sử $F$ là nguyên hàm của $f$ trên $\mathbb{R}$ thỏa mãn $F(0)=2$. Giá trị của $F(-1)+2F(2)$ bằng
| $27$ | |
| $29$ | |
| $12$ | |
| $33$ |
Trên khoảng $(0;+\infty)$, đạo hàm của hàm số $y=x^{\tfrac{5}{2}}$ là
| $y'=\dfrac{2}{7}x^{\tfrac{7}{2}}$ | |
| $y'=\dfrac{2}{5}x^{\tfrac{3}{2}}$ | |
| $y'=\dfrac{5}{2}x^{\tfrac{3}{2}}$ | |
| $y'=\dfrac{5}{2}x^{-\tfrac{3}{2}}$ |
Cho hàm số $f(x)$ xác định trên $\mathbb{R}\setminus\{1\}$ thỏa mãn $f^{\prime}(x)=\dfrac{1}{x-1}$, $f(3)=2021$. Tính $f(5)$.
| $f(5)=2020-\dfrac{1}{2}\ln2$ | |
| $f(5)=2021-\ln2$ | |
| $f(5)=2021+\ln2$ | |
| $f(5)=2020+\ln2$ |
Cho hàm số $y=f(x)$ có đạo hàm là $f^{\prime}(x)=12x^2+2$, $\forall x\in\mathbb{R}$ và $f(1)=3$. Biết $F(x)$ là nguyên hàm của $f(x)$ thỏa mãn $F(0)=2$, khi đó $F(1)$ bằng
| $-3$ | |
| $1$ | |
| $2$ | |
| $7$ |
Tập xác định của hàm số $y=x^{\sqrt{2}}$ là
| $\mathbb{R}$ | |
| $\mathbb{R}\setminus\{0\}$ | |
| $(0;+\infty)$ | |
| $(2;+\infty)$ |
Trên khoảng $(0;+\infty)$, họ nguyên hàm của hàm số $f(x)=x^{\tfrac{3}{2}}$ là
| $\displaystyle\displaystyle\int f(x)\mathrm{\,d}x=\dfrac{3}{2}x^{\tfrac{1}{2}}+C$ | |
| $\displaystyle\displaystyle\int f(x)\mathrm{\,d}x=\dfrac{5}{2}x^{\tfrac{2}{5}}+C$ | |
| $\displaystyle\displaystyle\int f(x)\mathrm{\,d}x=\dfrac{2}{5}x^{\tfrac{5}{2}}+C$ | |
| $\displaystyle\displaystyle\int f(x)\mathrm{\,d}x=\dfrac{2}{3}x^{\tfrac{1}{2}}+C$ |
Cho hàm số $f(x)$ liên tục trên $\mathbb{R}$ thỏa $f(x)=\sin x+2\displaystyle\int\limits_{0}^{\tfrac{\pi}{2}}\cos x\cdot f(x)\mathrm{\,d}x$. Giá trị $f\left(-\dfrac{\pi}{2}\right)$ bằng
| $-\pi$ | |
| $-1$ | |
| $-2$ | |
| $0$ |
