Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $a$, cạnh bên $SA=a$ và vuông góc với mặt đáy. Góc giữa đường thẳng $SC$ và mặt phẳng $(ABC)$ có số đo
| $45^\circ$ | |
| $90^\circ$ | |
| $30^\circ$ | |
| $60^\circ$ |
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $a$, cạnh bên $SA=a\sqrt{3}$ và vuông góc với mặt đáy. Góc giữa đường thẳng $SB$ và mặt phẳng $(ABC)$ có số đo
| $60^\circ$ | |
| $90^\circ$ | |
| $30^\circ$ | |
| $45^\circ$ |
Cho hình chóp $S.ABC$ có $SA\perp AB$ và $SA\perp BC$. Khẳng định nào sau đây không đúng?
| $AB\perp BC$ | |
| $SA\perp AC$ | |
| $SA\perp(ABC)$ | |
| $\big(SA,(ABC)\big)=90^\circ$ |
Cho hình chóp $S.ABC$ có cạnh bên $SA$ vuông góc với mặt đáy. Góc giữa đường thẳng $SC$ và mặt phẳng $(ABC)$ là góc
| $\widehat{SCA}$ | |
| $\widehat{SCB}$ | |
| $\widehat{SAC}$ | |
| $\widehat{ASC}$ |
Cho hình chóp $S.ABC$ có cạnh bên $SA$ vuông góc với mặt đáy. Góc giữa đường thẳng $SB$ và mặt phẳng $(ABC)$ là góc
| $\widehat{SBA}$ | |
| $\widehat{SBC}$ | |
| $\widehat{SAB}$ | |
| $\widehat{ASB}$ |
Cho hình chóp $S.ABC$ có cạnh bên $SA$ vuông góc với mặt đáy. Góc giữa đường thẳng $SA$ và mặt phẳng $(ABC)$ có số đo là
| $90^\circ$ | |
| $0^\circ$ | |
| $180^\circ$ | |
| $90$ |
Cho hình lập phương $ABCD.A'B'C'D'$. Tính góc giữa 2 vectơ $\overrightarrow{AB},\,\overrightarrow{A'C'}$.
| $\big(\overrightarrow{AB},\overrightarrow{A'C'}\big)=45^\circ$ | |
| $\big(\overrightarrow{AB},\overrightarrow{A'C'}\big)=60^\circ$ | |
| $\big(\overrightarrow{AB},\overrightarrow{A'C'}\big)=30^\circ$ | |
| $\big(\overrightarrow{AB},\overrightarrow{A'C'}\big)=90^\circ$ |
Cho 2 vectơ $\overrightarrow{u}=\overrightarrow{AB}$, $\overrightarrow{v}=\overrightarrow{AC}$. Khi đó $\big(\overrightarrow{u},\overrightarrow{v}\big)$ bằng
| $\widehat{ABC}$ | |
| $90^\circ$ | |
| $\widehat{ACB}$ | |
| $\widehat{BAC}$ |
Cho hình lập phương $ABCD.A'B'C'D'$. Tính góc giữa 2 đường thẳng $AC$ và $B'C$.
| $30^\circ$ | |
| $45^\circ$ | |
| $60^\circ$ | |
| $90^\circ$ |
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $a$, $SA\perp(ABC)$ và $SA=a$.
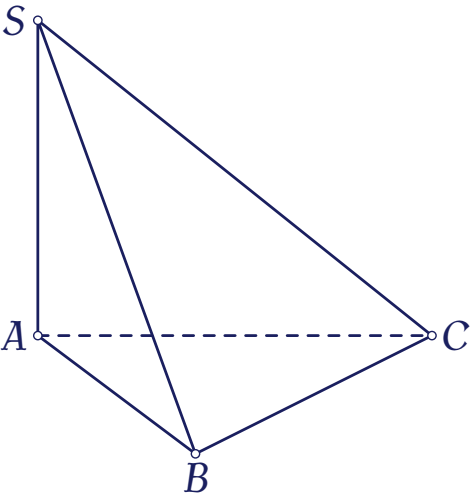
Góc giữa $SB$ và $AB$ bằng
| $60^{\circ}$ | |
| $90^{\circ}$ | |
| $135^{\circ}$ | |
| $45^{\circ}$ |
Trong không gian \(Oxyz\), cho mặt phẳng \((P)\colon x+y-z-1=0\) và điểm \(A(1;0;0)\in(P)\). Đường thẳng \(\Delta\) đi qua \(A\) nằm trong \((P)\) và tạo với trục \(Oz\) một góc nhỏ nhất. Gọi \(M\left(x_0;y_0;z_0\right)\) là giao điểm của đường thẳng \(\Delta\) với mặt phẳng \((Q)\colon2x+y-2z+1=0\). Tổng \(S=x_0+y_0+z_0\) bằng
| \(-2\) | |
| \(13\) | |
| \(-5\) | |
| \(12\) |
Tính số đo góc giữa hai đường thẳng \(\Delta_1\colon3x-4y+5=0\) và \(\Delta_2\colon-2x+y+3=0\).
| \(63^\circ26'\) | |
| \(26^\circ63'\) | |
| \(153^\circ26'\) | |
| \(26^\circ34'\) |
Cho hình lăng trụ đều $ABC.A'B'C'$ có $AB=a$, $AA'=a\sqrt{3}$. Tính góc tạo bởi đường thẳng $AC'$ và mặt phẳng $(ABC)$.
| $60^\circ$ | |
| $45^\circ$ | |
| $30^\circ$ | |
| $75^\circ$ |
Cho hình chóp $S.ABC$ có $SA$ vuông góc với mặt phẳng $(ABC)$, $SA=2a$, tam giác $ABC$ vuông tại $B$, $AB=a\sqrt{3}$ và $BC=a$. Góc giữa đường thẳng $SC$ và mặt phẳng $(ABC)$ bằng
| $90^{\circ}$ | |
| $30^{\circ}$ | |
| $45^{\circ}$ | |
| $60^{\circ}$ |
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành tâm $I$ và $SA=SC$, $SB=SD$. Đường thẳng nào sau đây vuông góc với mặt phẳng $(ABCD)$?
| $SI$ | |
| $SA$ | |
| $SB$ | |
| $SC$ |
Cho hình chóp $S.ABC$ có cạnh bên $SA$ vuông góc với mặt đáy. Hình chiếu vuông góc của $SC$ trên mặt phẳng $(ABC)$ là đường thẳng
| $AC$ | |
| $BC$ | |
| $AB$ | |
| $SC$ |
Cho hình chóp $S.ABC$ có cạnh bên $SA$ vuông góc với mặt đáy. Hình chiếu vuông góc của $SB$ trên mặt phẳng $(ABC)$ là đường thẳng
| $AB$ | |
| $BC$ | |
| $SB$ | |
| $AC$ |
Cho hình chóp $S.ABC$ có cạnh bên $SA$ vuông góc với mặt đáy. Khẳng định nào sau đây không đúng?
| $SB\perp BC$ | |
| $SA\perp AB$ | |
| $SA\perp AC$ | |
| $SA\perp BC$ |
Biết rằng $b,\,c$ là hai đường thẳng cắt nhau và cùng nằm trong mặt phẳng $(\alpha)$. Nếu đường thẳng $a$ vuông góc với cả $b$ và $c$ thì
| $a\perp(\alpha)$ | |
| $a\parallel(\alpha)$ | |
| $a\subset(\alpha)$ | |
| $a,\,b,\,c$ đồng quy |
Biết rằng đường thẳng $a$ vuông góc với mặt phẳng $(\alpha)$ và đường thẳng $b$ nằm trên mặt phẳng $(\alpha)$. Kết luận nào sau đây là đúng?
| $a\perp b$ | |
| $a\parallel b$ | |
| $a,\,b$ chéo nhau | |
| $a,\,b$ cắt nhau |
