Cho hình lăng trụ đều $ABC.A'B'C'$ có $AB=a$, $AA'=a\sqrt{3}$. Tính góc tạo bởi đường thẳng $AC'$ và mặt phẳng $(ABC)$.
| $60^\circ$ | |
| $45^\circ$ | |
| $30^\circ$ | |
| $75^\circ$ |
Cho hình lăng trụ đứng $ABC.A'B'C'$ có đáy $ABC$ là tam giác vuông tại $B$, $AC=2$, $AB=\sqrt{3}$ và $AA'=1$ (tham khảo hình bên).
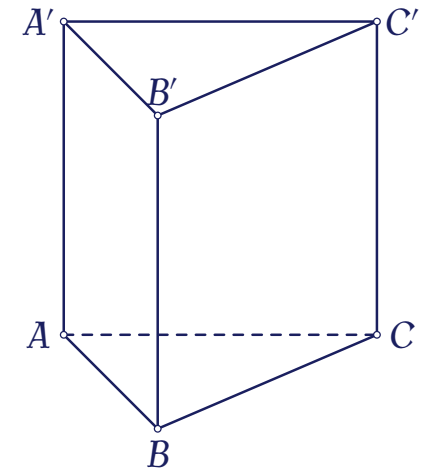
Góc giữa hai mặt phẳng $(ABC')$ và $(ABC)$ bằng
| $30^\circ$ | |
| $45^\circ$ | |
| $90^\circ$ | |
| $60^\circ$ |
Cho hình lăng trụ đứng $ABC.A'B'C'$ có tất cả các cạnh bằng nhau (tham khảo hình bên).
Góc giữa hai đường thẳng $AA'$ và $BC'$ bằng
| $30^\circ$ | |
| $90^\circ$ | |
| $45^\circ$ | |
| $60^\circ$ |
Cho hình lăng trụ có cạnh bên vuông góc với mặt đáy, khi đó các mặt bên của lăng trụ là hình gì?
| Hình chữ nhật | |
| Hình bình hành | |
| Hình thoi | |
| Hình vuông |
Cho hình lập phương $ABCD.A'B'C'D'$. Tính góc giữa 2 vectơ $\overrightarrow{AB},\,\overrightarrow{A'C'}$.
| $\big(\overrightarrow{AB},\overrightarrow{A'C'}\big)=45^\circ$ | |
| $\big(\overrightarrow{AB},\overrightarrow{A'C'}\big)=60^\circ$ | |
| $\big(\overrightarrow{AB},\overrightarrow{A'C'}\big)=30^\circ$ | |
| $\big(\overrightarrow{AB},\overrightarrow{A'C'}\big)=90^\circ$ |
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $a$, $SA\perp(ABC)$ và $SA=a$.
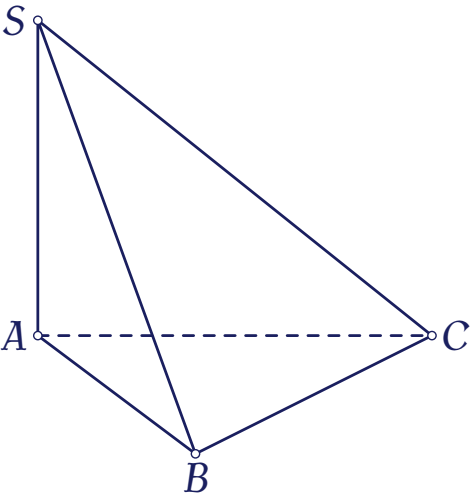
Góc giữa $SB$ và $AB$ bằng
| $60^{\circ}$ | |
| $90^{\circ}$ | |
| $135^{\circ}$ | |
| $45^{\circ}$ |
Trong không gian, cho hai đường thẳng $d$ và $d'$ có vectơ chỉ phương lần lượt là $\overrightarrow{u}$ và $\overrightarrow{v}$. Biết rằng $\cos\big(\overrightarrow{u},\overrightarrow{v}\big)=-\dfrac{1}{2}$, góc giữa hai đường thẳng $d$ và $d$ bằng bao nhiêu độ?
| $60^{\circ}$ | |
| $30^{\circ}$ | |
| $120^{\circ}$ | |
| $150^{\circ}$ |
Thể tích của khối lập phương cạnh \(2\) bằng
| \(6\) | |
| \(8\) | |
| \(4\) | |
| \(2\) |
Cho khối lập phương có cạnh bằng \(6\). Thể tích khối lập phương đã cho bằng
| \(216\) | |
| \(18\) | |
| \(36\) | |
| \(72\) |
Cho hình lăng trụ đều $ABC.A'B'C'$ có $AB=a$, $AA'=a\sqrt{3}$. Tính góc tạo bởi đường thẳng $AC'$ và mặt phẳng $(ABC)$.
| $60^\circ$ | |
| $45^\circ$ | |
| $30^\circ$ | |
| $75^\circ$ |
Cho khối lăng trụ đứng $ABC.A'B'C'$ có đáy $ABC$ là tam giác vuông cân tại $A$, $AB=2a$. Góc giữa đường thẳng $BC'$ và mặt phẳng $(ACC'A')$ bằng $30^\circ$. Thể tích của khối lăng trụ đã cho bằng
| $3a^3$ | |
| $a^3$ | |
| $12\sqrt{2}a^3$ | |
| $4\sqrt{2}a^3$ |
Cho khối hộp chữ nhật $ABCD.A'B'C'D'$ có đáy hình vuông. $BD=2a$, góc giữa hai mặt phẳng $\left(A'BD\right)$ và $(ABCD)$ bằng $30^\circ$. Thể tích của khối hộp chữ nhật đã cho bằng
| $6\sqrt{3}a^3$ | |
| $\dfrac{2\sqrt{3}}{9}a^3$ | |
| $2\sqrt{3}a^3$ | |
| $\dfrac{2\sqrt{3}}{3}a^3$ |
Cho hình hộp $ABCD.A'B'C'D'$ có tất cả các cạnh bằng nhau (tham khảo hình bên).
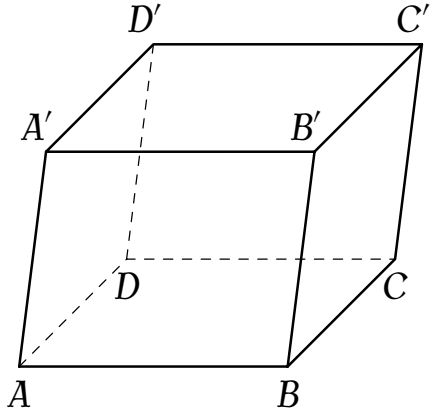
Góc giữa hai đường thẳng $A'C'$ và $BD$ bằng
| $90^{\circ}$ | |
| $30^{\circ}$ | |
| $45^{\circ}$ | |
| $60^{\circ}$ |
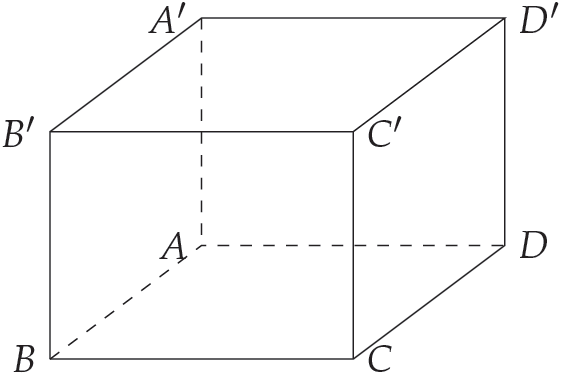
Cho hình lăng trụ đứng \(ABCD.A'B'C'D'\) có đáy là hình thoi cạnh \(a\), \(BD=a\sqrt{3}\), \(AA'=4a\) (minh họa như hình trên). Thể tích của khối lăng trụ đã cho bằng
| \(2\sqrt{3}a^3\) | |
| \(4\sqrt{3}a^3\) | |
| \(\dfrac{2\sqrt{3}a^3}{3}\) | |
| \(\dfrac{4\sqrt{3}a^3}{3}\) |
Hình lăng trụ $ABC.A'B'C'$ có đáy $ABC$ là tam giác vuông tại $A$, $AB=a$, $AC=2a$. Hình chiếu vuông góc của $A'$ lên mặt phẳng $(ABC)$ là điểm $I$ thuộc cạnh $BC$. Khoảng cách từ $A$ tới mặt phẳng $(A'BC)$ bằng
| $\dfrac{2}{5}a$ | |
| $\dfrac{\sqrt{3}}{2}a$ | |
| $\dfrac{2a\sqrt{5}}{5}$ | |
| $\dfrac{a\sqrt{5}}{5}$ |
Cho hình chóp $S.ABC$ có $SA$ vuông góc với mặt phẳng $(ABC)$, $SA=2a$, tam giác $ABC$ vuông tại $B$, $AB=a\sqrt{3}$ và $BC=a$. Góc giữa đường thẳng $SC$ và mặt phẳng $(ABC)$ bằng
| $90^{\circ}$ | |
| $30^{\circ}$ | |
| $45^{\circ}$ | |
| $60^{\circ}$ |
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $a$, cạnh bên $SA=a$ và vuông góc với mặt đáy. Góc giữa đường thẳng $SC$ và mặt phẳng $(ABC)$ có số đo
| $45^\circ$ | |
| $90^\circ$ | |
| $30^\circ$ | |
| $60^\circ$ |
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $a$, cạnh bên $SA=a\sqrt{3}$ và vuông góc với mặt đáy. Góc giữa đường thẳng $SB$ và mặt phẳng $(ABC)$ có số đo
| $60^\circ$ | |
| $90^\circ$ | |
| $30^\circ$ | |
| $45^\circ$ |
Cho hình chóp $S.ABC$ có $SA\perp AB$ và $SA\perp BC$. Khẳng định nào sau đây không đúng?
| $AB\perp BC$ | |
| $SA\perp AC$ | |
| $SA\perp(ABC)$ | |
| $\big(SA,(ABC)\big)=90^\circ$ |
Cho hình chóp $S.ABC$ có cạnh bên $SA$ vuông góc với mặt đáy. Góc giữa đường thẳng $SC$ và mặt phẳng $(ABC)$ là góc
| $\widehat{SCA}$ | |
| $\widehat{SCB}$ | |
| $\widehat{SAC}$ | |
| $\widehat{ASC}$ |
