Cho khối nón đỉnh $S$ có bán kính đáy bằng $2\sqrt{3}a$. Gọi $A$ và $B$ là hai điểm thuộc đường tròn đáy sao cho $AB=4a$. Biết khoảng cách từ tâm của đáy đến mặt phẳng $(SAB)$ bằng $2a$, thể tích của khối nón đã cho bằng
 | $\dfrac{8\sqrt{2}}{3}\pi a^3$ |
 | $4\sqrt{6}\pi a^3$ |
 | $\dfrac{16\sqrt{3}}{3}\pi a^3$ |
 | $8\sqrt{2}\pi a^3$ |
Cho hình nón đỉnh $S$, đường cao $SO$, $A$ và $B$ là hai điểm thuộc đường tròn đáy sao cho khoảng cách từ $O$ đến $(SAB)$ bằng $\dfrac{a\sqrt{3}}{3}$ và $\widehat{SAO}=30^{\circ}$, $\widehat{SAB}=60^{\circ}$. Độ dài đường sinh của hình nón theo $a$ bằng
| $a\sqrt{2}$ |
| $a\sqrt{3}$ |
| $2a\sqrt{3}$ |
| $a\sqrt{5}$ |
Cho hình nón $S$ có chiều cao bằng $3a$. Mặt phẳng $\left(P\right)$ đi qua $S$ cắt đường tròn đáy tại hai điểm $A$ và $B$ sao cho $AB=6\sqrt{3}a$. Biết khoảng cách từ tâm của đường tròn đáy đến $\left(P\right)$ bằng $\dfrac{3a\sqrt{2}}{2}$. Thể tích $V$ của khối nón bị giới hạn bởi hình nón đã cho bằng
| $V=54\pi a^3$ |
| $V=108\pi a^3$ |
| $V=36\pi a^3$ |
| $V=18\pi a^3$ |
Xét khối nón $(\mathscr{N})$ có đỉnh và đường tròn đáy cùng nằm trên một mặt cầu bán kính bằng 2. Khi $(\mathscr{N})$ có độ dài đường sinh bằng $2\sqrt{3}$, thể tích của nó bằng
| $2\sqrt{3}\pi$ |
| $3\pi$ |
| $6\sqrt{3}\pi$ |
| $\pi$ |
Một bình đựng nước dạng hình nón (không có nắp đậy), đựng đầy nước. Biết rằng chiều cao của bình gấp $3$ lần bán kính đáy của nó. Người ta thả vào bình đó một khối trụ và đo được thể tích nước tràn ra ngoài là $\dfrac{16\pi}{9}\text{dm}^3$. Biết rằng một mặt của khối trụ nằm trên mặt đáy của hình nón và khối trụ có chiều cao bằng đường kính đáy của hình nón (hình vẽ).
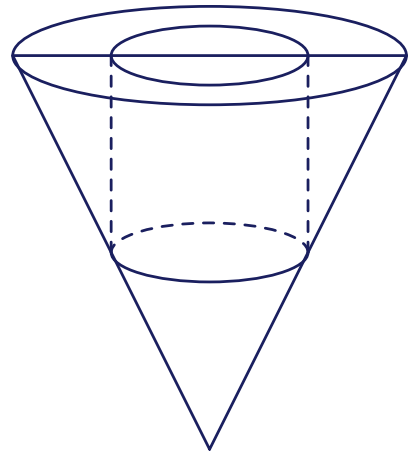
Tính bán kính đáy $R$ của bình nước.
| $R=4$dm |
| $R=2$dm |
| $R=3$dm |
| $R=5$dm |
Trên bàn có một cốc nước hình trụ chứa đầy nước, có chiều cao bằng $3$ lần đường kính của đáy; một viên bi và một khối nón đều bằng thủy tinh. Biết viên bi là một khối cầu có đường kính bằng đường kính của cốc nước. Người ta từ từ thả vào cốc nước viên bi và khối nón sao cho đỉnh khối nón nằm trên mặt cầu (như hình vẽ) thì thấy nước trong cốc tràn ra ngoài.
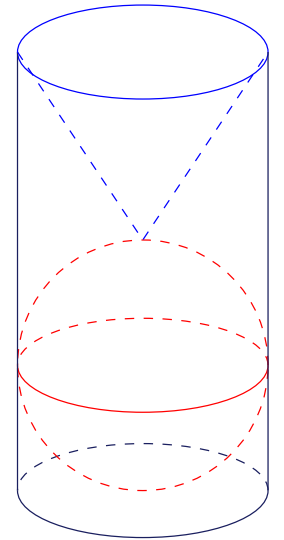
Tính tỉ số thể tích của lượng nước còn lại trong cốc và lượng nước ban đầu (bỏ qua bề dày của lớp vỏ thủy tinh).
| $\dfrac{1}{2}$ |
| $\dfrac{2}{3}$ |
| $\dfrac{4}{9}$ |
| $\dfrac{5}{9}$ |
Trền bàn có một cốc nước hình trụ chứa đầy nước, có chiều cao bằng 3 lần đường kính của đáy; một viên bi và một khối nón đều bằng thủy tinh. Biết viên bi là một khối cầu có đường kính bằng đường kính của cốc nước. Người ta từ từ thả vào cốc nước viên bi và khối nón sao cho đỉnh khối nón nằm trên mặt cầu (như hình vẽ) thì thấy nước trong cốc tràn ra ngoài.
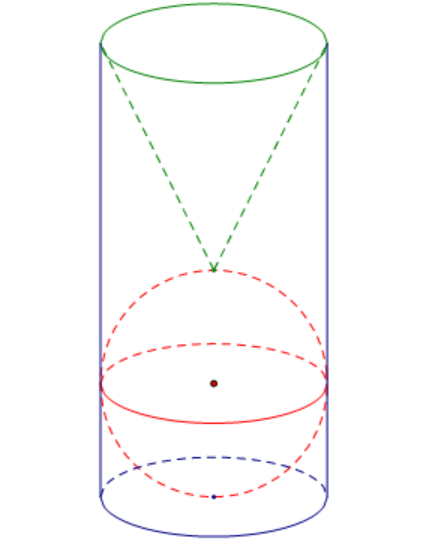
Tính tỉ số thể tích của lượng nước còn lại trong cốc và lượng nước ban đầu (bỏ qua bề dày của lớp vỏ thủy tinh).
Trong không gian \(Oxyz\), cho mặt cầu \((S)\colon(x-1)^2+(y-1)^2+(z-1)^2=25\) có tâm \(I\) và mặt phẳng \((P)\colon x+2y+2z+7=0\). Thể tích của khối nón có đỉnh \(I\) và đáy là giao tuyến của mặt cầu \((S)\) và mặt phẳng \((P)\) bằng
| \(12\pi\) |
| \(48\pi\) |
| \(36\pi\) |
| \(24\pi\) |
Cho khối hộp $ABCD.A'B'C'D'$ có thể tích bằng $6a^3$ và diện tích tam giác $A'BD$ bằng $a^2$. Khoảng cách từ điểm $A$ đến mặt phẳng $(B'CD')$ bằng
| $6a$ |
| $2a$ |
| $3a$ |
| $a$ |
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật và $AD=a$, $AB=2a$. Biết tam giác $SAB$ là tam giác đều và mặt phẳng $(SAB)$ vuông góc với mặt phẳng $(ABCD)$. Tính khoảng cách từ điểm $A$ đến mặt phẳng $(SBD)$.
| $\dfrac{a\sqrt{3}}{4}$ |
| $\dfrac{a\sqrt{3}}{2}$ |
| $a\sqrt{3}$ |
| $\dfrac{a\sqrt{3}}{3}$ |
Trong không gian \(Oxyz\), cho tứ diện \(ABCD\) với \(A(1;2;1)\), \(B(2;1;3)\), \(C(3;2;2)\), \(D(1;1;1)\). Độ dài chiều cao \(DH\) của tứ diện bằng
| \(\dfrac{\sqrt{14}}{14}\) |
| \(\dfrac{3\sqrt{14}}{14}\) |
| \(\dfrac{3\sqrt{14}}{7}\) |
| \(\dfrac{4\sqrt{14}}{7}\) |
Khối nón có chiều cao $h=3$cm và bán kính đáy $r=2$cm thì có thể tích bằng bao nhiêu?
| $4\pi\text{ cm}^3$ |
| $16\pi\text{ cm}^3$ |
| $\dfrac{4}{3}\pi\text{ cm}^3$ |
| $4\pi\text{ cm}^2$ |
Cho khối nón có diện tích đáy $B=a^2$ và chiều cao $h=3a$. Thể tích của khối nón bằng
| $a^3$ |
| $3a^3$ |
| $2a^3$ |
| $4a^3$ |
Một vật rắn gồm một nửa hình cầu, một hình trụ và một hình nón có hình dạng và kích thước như hình bên dưới.
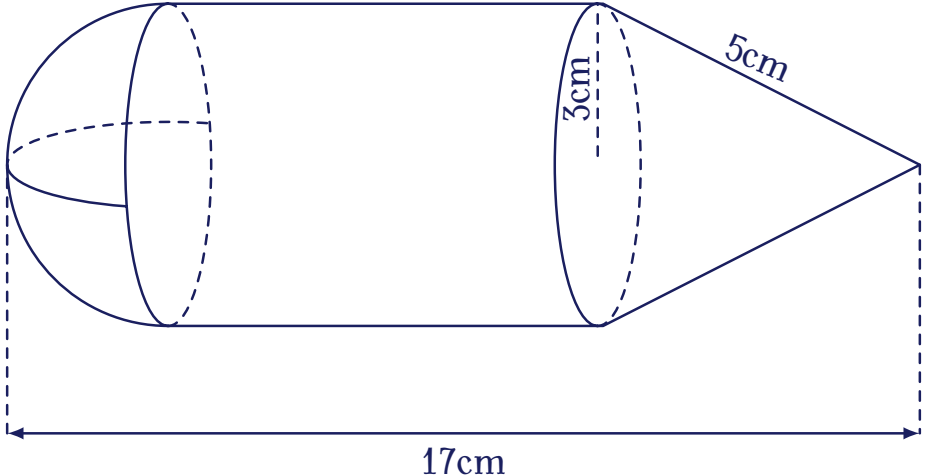
Thể tích của vật rắn đã cho bằng
| $120\pi\text{ cm}^3$ |
| $144\pi\text{ cm}^3$ |
| $126\pi\text{ cm}^3$ |
| $111\pi\text{ cm}^3$ |
Cho hình chóp tứ giác đều $S.ABCD$ có cạnh đáy là $2a$ và chiều cao là $3a$. Thể tích của khối nón có đỉnh $S$ và đáy là đường tròn nội tiếp tứ giác $ABCD$ bằng
| $4\pi a^3$ |
| $\pi a^3$ |
| $3\pi a^3$ |
| $2\pi a^3$ |
Thể tích của khối nón có chiều cao $h$ và bán kính $r$ là
| $\dfrac{4}{3}\pi r^2h$ |
| $2\pi r^2h$ |
| $\pi r^2h$ |
| $\dfrac{1}{3}\pi r^2h$ |
Cho khối nón có diện tích đáy $B=a^2$ và chiều cao $h=3a$. Thể tích của khối nón bằng
| $a^3$ |
| $3a^3$ |
| $2a^3$ |
| $4a^3$ |
Cho mặt cầu $\mathscr{S}(O,r)$, biết khoảng cách từ $O$ tới mặt phẳng $(P)$ bằng $\dfrac{r}{3}$. Mặt phẳng $(P)$ cắt mặt cầu theo một đường tròn có bán kính bằng
| $\dfrac{2r\sqrt{2}}{3}$ |
| $r\sqrt{3}$ |
| $\dfrac{2r}{3}$ |
| $\dfrac{r\sqrt{3}}{3}$ |
Cho hình nón có góc ở đỉnh bằng $120^\circ$ và chiều cao bằng $4$. Gọi $(S)$ là mặt cầu đi qua đỉnh và chứa đường tròn đáy của hình nón đã cho. Diện tích của $(S)$ bằng
| $64\pi$ |
| $256\pi$ |
| $192\pi$ |
| $96\pi$ |
Thiết diện qua trục của một hình nón tròn xoay là tam giác đều có diện tích bằng $a^2\sqrt{3}$. Tính thể tích $V$ của khối nón đã cho.
| $V=\dfrac{\pi a^3\sqrt{3}}{3}$ |
| $V=\dfrac{\pi a^3\sqrt{3}}{2}$ |
| $V=\dfrac{\pi a^3\sqrt{3}}{6}$ |
| $V=\dfrac{\pi a^3\sqrt{6}}{6}$ |