Trong không gian, cho tứ diện $ABCD$ có trọng tâm $S$. Gọi $G$ là trọng tâm tam giác $BCD$, $M$ và $N$ lần lượt là trung điểm của $AB$, $CD$. Mệnh đề nào sau đây là sai?
| $S$ là trung điểm đoạn $MN$ | |
| $\overrightarrow{SA}+\overrightarrow{SB}+\overrightarrow{SC}+\overrightarrow{SD}=\overrightarrow{0}$ | |
| $S$ nằm trên đoạn $AG$ sao cho $SA=3SG$ | |
| $\overrightarrow{SA}+\overrightarrow{SB}+\overrightarrow{SC}+\overrightarrow{SD}=\overrightarrow{0}$ |
Trong không gian, điểm $S$ là trọng tâm của tứ diện $ABCD$ nếu
| $\overrightarrow{SA}+\overrightarrow{SB}+\overrightarrow{SC}+\overrightarrow{SD}=\overrightarrow{0}$ | |
| $\overrightarrow{SA}+\overrightarrow{SB}=\overrightarrow{SC}+\overrightarrow{SD}$ | |
| $\overrightarrow{SA}+\overrightarrow{SB}+\overrightarrow{SC}=3\overrightarrow{SD}$ | |
| $\overrightarrow{SA}+\overrightarrow{SB}+\overrightarrow{SC}=\overrightarrow{A0}$ |
Cho tứ diện $ABCD$ có $G$ là trọng tâm tam giác $BCD$. Mệnh đề nào sau đây không đúng?
| $\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}=3\overrightarrow{AG}$ | |
| $\overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{GD}=\overrightarrow{0}$ | |
| $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}$ | |
| $\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}-3\overrightarrow{AG}=\overrightarrow{0}$ |
Trong không gian, điểm $S$ là trọng tâm của tam giác $ABC$ nếu
| $\overrightarrow{SA}+\overrightarrow{SB}+\overrightarrow{SC}=\overrightarrow{0}$ | |
| $\overrightarrow{SA}+\overrightarrow{SB}=\overrightarrow{SC}$ | |
| $\overrightarrow{SA}+\overrightarrow{SB}=\overrightarrow{0}$ | |
| $\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AS}$ |
Cho hình chóp $S.ABC$. Gọi $M,\,N,\,P$ lần lượt là trung điểm của $SA,\,SB,\,SC$. Chọn khẳng định đúng.
| $(MNP)\parallel(ABC)$ | |
| $(MNP)\parallel(SAC)$ | |
| $(SMN)\parallel(ABC)$ | |
| $(MNP)\parallel(SBC)$ |
Cho hình chóp $S.ABC$ có tam giác $ABC$ vuông cân tại $A$, $AB=AC=a$ và $SA=SB=SC=a$. Tính $\overrightarrow{AB}\cdot\overrightarrow{SC}$.
| $\overrightarrow{AB}\cdot\overrightarrow{SC}=-\dfrac{a^2}{2}$ | |
| $\overrightarrow{AB}\cdot\overrightarrow{SC}=\dfrac{a^2}{2}$ | |
| $\overrightarrow{AB}\cdot\overrightarrow{SC}=\dfrac{a^2\sqrt{3}}{2}$ | |
| $\overrightarrow{AB}\cdot\overrightarrow{SC}=-\dfrac{a^2\sqrt{3}}{2}$ |
Cho hình hộp $ABCD.A'B'C'D'$ (tham khảo hình vẽ).
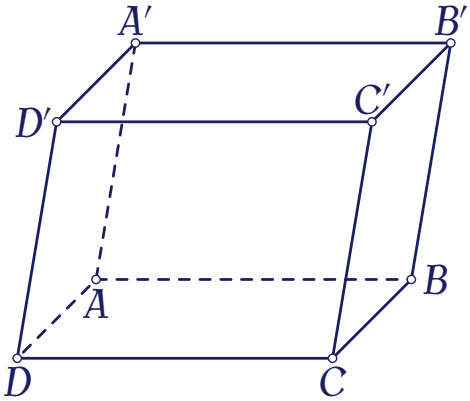
Khẳng định nào sau đây là đúng?
| $\overrightarrow{BA}+\overrightarrow{BC}+\overrightarrow{BB'}=\overrightarrow{BA'}$ | |
| $\overrightarrow{BA}+\overrightarrow{BC}+\overrightarrow{BB'}=\overrightarrow{B'D}$ | |
| $\overrightarrow{BA}+\overrightarrow{BC}+\overrightarrow{BB'}=\overrightarrow{BD'}$ | |
| $\overrightarrow{BA}+\overrightarrow{BC}+\overrightarrow{BB'}=\overrightarrow{BC'}$ |
Cho tứ diện $ABCD$. Gọi $N,\,K$ lần lượt là trung điểm các cạnh $BC$ và $CD$, $M$ là điểm trên cạnh $AB$ sao cho $MB=2MA$. Thiết diện của tứ diện $ABCD$ cắt bởi mặt phẳng $(MNK)$ là
| Hình bình hành | |
| Hình thang | |
| Hình chữ nhật | |
| Hình thoi |
Cho tứ diện $ABCD$. Gọi $M,\,N,\,K$ lần lượt là trung điểm các cạnh $AB$, $BC$, $CD$. Thiết diện của tứ diện $ABCD$ cắt bởi mặt phẳng $(MNK)$ là
| Hình bình hành | |
| Hình thang | |
| Hình chữ nhật | |
| Hình thoi |
Cho $4$ điểm không đồng phẳng $A,\,B,\,C,\,D$. Gọi $I,\,K$ lần lượt là trung điểm của $AD$ và $BC$. Giao tuyến của $(IBC)$ và $(KAD)$ là
| $IK$ | |
| $BC$ | |
| $AK$ | |
| $DK$ |
Cho tam giác \(ABC\), trung tuyến \(AM\). Đẳng thức nào sau đây không đúng?
| \(\overrightarrow{MA}+\overrightarrow{MB}=\overrightarrow{0}\) | |
| \(\overrightarrow{MB}+\overrightarrow{MC}=\overrightarrow{0}\) | |
| \(\overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AM}\) | |
| \(\overrightarrow{MB}-\overrightarrow{MC}=\overrightarrow{CB}\) |
Cho tam giác \(ABC\) có trọng tâm \(G\), \(M\) là trung điểm cạnh \(BC\). Mệnh đề nào sau đây sai?
| \(\overrightarrow{MB}+\overrightarrow{MC}=\vec{0}\) | |
| \(\overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AM}\) | |
| \(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\vec{0}\) | |
| \(\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=-3\overrightarrow{MG}\) |
Gọi \(M\) là trung điểm của đoạn thẳng \(AB\). Khẳng định nào sau đây là sai?
| \(\overrightarrow{AB}=2\overrightarrow{MB}\) | |
| \(\overrightarrow{MA}+\overrightarrow{MB}=\vec{0}\) | |
| \(\overrightarrow{MA}=-\dfrac{1}{2}\overrightarrow{AB}\) | |
| \(\overrightarrow{MA}=\overrightarrow{MB}\) |
Cho hình bình hành \(ABCD\), tâm \(M\). Mệnh đề nào sau đây sai?
| \(\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}\) | |
| \(\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}\) | |
| \(\overrightarrow{BA}+\overrightarrow{BC}=2\overrightarrow{BM}\) | |
| \(\overrightarrow{MA}+\overrightarrow{MB}=\overrightarrow{MC}+\overrightarrow{MD}\) |
Cho tam giác \(ABC\) có \(G\) là trọng tâm và \(I\) là trung điểm cạnh \(BC\). Đẳng thức nào sau đây đúng?
| \(\overrightarrow{GA}=2\overrightarrow{GI}\) | |
| \(\overrightarrow{IG}=-\dfrac{1}{3}\overrightarrow{IA}\) | |
| \(\overrightarrow{GB}+\overrightarrow{GC}=2\overrightarrow{GI}\) | |
| \(\overrightarrow{GB}+\overrightarrow{GC}=2\overrightarrow{GA}\) |
Cho tam giác \(ABC\) có \(M\) là trung điểm của \(BC\), \(I\) là trung điểm của \(AM\). Khẳng định nào sau đây đúng?
| \(\overrightarrow{IB}+2\overrightarrow{IC}+\overrightarrow{IA}=\vec{0}\) | |
| \(\overrightarrow{IB}+\overrightarrow{IC}+2\overrightarrow{IA}=\vec{0}\) | |
| \(2\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{IA}=\vec{0}\) | |
| \(\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{IA}=\vec{0}\) |
Cho tam giác \(ABC\) có $M$ là điểm thỏa mãn \(\overrightarrow{MB}+\overrightarrow{MC}=\overrightarrow{AB}\). Xác định vị trí điểm \(M\).
| \(M\) là trung điểm cạnh \(AC\) | |
| \(M\) là trung điểm cạnh \(AB\) | |
| \(M\) là trung điểm cạnh \(BC\) | |
| \(M\) là điểm thứ tư của hình bình hành \(ABCM\) |
Cho tam giác \(ABC\) có \(D,\,E,\,F\) lần lượt là trung điểm các cạnh \(BC,\,CA,\,AB\). Hệ thức nào sau đây đúng?
| \(\overrightarrow{AD}+\overrightarrow{BE}+\overrightarrow{CF}=\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{BC}\) | |
| \(\overrightarrow{AD}+\overrightarrow{BE}+\overrightarrow{CF}=\overrightarrow{CA}+\overrightarrow{BC}+\overrightarrow{AC}\) | |
| \(\overrightarrow{AD}+\overrightarrow{BE}+\overrightarrow{CF}=\overrightarrow{AE}+\overrightarrow{BF}+\overrightarrow{CD}\) | |
| \(\overrightarrow{AD}+\overrightarrow{BE}+\overrightarrow{CF}=\overrightarrow{BA}+\overrightarrow{BC}+\overrightarrow{AC}\) |
Cho hình bình hành \(ABCD\) tâm \(O\). Hãy tìm đẳng thức đúng.
| \(\overrightarrow{OA}+\overrightarrow{OB}=\overrightarrow{AB}\) | |
| \(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}-\overrightarrow{OD}=\vec{0}\) | |
| \(\overrightarrow{OA}+\overrightarrow{OB}=\overrightarrow{OC}-\overrightarrow{OD}\) | |
| \(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}=\vec{0}\) |
Cho tam giác \(ABC\) có \(AB=AC\) và đường cao \(AH\). Đẳng thức nào sau đây đúng?
| \(\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AH}\) | |
| \(\overrightarrow{HA}+\overrightarrow{HB}+\overrightarrow{HC}=\vec{0}\) | |
| \(\overrightarrow{HB}+\overrightarrow{HC}=\vec{0}\) | |
| \(\overrightarrow{AB}=\overrightarrow{AC}\) |
