Cho hàm số bậc hai $y=f(x)$ có đồ thị $(P)$ và đường thẳng $d$ cắt $(P)$ tại hai điểm như trong hình vẽ bên.
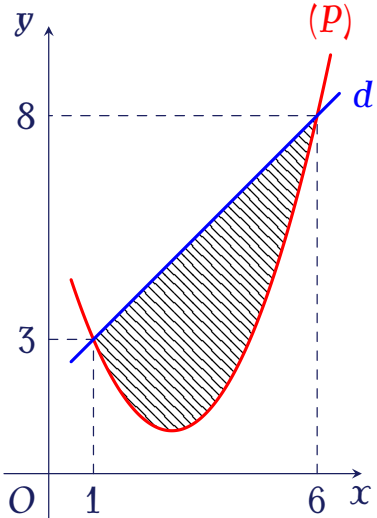
Biết rằng hình phẳng giới hạn bởi $(P)$ và $d$ có diện tích $S=\dfrac{125}{9}$. Tích phân $\displaystyle\displaystyle\int\limits_1^6(2x-5)f'(x)\mathrm{~d}x$ bằng
| $\dfrac{830}{9}$ | |
| $\dfrac{178}{9}$ | |
| $\dfrac{340}{9}$ | |
| $\dfrac{925}{18}$ |
Cho hàm số $f(x)$ có đạo hàm $f'(x)$ liên tục trên $\mathbb{R}$ và thỏa mãn $\displaystyle\displaystyle\int\limits_{0}^{1}(3x+1)f'(x)\mathrm{\,d}x=2022$ và $4f(1)-f(0)=2028$. Giá trị của $I=\displaystyle\displaystyle\int\limits_{0}^{\tfrac{1}{4}}f(4x)\mathrm{\,d}x$ là
| $2$ | |
| $\dfrac{2022}{3}$ | |
| $\dfrac{1}{2}$ | |
| $\dfrac{1}{4}$ |
Cho hàm số $f(x)$ thỏa mãn $f(x)=x\mathrm{e}^x+\displaystyle\int\limits_{0}^{2}\left(f(x)+f'(x)-\mathrm{e}^x-1\right)\mathrm{\,d}x$. Tính tích phân $\displaystyle\int\limits_{0}^{1}f(x)\mathrm{\,d}x$.
| $2\mathrm{e}^2-1$ | |
| $-2\mathrm{e}^2-1$ | |
| $-2\mathrm{e}^2+1$ | |
| $2\mathrm{e}^2+1$ |
Cho hàm số $y=f(x)$ có đạo hàm liên tục trên $\mathbb{R}$ và thỏa mãn $2f(x)+f'(x)=2x+1$, $\forall x\in\mathbb{R}$ và $f(0)=1$. Giá trị của $\displaystyle\int\limits_{0}^{1}f(x)\mathrm{\,d}x$ bằng
| $1-\dfrac{1}{2\mathrm{e}^2}$ | |
| $1+\dfrac{1}{2\mathrm{e}^2}$ | |
| $\dfrac{1}{2\mathrm{e}^2}$ | |
| $-\dfrac{1}{2\mathrm{e}^2}$ |
Cho hàm số $y=f(x)$ có đạo hàm liên tục trên $\mathbb{R}$ và thỏa mãn $f(x)+xf'(x)=4x^3+4x+2$, $\forall x\in\mathbb{R}$. Diện tích hình phẳng giới hạn bởi các đường $y=f(x)$ và $y=f'(x)$ bằng
| $\dfrac{5}{2}$ | |
| $\dfrac{4}{3}$ | |
| $\dfrac{1}{2}$ | |
| $\dfrac{1}{4}$ |
Cho hàm số $f\left(x\right)$ thỏa mãn $f\left(2\right)=25$ và $f'\left(x\right)=4x\sqrt{f\left(x\right)}$ với mọi $x\in\mathbb{R}$. Khi đó $\displaystyle\displaystyle\int\limits_2^3f\left(x\right)\mathrm{\,d}x$ bằng
| $\dfrac{1073}{15}$ | |
| $\dfrac{458}{15}$ | |
| $\dfrac{838}{15}$ | |
| $\dfrac{1016}{15}$ |
Cho hàm số $f(x)$ có đạo hàm liên tục trên $\mathbb{R}$, thỏa mãn $f(x)+2f(2-x)=x^2-6x+4$. Tích phân $\displaystyle\displaystyle\int\limits_{-1}^3x f^{\prime}(x)\mathrm{d}x$ bằng
| $20$ | |
| $\dfrac{149}{3}$ | |
| $\dfrac{167}{3}$ | |
| $\dfrac{176}{9}$ |
Cho hàm số $f(x)$ có đạo hàm liên tục trên $\mathbb{R}$ thỏa mãn $f(x)=x^2-3x+2\displaystyle\int\limits_{0}^{1}f(x)f'(x)\mathrm{\,d}x$. Khi đó $\displaystyle\int\limits_{0}^{2}f(x)\mathrm{\,d}x$ bằng
| $\dfrac{10}{3}$ | |
| $-\dfrac{10}{3}$ | |
| $\dfrac{26}{15}$ | |
| $-\dfrac{26}{15}$ |
Xét hàm số $f(x)=\mathrm{e}^x+\displaystyle\int\limits_{0}^{1}xf(x)\mathrm{\,d}x$. Giá trị $f\left(\ln5620\right)$ bằng
| $5622$ | |
| $5620$ | |
| $5618$ | |
| $5621$ |
Cho hàm số $f(x)$ liên tục trên đoạn $[1;2]$. Biết $f(2)=a$ và $\displaystyle\displaystyle\int\limits_{1}^{2}(x-1)f'(x)\mathrm{\,d}x=b$. Tích phân $\displaystyle\displaystyle\int\limits_{1}^{2}f(x)\mathrm{\,d}x$ có giá trị bằng
| $a-b$ | |
| $b-a$ | |
| $a+b$ | |
| $-a-b$ |
Cho $F(x)$ là một nguyên hàm của hàm số $f(x)$ trên đoạn $[1;3]$, $F(1)=3$, $F(3)=5$ và $\displaystyle\displaystyle\int\limits_1^3\left(x^4-8x\right)f(x)\mathrm{\,d}x=12$. Tính $I=\displaystyle\displaystyle\int\limits_1^3\left(x^3-2\right)F(x)\mathrm{\,d}x$.
| $I=\dfrac{147}{2}$ | |
| $I=\dfrac{147}{3}$ | |
| $I=-\dfrac{147}{2}$ | |
| $I=147$ |
Cho hàm số $y=f(x)$ liên tục, thỏa mãn $f(x)=x\left(1+\dfrac{1}{\sqrt{x}}-f'(x)\right)$, $\forall x\in(0;+\infty)$ và $f(4)=\dfrac{4}{3}$. Giá trị của $\displaystyle\displaystyle\int\limits_{1}^{4}\left(x^2-1\right)f'(x)\mathrm{\,d}x$ bằng
| $\dfrac{457}{15}$ | |
| $\dfrac{457}{30}$ | |
| $-\dfrac{263}{30}$ | |
| $-\dfrac{263}{15}$ |
Cho hàm số $y=f(x)$ liên tục trên khoảng $(0;+\infty)$. Biết $f(1)=1$ và $f(x)=xf'(x)+\ln x$, $\forall x\in(0;+\infty)$. Giá trị của $f(\mathrm{e})$ bằng
| $\mathrm{e}$ | |
| $\dfrac{1}{\mathrm{e}}$ | |
| $1$ | |
| $2$ |
Cho hàm số $f(x)$ thỏa mãn $\displaystyle\displaystyle\int\limits_{0}^{1}(x+1)f'(x)\mathrm{\,d}x=10$ và $2f(1)-f(0)=2$. Tính $I=\displaystyle\displaystyle\int\limits_{0}^{1}f(x)\mathrm{\,d}x$.
| $I=-12$ | |
| $I=8$ | |
| $I=12$ | |
| $I=-8$ |
Cho hàm số \(y=f(x)\) có đạo hàm liên tục trên \(\mathbb{R}\) và thỏa mãn \(f(2)=16\), \(\displaystyle\int\limits_{0}^{2}f(x)\mathrm{\,d}x=4\). Tính \(I=\displaystyle\int\limits_{0}^{1}xf'(2x)\mathrm{\,d}x\).
| \(I=13\) | |
| \(I=20\) | |
| \(I=12\) | |
| \(I=7\) |
Cho hàm số \(y=f(x)\) liên tục, nhận giá trị dương trên \((0;+\infty)\) và thỏa mãn \(f(1)=1\), \(f(x)=f'(x)\sqrt{3x+1}\), với mọi \(x>0\). Mệnh đề nào sau đây đúng?
| \(4< f(5)<5\) | |
| \(3< f(5)<4\) | |
| \(1< f(5)<2\) | |
| \(2< f(5)<3\) |
Cho hàm số \(y=f(x)\) có đạo hàm \(f'(x)\) liên tục trên \([0;2]\) và \(f(2)=3\), \(\displaystyle\int\limits_{0}^{2}f(x)\mathrm{\,d}x=3\). Tính \(\displaystyle\int\limits_{0}^{2}x\cdot f'(x)\mathrm{\,d}x\).
| \(6\) | |
| \(3\) | |
| \(0\) | |
| \(-3\) |
Biết $F(x)=-\dfrac{1}{x^2}$ là một nguyên hàm của hàm số $y=\dfrac{f(x)}{x}$. Tính $\displaystyle\displaystyle\int f'(x)\ln{x}\mathrm{\,d}x$.
| $\displaystyle\displaystyle\int\limits f'(x)\ln{x}\mathrm{\,d}x=-\dfrac{2\ln{x}}{x^2}+\dfrac{1}{x^2}+C$ | |
| $\displaystyle\displaystyle\int\limits f'(x)\ln{x}\mathrm{\,d}x=\dfrac{2\ln{x}}{x^2}+\dfrac{1}{x^2}+C$ | |
| $\displaystyle\displaystyle\int\limits f'(x)\ln{x}\mathrm{\,d}x=\dfrac{2\ln{x}}{x^2}-\dfrac{1}{x^2}+C$ | |
| $\displaystyle\displaystyle\int\limits f'(x)\ln{x}\mathrm{\,d}x=-\dfrac{2\ln{x}}{x^2}-\dfrac{1}{x^2}+C$ |
Cho hàm số $y=f(x)$ có đạo hàm liên tục trên $\mathbb{R}$ và thỏa mãn $f(x)+x f'(x)=4x^3-6x^2$, $\forall x\in\mathbb{R}$. Diện tích hình phẳng giới hạn bởi các đường $y=f(x)$ và $y=f'(x)$ bằng
| $\dfrac{7}{12}$ | |
| $\dfrac{45}{4}$ | |
| $\dfrac{1}{2}$ | |
| $\dfrac{71}{6}$ |
Biết $F(x)$ và $G(x)$ là hai nguyên hàm của hàm số $f(x)$ trên $\mathbb{R}$ và $\displaystyle\displaystyle\int\limits_{0}^{3}f(x)\mathrm{\,d}x=F(3)-G(0)+a$ ($a>0$). Gọi $S$ là diện tích hình phẳng giới hạn bởi các đường $y=F(x)$, $y=G(x)$, $x=0$ và $x=3$. Khi $S=15$ thì $a$ bằng
| $15$ | |
| $12$ | |
| $18$ | |
| $5$ |
