Cho hàm số bậc hai $y=f(x)$ có đồ thị $(P)$ và đường thẳng $d$ cắt $(P)$ tại hai điểm như trong hình vẽ bên.
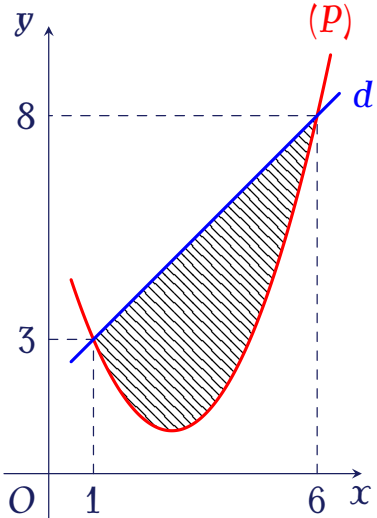
Biết rằng hình phẳng giới hạn bởi $(P)$ và $d$ có diện tích $S=\dfrac{125}{9}$. Tích phân $\displaystyle\displaystyle\int\limits_1^6(2x-5)f'(x)\mathrm{~d}x$ bằng
| $\dfrac{830}{9}$ | |
| $\dfrac{178}{9}$ | |
| $\dfrac{340}{9}$ | |
| $\dfrac{925}{18}$ |
Gọi $(H)$ là hình phẳng giới hạn bởi parabol $(P)\colon y=2x-x^2$ và trục hoành. Đường thẳng $y=mx$ chia hình $(H)$ thành hai phần có diện tích bằng nhau. Tính giá trị $m$.
| $2-\sqrt[3]{4}$ | |
| $2-\sqrt{3}$ | |
| $2-\sqrt{4}$ | |
| $2-\sqrt[3]{5}$ |
Cho hàm số $y=f(x)$ có đạo hàm liên tục trên $\mathbb{R}$ và thỏa mãn $f(x)+xf'(x)=4x^3+4x+2$, $\forall x\in\mathbb{R}$. Diện tích hình phẳng giới hạn bởi các đường $y=f(x)$ và $y=f'(x)$ bằng
| $\dfrac{5}{2}$ | |
| $\dfrac{4}{3}$ | |
| $\dfrac{1}{2}$ | |
| $\dfrac{1}{4}$ |
Cho hàm số $f(x)=x^3+ax^2+bx+c$ với $a,\,b,\,c$ là các số thực. Biết hàm số $g(x)=f(x)+f'(x)+f''(x)$ có hai giá trị cực trị là $-3$ và $6$. Diện tích hình phẳng giới hạn bởi các đường $y=\dfrac{f(x)}{g(x)+6}$ và $y=1$ bằng
| $2\ln3$ | |
| $\ln3$ | |
| $\ln18$ | |
| $2\ln2$ |
Cho hàm số $y=x^4-4x^2+m$. Tìm $m$ để đồ thị của hàm số cắt trục hoành tại $4$ điểm phân biệt sao cho hình phẳng giới hạn bởi đồ thị với trục hoành có diện tích phần phía trên trục hoành bằng diện tích phần phía dưới trục hoành. Khi đó $m=\dfrac{a}{b}$ với $\dfrac{a}{b}$ là phân số tối giản. Tính $a+2b$.
| $37$ | |
| $38$ | |
| $0$ | |
| $29$ |
Tính diện tích \(S\) của hình phẳng giới hạn bởi elip \((E)\) có phương trình \(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\), với \(a,\,b>0\).
| \(S=\pi\left(\dfrac{1}{a}+\dfrac{1}{b}\right)^2\) | |
| \(S=\pi(a+b)^2\) | |
| \(S=\pi ab\) | |
| \(S=\dfrac{\pi a^2b^2}{a+b}\) |
Đường gấp khúc $ABC$ trong hình vẽ bên là đồ thị của hàm số $y=f(x)$ trên đoạn $[-2;3]$.
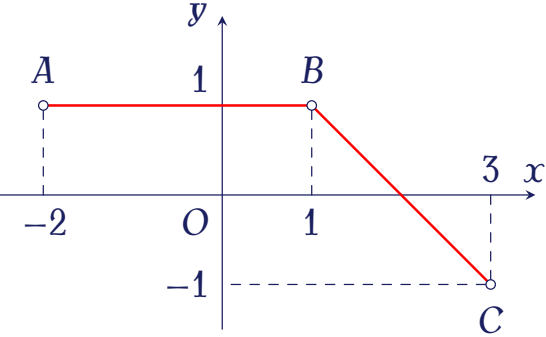
Tích phân $\displaystyle\displaystyle\int\limits_{-2}^3f(x)\mathrm{~d}x$ bằng
| $4$ | |
| $\dfrac{9}{2}$ | |
| $\dfrac{7}{2}$ | |
| $3$ |
Cho hàm số $y=f(x)$ có đạo hàm liên tục trên $\mathbb{R}$ và thỏa mãn $f(x)+x f'(x)=4x^3-6x^2$, $\forall x\in\mathbb{R}$. Diện tích hình phẳng giới hạn bởi các đường $y=f(x)$ và $y=f'(x)$ bằng
| $\dfrac{7}{12}$ | |
| $\dfrac{45}{4}$ | |
| $\dfrac{1}{2}$ | |
| $\dfrac{71}{6}$ |
Diện tích hình phẳng giới hạn bởi đồ thị của hàm số $y=x^5$, trục hoành và hai đường thẳng $x=-1$, $x=1$ bằng
| $\dfrac{3}{2}$ | |
| $\dfrac{1}{3}$ | |
| $7$ | |
| $5$ |
Cho hai hàm số $f(x)=mx^3+nx^2+px-\dfrac{5}{2}$ $(m,\,n,\,p\in\mathbb{R})$ và $g(x)=x^2+2x-1$ có đồ thị cắt nhau tại ba điểm có hoành độ lần lượt là $-3$, $-1$, $1$ (tham khảo hình vẽ).
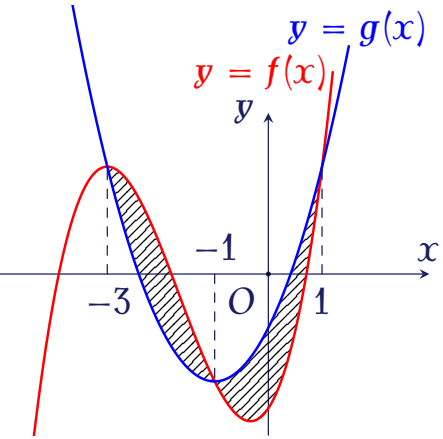
Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số $f(x)$ và $g(x)$ bằng
| $\dfrac{9}{2}$ | |
| $\dfrac{18}{5}$ | |
| $4$ | |
| $5$ |
Cho hàm số $y=f(x)$ có đạo hàm liên tục trên $\mathbb{R}$ và thỏa mãn $2f(x)+f'(x)=2x+1$, $\forall x\in\mathbb{R}$ và $f(0)=1$. Giá trị của $\displaystyle\int\limits_{0}^{1}f(x)\mathrm{\,d}x$ bằng
| $1-\dfrac{1}{2\mathrm{e}^2}$ | |
| $1+\dfrac{1}{2\mathrm{e}^2}$ | |
| $\dfrac{1}{2\mathrm{e}^2}$ | |
| $-\dfrac{1}{2\mathrm{e}^2}$ |
Cho hàm số $f(x)$ có đạo hàm $f'(x)$ liên tục trên $\mathbb{R}$ và thỏa mãn $\displaystyle\displaystyle\int\limits_{0}^{1}(3x+1)f'(x)\mathrm{\,d}x=2022$ và $4f(1)-f(0)=2028$. Giá trị của $I=\displaystyle\displaystyle\int\limits_{0}^{\tfrac{1}{4}}f(4x)\mathrm{\,d}x$ là
| $2$ | |
| $\dfrac{2022}{3}$ | |
| $\dfrac{1}{2}$ | |
| $\dfrac{1}{4}$ |
Cho hàm số $f(x)$ liên tục trên $(0;+\infty)$. Biết $\dfrac{1}{x^2}$ là một nguyên hàm của hàm số $y=f'(x)\ln x$ và $f(2)=\dfrac{1}{\ln2}$. Khi đó $\displaystyle\displaystyle\int\limits_{1}^{2}\dfrac{f(x)}{x}\mathrm{\,d}x$ bằng
| $-\dfrac{7}{4}$ | |
| $\dfrac{1}{2}$ | |
| $-\dfrac{1}{2}$ | |
| $\dfrac{7}{4}$ |
Biết $I=\displaystyle\displaystyle\int\limits_{1}^{2}\dfrac{\mathrm{d}x}{(x+1)\sqrt{x}+x\sqrt{x+1}}=\sqrt{a}-\sqrt{b}-c$ với $a,\,b,\,c$ là các số nguyên dương. Tính $P=a+b+c$.
| $P=18$ | |
| $P=12$ | |
| $P=24$ | |
| $P=46$ |
Diện tích hình phẳng giới hạn bởi đồ thị hàm số $y=x^2$ và đường thẳng $y=2x$ là
| $\dfrac{4}{3}$ | |
| $\dfrac{5}{3}$ | |
| $\dfrac{3}{2}$ | |
| $\dfrac{23}{15}$ |
Cho hàm số $y=f(x)$ liên tục trên $\mathbb{R}$. Gọi $S$ là diện tích hình phẳng giới hạn bởi đồ thị hàm số $y=f(x)$, trục hoành, đường thẳng $x=-1$, $x=5$ (như hình vẽ).
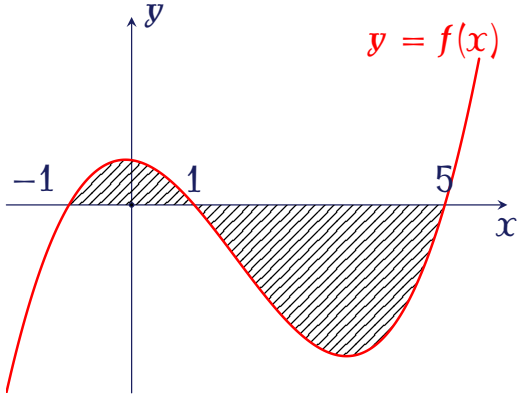
Mệnh đề nào sau đây đúng?
| $S=\displaystyle\displaystyle\int\limits_{-1}^{1}f(x)\mathrm{\,d}x+\displaystyle\int\limits_{1}^{5}f(x)\mathrm{\,d}x$ | |
| $S=-\displaystyle\displaystyle\int\limits_{-1}^{1}f(x)\mathrm{\,d}x-\displaystyle\int\limits_{1}^{5}f(x)\mathrm{\,d}x$ | |
| $S=\displaystyle\displaystyle\int\limits_{-1}^{1}f(x)\mathrm{\,d}x-\displaystyle\int\limits_{1}^{5}f(x)\mathrm{\,d}x$ | |
| $S=-\displaystyle\displaystyle\int\limits_{-1}^{1}f(x)\mathrm{\,d}x+\displaystyle\int\limits_{1}^{5}f(x)\mathrm{\,d}x$ |
Cho hàm số $y=f(x)$, $y=g(x)$ liên tục trên $[a;b]$. Gọi $H$ là hình phẳng giới hạn bởi đồ thị hàm số $y=f(x)$, $y=g(x)$, trục hoành và hai đường thẳng $x=a$, $x=b$ ($a< b$). Diện tích của hình $H$ được tính theo công thức nào sau đây?
| $S=\pi\displaystyle\displaystyle\int\limits_{a}^{b}\big[f(x)-g(x)\big]\mathrm{\,d}x$ | |
| $S=\displaystyle\displaystyle\int\limits_{a}^{b}\big|f(x)-g(x)\big|\mathrm{\,d}x$ | |
| $S=\pi\displaystyle\displaystyle\int\limits_{a}^{b}\big|f(x)-g(x)\big|\mathrm{\,d}x$ | |
| $S=\displaystyle\displaystyle\int\limits_{a}^{b}\big[f(x)-g(x)\big]\mathrm{\,d}x$ |
Cho hàm số $f(x)$ liên tục trên $\mathbb{R}$. Gọi $F(x),\,G(x)$ là hai nguyên hàm của $f(x)$ trên $\mathbb{R}$ thỏa mãn $F(4)+G(4)=4$ và $F(0)+G(0)=1$. Khi đó $\displaystyle\displaystyle\int_0^2f(2x)\mathrm{\,d}x$ bằng
| $3$ | |
| $\dfrac{3}{4}$ | |
| $6$ | |
| $\dfrac{3}{2}$ |
Một mảnh vườn hình elip có độ dài trục lớn $8$m và độ dài trục nhỏ $6$m. Người ta cần trồng rau trên dải đất rộng $4$m như hình vẽ.
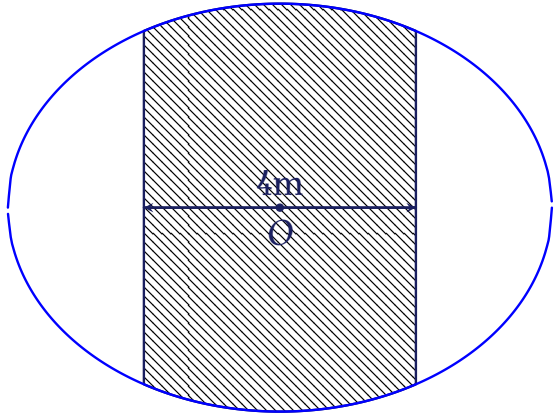
Hỏi cần bao nhiêu tiền để trồng rau trên dải đất đó, biết rằng kinh phí trồng rau là $70000$ đồng/m$^2$?
| $1.607.107$ đồng | |
| $803.553$ đồng | |
| $267.851$ đồng | |
| $2.638.938$ đồng |
Cho hàm số bậc bốn $y=f(x)$. Biết rằng hàm số $g(x)=\ln f(x)$ có bảng biến thiên như sau:
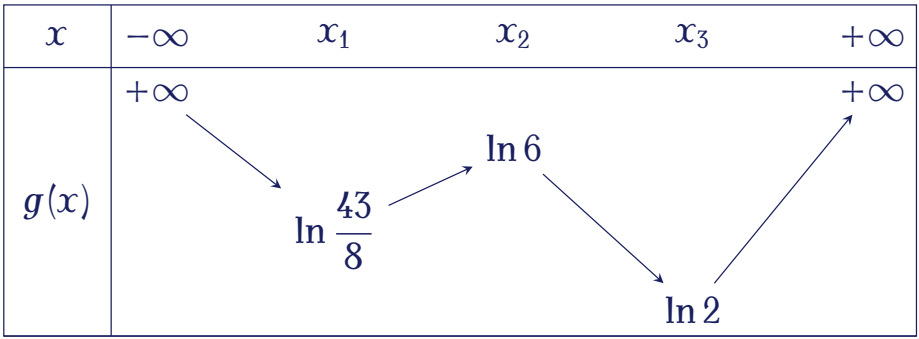
Diện tích hình phẳng giới hạn bởi các đường $y=f'(x)$ và $y=g'(x)$ thuộc khoảng nào dưới đây?
| $(5;6)$ | |
| $(4;5)$ | |
| $(2;3)$ | |
| $(3;4)$ |
