Tìm \(m\) để đường thẳng \(y=x-m\) cắt đồ thị hàm số \(y=\dfrac{2x+1}{x+1}\) tại \(2\) điểm phân biệt.
| \(m<-1\) | |
| \(m>-5\) | |
| \(m<-5\) hoặc \(m>-1\) | |
| \(-5< m<-1\) |
Tìm \(m\) để đường thẳng \(y=2x+m\) cắt đồ thị hàm số \(y=\dfrac{2x}{x+1}\) tại \(2\) điểm phân biệt.
| \(m\in(-\infty;0)\cup(8;+\infty)\) | |
| \(m\in(-\infty;0]\cup[8;+\infty)\) | |
| \(m\in(0;8)\) | |
| \(m\in[0;8]\) |
Gọi \(M\) và \(N\) là giao điểm của đồ thị hai hàm số \(y=x+1\) và \(y=\dfrac{2x+4}{x-1}\). Tìm hoành độ trung điểm \(I\) của đoạn thẳng \(MN\).
| \(x_I=-\dfrac{5}{2}\) | |
| \(x_I=2\) | |
| \(x_I=\dfrac{5}{2}\) | |
| \(x_I=1\) |
Cho hàm số $y=\dfrac{ax+b}{cx+1}$ ($a,\,b,\,c\in\mathbb{R}$) có đồ thị như hình bên.
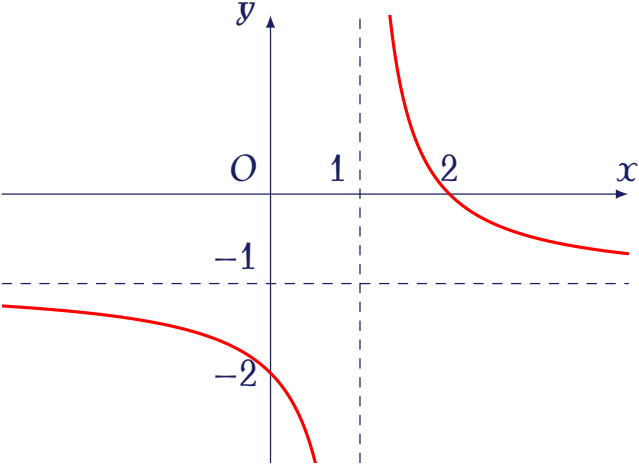
Khi đó $a+b-c$ bằng
| $-2$ | |
| $-1$ | |
| $1$ | |
| $0$ |
Đồ thị hàm số $y=\dfrac{x-4}{2x+2}$ cắt trục tung tại điểm có tung độ bằng
| $\dfrac{1}{2}$ | |
| $-1$ | |
| $-2$ | |
| $4$ |
Cho hàm số $y=\dfrac{ax+b}{cx+d}$ có đồ thị là đường cong trong hình bên.
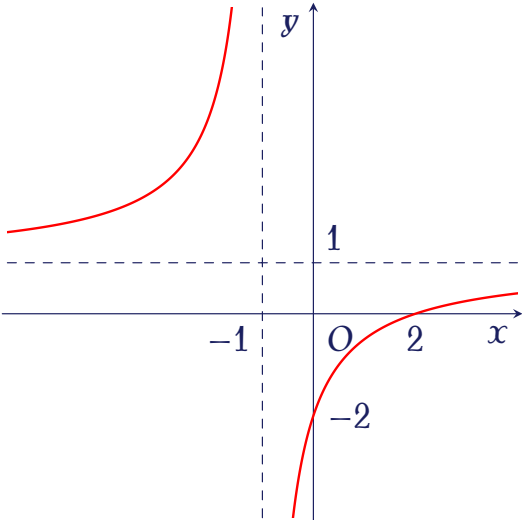
Tọa độ giao điểm của đồ thị hàm số đã cho và trục hoành là
| $(0;-2)$ | |
| $(2;0)$ | |
| $(-2;0)$ | |
| $(0;2)$ |
Cho hàm số $y=\dfrac{-x+1}{2x-1}$ có đồ thị $(\mathscr{C})$ và đường thẳng $(d)\colon y=x+m$. Với mọi giá trị thực của $m$ đường thẳng $(d)$ luôn cắt đồ thị $(\mathscr{C})$ tại hai điểm phân biệt $A$ và $B$. Gọi $k_1,\,k_2$ lần lượt là hệ số góc của các tiếp tuyến với $(\mathscr{C})$ tại $A$ và $B$. Giá trị nhỏ nhất của $T=k_1^{2022}+k_2^{2022}$ bằng
| $\dfrac{1}{2}$ | |
| $2$ | |
| $\dfrac{2}{3}$ | |
| $1$ |
Gọi $M$ và $m$ lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y=\dfrac{2x+3}{x-2}$ trên đoạn $[0;1]$. Tính giá trị $M+m$.
| $-2$ | |
| $\dfrac{7}{2}$ | |
| $-\dfrac{13}{2}$ | |
| $-\dfrac{17}{3}$ |
Cho hàm số $f(x)=\dfrac{ax-1}{bx+c}\,(a,\,b,\,c\in\mathbb{R})$ có bảng biến thiên như hình bên.
Giá trị của $a-b-c$ thuộc khoảnh nào sau đây?
| $\left(-1;0\right)$ | |
| $\left(-2;-1\right)$ | |
| $\left(1;2\right)$ | |
| $\left(0;1\right)$ |
Cho hàm số $y=x^4-4x^2+m$. Tìm $m$ để đồ thị của hàm số cắt trục hoành tại $4$ điểm phân biệt sao cho hình phẳng giới hạn bởi đồ thị với trục hoành có diện tích phần phía trên trục hoành bằng diện tích phần phía dưới trục hoành. Khi đó $m=\dfrac{a}{b}$ với $\dfrac{a}{b}$ là phân số tối giản. Tính $a+2b$.
| $37$ | |
| $38$ | |
| $0$ | |
| $29$ |
Đường thẳng nào sau đây tiếp xúc với parabol $\left(\mathscr{P}\right)\colon y=2x^2-5x+3$?
| $y=x+2$ | |
| $y=-x-1$ | |
| $y=x+3$ | |
| $y=-x+1$ |
Tọa độ giao điểm của parabol $\left(\mathscr{P}\right)\colon y=x^2-4x$ với đường thẳng $d\colon y=-x-2$ là
| $M(-1;-1)$, $N(-2;0)$ | |
| $M(1;-3)$, $N(2;-4)$ | |
| $M(0;-2)$, $N(2;-4)$ | |
| $M(-3;1)$, $N(3;-5)$ |
Tọa độ giao điểm của parabol $\left(P\right)\colon y=x^2-4x$ và đường thẳng $d\colon y=-x-2$ là
| $M\left(-1;-1\right)$, $N\left(-2;0\right)$ | |
| $M\left(1;-3\right)$, $N\left(2;-4\right)$ | |
| $M\left(0;-2\right)$, $N\left(2;-4\right)$ | |
| $M\left(-3;1\right)$, $N\left(3;-5\right)$ |
Biết rằng đồ thị hàm số $y=ax+b$ đi qua điểm $M\left(1;4\right)$ và song song với đường thẳng $y=2x+1$. Tính tổng $S=a+b$.
| $S=4$ | |
| $S=2$ | |
| $S=0$ | |
| $S=-4$ |
Điểm nào sau đây là điểm chung của parabol \(y=x^2-x+1\) và đường thẳng \(y=2x-1\)?
| \(P(3;5)\) | |
| \(N(2;3)\) | |
| \(M(1;-1)\) | |
| \(Q(0;1)\) |
Số giao điểm của đường cong \(y=x^3-2x^2+2x+1\) và đường thẳng \(y=1-x\) bằng
| \(0\) | |
| \(2\) | |
| \(1\) | |
| \(3\) |
Tìm tọa độ giao điểm \(M\) của đồ thị hàm số \(y=\dfrac{2x-1}{x+2}\) với trục tung.
| \(M\left(\dfrac{1}{2};0\right)\) | |
| \(M\left(0;2\right)\) | |
| \(M\left(0;-\dfrac{1}{2}\right)\) | |
| \(M\left(-\dfrac{1}{2};0\right)\) |
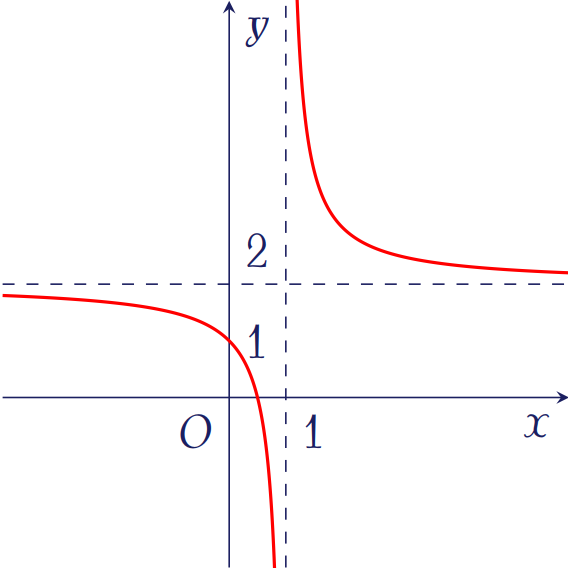
Cho hàm số \(y=\dfrac{ax-1}{bx+c}\) có đồ thị như hình trên. Tính giá trị biểu thức \(T=a+2b+3c\).
| \(T=1\) | |
| \(T=2\) | |
| \(T=3\) | |
| \(T=4\) |
Biết rằng đồ thị hàm số \(y=\dfrac{(m-2n-3)x+5}{x-m-n}\) nhận hai trục tọa độ làm hai đường tiệm cận. Tính tổng \(S=m^2+n^2-2\).
| \(S=2\) | |
| \(S=0\) | |
| \(S=-1\) | |
| \(S=1\) |
Biết rằng đồ thị hàm số \(y=\dfrac{ax+1}{bx-2}\) có đường tiệm cận đứng là \(x=2\) và đường tiệm cận ngang là \(y=3\). Tính giá trị của \(a+b\).
| \(a+b=1\) | |
| \(a+b=5\) | |
| \(a+b=4\) | |
| \(a+b=0\) |
