Cho khối chóp tứ giác đều $S.ABCD$ có cạnh đáy bằng $a$, cạnh bên hợp với đáy một góc $60^\circ$. Gọi $M$ là điểm đối xứng với $C$ qua $D$, $N$ là trung điểm $SC$. Mặt phẳng $(BMN)$ chia khối chóp thành hai khối đa diện. Tính thể tích $V$ của khối đa diện chứa đỉnh $C$.
| $V=\dfrac{7\sqrt{6}a^3}{72}$ | |
| $V=\dfrac{7\sqrt{6}a^3}{36}$ | |
| $V=\dfrac{5\sqrt{6}a^3}{36}$ | |
| $V=\dfrac{5\sqrt{6}a^3}{72}$ |
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông tại $A$, $\widehat{ABC}=30^\circ$. Tam giác $SBC$ là tam giác đều cạnh $a$ và nằm trong mặt phẳng vuông góc với đáy. Thể tích khối chóp $S.ABC$ là
| $\dfrac{3a^3}{16}$ | |
| $\dfrac{a^3}{16}$ | |
| $\dfrac{a^3\sqrt{3}}{16}$ | |
| $\dfrac{3\sqrt{3}a^3}{16}$ |
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành và có thể tích bằng $1$. Trên cạnh $SC$ lấy điểm $E$ sao cho $SE=2EC$. Tính thể tích $V$ của khối tứ diện $SEBD$.
| $V=\dfrac{1}{12}$ | |
| $V=\dfrac{1}{3}$ | |
| $V=\dfrac{1}{6}$ | |
| $V=\dfrac{2}{3}$ |
Cho hình chóp $S.ABCD$ có đáy là hình vuông cạnh $a$, $SA\perp(ABCD)$ và $SA=2a$. Thể tích của khối tứ diện $SBCD$ là
| $\dfrac{a^3}{3}$ | |
| $\dfrac{a^3}{4}$ | |
| $\dfrac{a^3}{6}$ | |
| $\dfrac{a^3}{8}$ |
Cho khối chóp tứ giác đều có chiều cao bằng $6$ và thể tích bằng $8$. Độ dài cạnh đáy bằng
| $3$ | |
| $\dfrac{2}{\sqrt{3}}$ | |
| $4$ | |
| $2$ |
Một khối chóp có thể tích $V=15\text{ cm}^3$ và chiều cao $h=3$m. Hỏi diện tích đáy của khối chóp đó là bao nhiêu?
| $15$m | |
| $5\text{ m}^2$ | |
| $5$m | |
| $15\text{ m}^2$ |
Cho khối chóp tứ giác đều $S.ABCD$ có cạnh đáy bằng $a$. Biết diện tích tứ giác $ABCD$ bằng ba lần diện tích tam giác $SAB$. Tính thể tích khối chóp đã cho.
| $\dfrac{a^3\sqrt{7}}{18}$ | |
| $\dfrac{a^3\sqrt{7}}{6}$ | |
| $\dfrac{a^3\sqrt{7}}{3}$ | |
| $\dfrac{a^3\sqrt{7}}{12}$ |
Cho khối chóp tứ giác $S.ABCD$ có thể tích $V$ và đáy là hình bình hành. Gọi $N$ là điểm trên cạnh $SD$ sao cho $ND=2NS$. Một mặt phẳng chứa $BN$ và song song với $AC$, cắt $SA$, $SC$ lần lượt tại $P,\,Q$. Gọi $V'$ là thể tích của khối chóp $S.BPNQ$. Khẳng định nào dưới đây đúng?
| $\dfrac{V'}{V}=\dfrac{1}{6}$ | |
| $\dfrac{V'}{V}=\dfrac{2}{5}$ | |
| $\dfrac{V'}{V}=\dfrac{1}{3}$ | |
| $\dfrac{V'}{V}=\dfrac{1}{4}$ |
Cho hình chóp $S.ABC$ có đáy là tam giác đều cạnh $a$. Hình chiếu của điểm $S$ trên mặt phẳng $(ABC)$ là điểm $H$ trên cạnh $AC$ thỏa mãn $AH=\dfrac{2}{3}AC$. Đường thẳng $SC$ tạo với mặt phẳng $(ABC)$ một góc bằng $60^\circ$. Thể tích của khối chóp $S.ABC$ bằng
| $\dfrac{a^3\sqrt{3}}{12}$ | |
| $\dfrac{a^3}{12}$ | |
| $\dfrac{a^3}{9}$ | |
| $\dfrac{a^3\sqrt{2}}{9}$ |
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông tại $A$, $AB=a$, $AC=2a$, $SA$ vuông góc với mặt phẳng đáy và $SB$ tạo với mặt đáy một góc $60^\circ$. Gọi $M,\,N$ lần lượt là trung điểm của $SB$ và $BC$. Thể tích khối chóp $A.SCNM$ bằng
| $\dfrac{\sqrt{3}}{4}a^3$ | |
| $\dfrac{\sqrt{3}}{2}a^3$ | |
| $\dfrac{3\sqrt{3}}{4}a^3$ | |
| $\dfrac{3\sqrt{3}}{2}a^3$ |
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a$, $SA$ vuông góc với mặt phẳng đáy và $SA=9a$. Thể tích khối chóp $S.ABCD$ bằng
| $a^3$ | |
| $27a^3$ | |
| $9a^3$ | |
| $3a^3$ |
Cho khối chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành, $SA=SB=SC=AC=a$, $SB$ tạo với mặt phẳng $(SAC)$ một góc $30^\circ$. Thể tích khối chóp đã cho bằng
| $\dfrac{a^3}{4}$ | |
| $\dfrac{a^3}{8}$ | |
| $\dfrac{\sqrt{3}a^3}{12}$ | |
| $\dfrac{\sqrt{3}a^3}{24}$ |
Cho khối chóp $S.ABCD$ có chiều cao bằng $4$ và đáy $ABCD$ có diện tích bằng $3$. Thể tích khối chóp đã cho bằng
| $7$ | |
| $5$ | |
| $4$ | |
| $12$ |
Nếu khối lăng trụ $ABC.A'B'C'$ có thể tích $V$ thì khối chóp $A'.ABC$ có thể tích bằng
| $\dfrac{V}{3}$ | |
| $V$ | |
| $\dfrac{2V}{3}$ | |
| $3V$ |
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $a$. Hình chiếu vuông góc của $S$ trên đáy là điểm $H$ trên cạnh $AC$ sao cho $AH=\dfrac{2}{3}AC$; mặt phẳng $(SBC)$ tạo với đáy một góc $60^{\circ}$. Thể tích khối chóp $S.ABC$ là
| $\dfrac{a^3\sqrt{3}}{12}$ | |
| $\dfrac{a^3\sqrt{3}}{48}$ | |
| $\dfrac{a^3\sqrt{3}}{36}$ | |
| $\dfrac{a^3\sqrt{3}}{24}$ |
Cho khối chóp có diện tích đáy $B=2a^2$ và chiều cao $h=9a$. Thể tích của khối chóp đã cho bằng
| $9a^3$ | |
| $6a^3$ | |
| $3a^3$ | |
| $18a^3$ |
Cho khối chóp $S.ABC$ có đáy là tam giác vuông cân tại $A$, $AB=2$, $SA$ vuông góc với đáy và $SA=3$ (tham khảo hình bên).
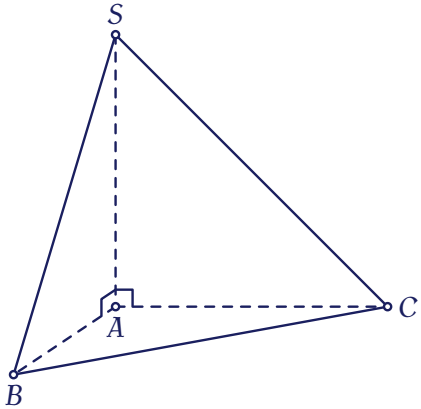
Thể tích khối chóp đã cho bằng
| $12$ | |
| $2$ | |
| $6$ | |
| $4$ |
Cho tứ diện $ABCD$, trên các cạnh $BC$, $BD$, $AC$ lần lượt lấy các điểm $M,\,N,\,P$ sao cho $BC=3BM$, $BD=\dfrac{3}{2}BN$, $AC=2AP$. Mặt phẳng $(MNP)$ chia khối tứ diện $ABCD$ thành hai khối đa diện có thể tích là $V_1$, $V_2$, trong đó khối đa diện chứa cạnh $CD$ có thể tích là $V_2$. Tính tỉ số $\dfrac{V_1}{V_2}$.
| $\dfrac{V_1}{V_2}=\dfrac{26}{19}$ | |
| $\dfrac{V_1}{V_2}=\dfrac{26}{13}$ | |
| $\dfrac{V_1}{V_2}=\dfrac{3}{19}$ | |
| $\dfrac{V_1}{V_2}=\dfrac{15}{19}$ |
Cho khối chóp có diện tích đáy $B=6a^2$ và chiều cao $h=2a$. Thể tích khối chóp đã cho bằng
| $12a^3$ | |
| $6a^3$ | |
| $4a^3$ | |
| $2a^3$ |
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $a$, tam giác $SAB$ đều và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp $S.ABC$.
| $\dfrac{a^3\sqrt{3}}{18}$ | |
| $\dfrac{a^3\sqrt{3}}{12}$ | |
| $\dfrac{a^3}{8}$ | |
| $\dfrac{a^3}{6}$ |
