Đạo hàm của hàm số $y=x^{2023}$ là
| $y'=2023x^{2023}$ | |
| $y'=2022x^{2023}$ | |
| $y'=2023x^{2022}$ | |
| $y'=\dfrac{1}{2023}x^{2022}$ |
Đạo hàm của hàm số $y=\big(x^4+3\big)^{\tfrac{1}{3}}$ là
| $y'=\dfrac{4}{3}x^3\big(x^4+3\big)^{-\tfrac{2}{3}}$ | |
| $y'=\dfrac{1}{3}x^3\big(x^4+3\big)^{-\tfrac{2}{3}}$ | |
| $y'=\dfrac{4}{3}x^3\big(x^4+3\big)^{\tfrac{2}{3}}$ | |
| $y'=4x^3\big(x^4+3\big)^{-\tfrac{2}{3}}$ |
Trên khoảng $(0;+\infty)$, đạo hàm của hàm số $y=x^{\pi}$ là
| $y'=\pi x^{\pi-1}$ | |
| $y'=x^{\pi-1}$ | |
| $y'=\dfrac{1}{\pi}x^{\pi-1}$ | |
| $y'=\pi x^{\pi}$ |
Đạo hàm của hàm số $y=\big(x^4+3\big)^{\tfrac{1}{3}}$ là
| $y'=\dfrac{4}{3}x^3\big(x^4+3\big)^{-\tfrac{2}{3}}$ | |
| $y'=\dfrac{1}{3}x^3\big(x^4+3\big)^{-\tfrac{2}{3}}$ | |
| $y'=\dfrac{4}{3}x^3\big(x^4+3\big)^{\tfrac{2}{3}}$ | |
| $y'=4x^3\big(x^4+3\big)^{-\tfrac{2}{3}}$ |
Đạo hàm của hàm số $y=x^{-3}$ là
| $y'=-x^{-4}$ | |
| $y'=-\dfrac{1}{2}x^{-2}$ | |
| $y'=-\dfrac{1}{3}x^{-4}$ | |
| $y'=-3x^{-4}$ |
Trên khoảng $(0;+\infty)$, đạo hàm của hàm số $y=x^{\tfrac{5}{2}}$ là
| $y'=\dfrac{2}{7}x^{\tfrac{7}{2}}$ | |
| $y'=\dfrac{2}{5}x^{\tfrac{3}{2}}$ | |
| $y'=\dfrac{5}{2}x^{\tfrac{3}{2}}$ | |
| $y'=\dfrac{5}{2}x^{-\tfrac{3}{2}}$ |
Tìm đạo hàm của hàm số $$y=\left(x^2-x+1\right)^{\tfrac{1}{3}}$$
| \(y'=\dfrac{2x-1}{\sqrt[3]{\left(x^2-x+1\right)^2}}\) | |
| \(y'=\dfrac{1}{3\sqrt[3]{\left(x^2-x+1\right)^2}}\) | |
| \(y'=\dfrac{2x-1}{3\sqrt[3]{x^2-x+1}}\) | |
| \(y'=\dfrac{2x-1}{3\sqrt[3]{\left(x^2-x+1\right)^2}}\) |
Tập xác định của hàm số $y=x^{\sqrt{2}-1}$ là
| $\big(-\infty;\sqrt{2}\big)$ | |
| $\mathbb{R}\setminus\{0\}$ | |
| $\mathbb{R}$ | |
| $(0;+\infty)$ |
Cho hàm số $y=\big(2x^2-1\big)^{\tfrac{1}{2}}$. Giá trị của hàm số đã cho tại điểm $x=2$ bằng
| $3$ | |
| $\sqrt{7}$ | |
| $\sqrt{3}$ | |
| $7$ |
Tập xác định của hàm số $y=(x+2)^{-2022}$ là
| $[-2;+\infty)$ | |
| $(-2;+\infty)$ | |
| $\mathbb{R}\setminus\{-2\}$ | |
| $\mathbb{R}$ |
Cho hàm số $f(x)=\big(1-\sqrt[4]{x}\big)\big(1+\sqrt[4]{x}\big)\big(1+\sqrt{x}\big)(1+x)$. Tính $f\left(\dfrac{1}{2^{64}}\right)$.
| $1-\dfrac{1}{2^{128}}$ | |
| $1+\dfrac{1}{2^{64}}$ | |
| $1+\dfrac{1}{2^{128}}$ | |
| $1-\dfrac{1}{2^{64}}$ |
Cho đồ thị các hàm số $y=x^\alpha$ và $y=x^\beta$ trên khoảng $(0;+\infty)$.
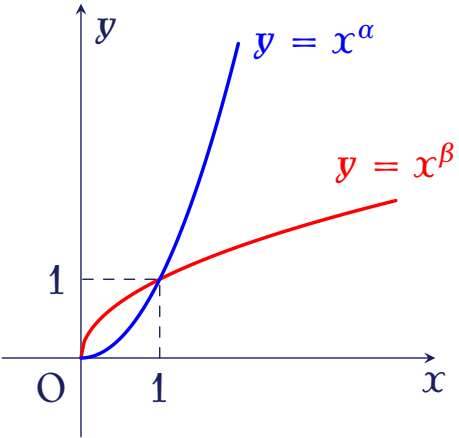
Mệnh đề nào dưới đây đúng?
| $0< \alpha< 1< \beta$ | |
| $\alpha< 0< 1< \beta$ | |
| $0< \beta< 1< \alpha$ | |
| $\beta< 0< 1< \alpha$ |
Tập xác định của hàm số $y=x^{-\pi}$ là
| $\left(-\infty;0\right)$ | |
| $\mathbb{R}\setminus\{0\}$ | |
| $\left[0;+\infty\right)$ | |
| $\left(0;+\infty\right)$ |
Tập xác định của hàm số $y=x^{\sqrt{2}}$ là
| $\mathbb{R}$ | |
| $\mathbb{R}\setminus\{0\}$ | |
| $(0;+\infty)$ | |
| $(2;+\infty)$ |
Trên khoảng $(0;+\infty)$, họ nguyên hàm của hàm số $f(x)=x^{\tfrac{3}{2}}$ là
| $\displaystyle\displaystyle\int f(x)\mathrm{\,d}x=\dfrac{3}{2}x^{\tfrac{1}{2}}+C$ | |
| $\displaystyle\displaystyle\int f(x)\mathrm{\,d}x=\dfrac{5}{2}x^{\tfrac{2}{5}}+C$ | |
| $\displaystyle\displaystyle\int f(x)\mathrm{\,d}x=\dfrac{2}{5}x^{\tfrac{5}{2}}+C$ | |
| $\displaystyle\displaystyle\int f(x)\mathrm{\,d}x=\dfrac{2}{3}x^{\tfrac{1}{2}}+C$ |
Tập xác định \(\mathscr{D}\) của hàm số \(y=(x+1)^{\tfrac{1}{3}}\) là
| \(\mathscr{D}=\mathbb{R}\setminus\{-1\}\) | |
| \(\mathscr{D}=(-1;+\infty)\) | |
| \(\mathscr{D}=\mathbb{R}\) | |
| \(\mathscr{D}=(-\infty;-1)\) |
Cho các số thực \(\alpha\) và \(\beta\). Đồ thị các hàm số \(y=x^\alpha\) và \(y=x^\beta\) trên khoảng \((0;+\infty)\) như hình vẽ.
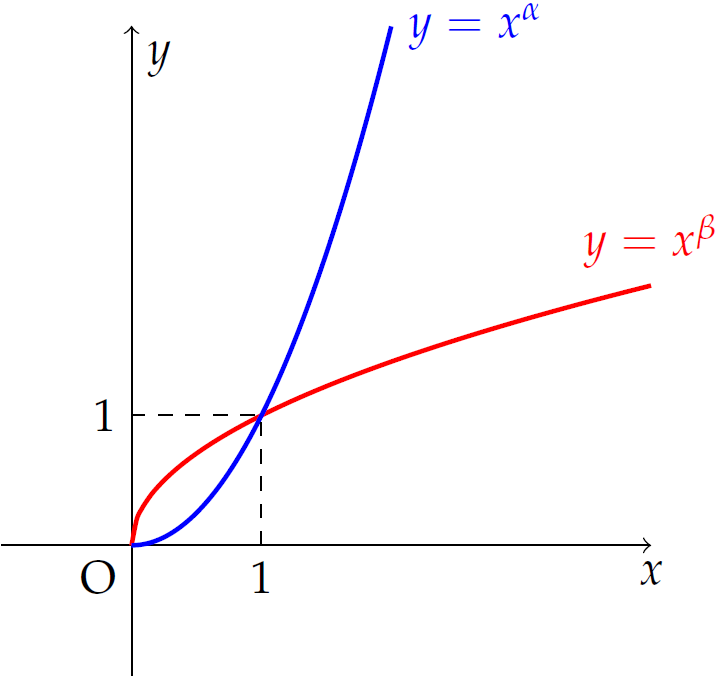
Mệnh đề nào dưới đây đúng?
| \(0< \beta<\alpha<1\) | |
| \(\alpha< 0<\beta<1\) | |
| \(0< \beta< 1<\alpha\) | |
| \(\beta< 0< 1<\alpha\) |
Cho hàm số \(f(x)=\left(2x^2+3x+1\right)^{\tfrac{3}{2}}\). Khi đó giá trị của \(f(1)\) bằng
| \(8\) | |
| \(\dfrac{3}{2}\) | |
| \(6\sqrt{6}\) | |
| \(6^{\tfrac{2}{3}}\) |
Tìm tập xác định \(\mathscr{D}\) của hàm số \(y=(1-x)^{\sqrt{2}}\).
| \(\mathscr{D}=(1;+\infty)\) | |
| \(\mathscr{D}=\Bbb{R}\setminus\{1\}\) | |
| \(\mathscr{D}=(-\infty;1)\) | |
| \(\mathscr{D}=\Bbb{R}\) |
Tìm tập xác định \(\mathscr{D}\) của hàm số \(y=(x-1)^{\tfrac{1}{2}}\).
| \(\mathscr{D}=(0;+\infty)\) | |
| \(\mathscr{D}=[1;+\infty)\) | |
| \(\mathscr{D}=(1;+\infty)\) | |
| \(\mathscr{D}=\Bbb{R}\) |
