Đồ thị của hàm số nào dưới đây cắt trục hoành tại $3$ điểm phân biệt?
| $y=x^3-3x+3$ | |
| $y=x^3+3x+1$ | |
| $y=-x^3+3x+5$ | |
| $y=x^3-3x+1$ |
Tìm các giá trị của tham số \(m\) để đường cong \(\left(\mathscr{C}\right)\colon y=x^3-3x+m\) cắt trục hoành tại \(3\) điểm phân biệt.
| \(m\in(2;+\infty)\) | |
| \(m\in(-2;2)\) | |
| \(m\in\mathbb{R}\) | |
| \(m\in(-\infty;-2)\) |
Số giao điểm của đồ thị hàm số \(y=-2x^3-3x^2+1\) với trục hoành là
| \(1\) | |
| \(0\) | |
| \(3\) | |
| \(2\) |
Tính diện tích \(S\) của hình phẳng \((H)\) giới hạn bởi đồ thị hàm số \(y=-x^3+3x^2-2\), hai trục tọa độ và đường thẳng \(x=2\).
| \(S=\dfrac{1}{3}\) | |
| \(S=\dfrac{19}{2}\) | |
| \(S=\dfrac{9}{2}\) | |
| \(S=\dfrac{5}{2}\) |
Số giao điểm của đồ thị hàm số \(y=x^3-3x+1\) và trục hoành là
| \(3\) | |
| \(0\) | |
| \(2\) | |
| \(1\) |
Tập hợp các tham số thực \(m\) để đồ thị của hàm số \(y=x^3+(m-4)x+2m\) cắt trục hoành tại ba điểm phân biệt là
| \((-\infty;1]\setminus\{-8\}\) | |
| \((-\infty;1)\setminus\{-8\}\) | |
| \((-\infty;1]\) | |
| \((-\infty;1)\) |
Cho hàm số bậc ba $y=f(x)$ có đồ thị là đường cong trong hình bên.
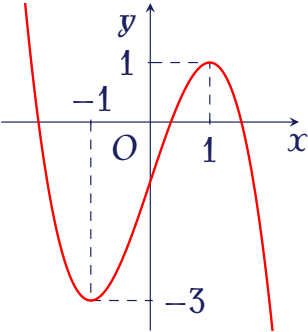
Có bao nhiêu giá trị nguyên của tham số $m$ để phương trình $f(x)=m$ có ba nghiệm thực phân biệt?
| $2$ | |
| $5$ | |
| $3$ | |
| $4$ |
Cho hàm số $y=\dfrac{ax+b}{cx+d}$ có đồ thị là đường cong trong hình bên.
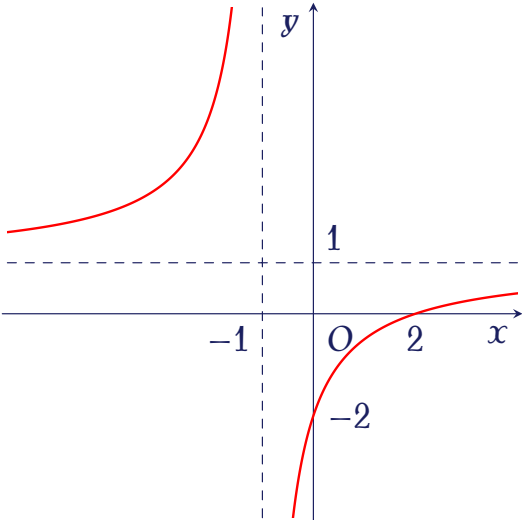
Tọa độ giao điểm của đồ thị hàm số đã cho và trục hoành là
| $(0;-2)$ | |
| $(2;0)$ | |
| $(-2;0)$ | |
| $(0;2)$ |
Cho hàm số $f(x)=x^3+ax^2+bx+c$ có đồ thị $\left(\mathscr{C}\right)$. Mệnh đề nào sau đây sai?
| Đồ thị $\left(\mathscr{C}\right)$ luôn có tâm đối xứng | |
| Hàm số $f(x)$ luôn có cực trị | |
| Đồ thị $\left(\mathscr{C}\right)$ luôn cắt trục hoành | |
| $\lim\limits_{x\to+\infty}f(x)=+\infty$ |
Cho hàm số bậc ba $y=f(x)$ có đồ thị là đường cong trong hình bên.
Số nghiệm thực phân biệt của phương trình $f\big(f(x)\big)=1$ là
| $9$ | |
| $3$ | |
| $6$ | |
| $7$ |
Cho hàm số $y=x^4-4x^2+m$. Tìm $m$ để đồ thị của hàm số cắt trục hoành tại $4$ điểm phân biệt sao cho hình phẳng giới hạn bởi đồ thị với trục hoành có diện tích phần phía trên trục hoành bằng diện tích phần phía dưới trục hoành. Khi đó $m=\dfrac{a}{b}$ với $\dfrac{a}{b}$ là phân số tối giản. Tính $a+2b$.
| $37$ | |
| $38$ | |
| $0$ | |
| $29$ |
Đồ thị của hàm số $y=x^3-3x+2$ cắt trục tung tại điểm có tung độ bằng
| $0$ | |
| $1$ | |
| $2$ | |
| $-2$ |
Parabol $\left(\mathscr{P}\right)\colon y=x^2+4x+4$ có số điểm chung với trục hoành là
| $0$ | |
| $1$ | |
| $2$ | |
| $3$ |
Tìm các giá trị của tham số \(m\) để phương trình \(x^3-12x+m-2=0\) có \(3\) nghiệm phân biệt.
| \(m\in[-14;18]\) | |
| \(m\in(-14;18)\) | |
| \(m\in(-18;14)\) | |
| \(\left[\begin{array}{l}m<-14\\ m>18\end{array}\right.\) |
Số giao điểm của đường cong \(y=x^3-2x^2+2x+1\) và đường thẳng \(y=1-x\) bằng
| \(0\) | |
| \(2\) | |
| \(1\) | |
| \(3\) |
Đồ thị của hai hàm số \(y=-x^3+3x^2+2x-1\) và \(y=3x^2-2x-1\) có tất cả bao nhiêu điểm chung?
| \(1\) | |
| \(2\) | |
| \(0\) | |
| \(3\) |
Đồ thị hàm số \(y=x^4+3x^2-4\) cắt trục hoành tại bao nhiêu điểm?
| \(4\) | |
| \(2\) | |
| \(3\) | |
| \(0\) |
Số giao điểm của đồ thị hàm số \(y=x^4-5x^2+4\) với trục hoành là
| \(3\) | |
| \(2\) | |
| \(4\) | |
| \(1\) |
Cho hàm số \(y=x(1-x)\left(x^2+1\right)\) có đồ thị \(\left(\mathscr{C}\right)\). Mệnh đề nào sau đây là đúng?
| \(\left(\mathscr{C}\right)\) không cắt trục hoành | |
| \(\left(\mathscr{C}\right)\) cắt trục hoành tại \(3\) điểm | |
| \(\left(\mathscr{C}\right)\) cắt trục hoành tại \(1\) điểm | |
| \(\left(\mathscr{C}\right)\) cắt trục hoành tại \(2\) điểm |
Cho hàm số \(y=(x-2)\left(x^2-5x+6\right)\) có đồ thị \(\left(\mathscr{C}\right)\). Mệnh đề nào sau đây là đúng?
| \(\left(\mathscr{C}\right)\) không cắt trục hoành | |
| \(\left(\mathscr{C}\right)\) cắt trục hoành tại \(3\) điểm | |
| \(\left(\mathscr{C}\right)\) cắt trục hoành tại \(1\) điểm | |
| \(\left(\mathscr{C}\right)\) cắt trục hoành tại \(2\) điểm |
