Gọi $x_1,\,x_2$ là các điểm cực trị của hàm số $y=x^3-2x^2-7x+1$. Tính $x_1^2+x_2^2$.
| $\dfrac{44}{9}$ | |
| $\dfrac{16}{3}$ | |
| $\dfrac{28}{3}$ | |
| $\dfrac{58}{9}$ |
Đồ thị hàm số \(y=x^3-2mx^2+m^2x+n\) có tọa độ điểm cực tiểu là \((1;3)\). Khi đó \(m+n\) bằng
| \(4\) | |
| \(3\) | |
| \(2\) | |
| \(1\) |
Hàm số \(y=x^3-9x^2+1\) có hai điểm cực trị là \(x_1,\,x_2\). Tính \(x_1+x_2\).
| \(6\) | |
| \(-10\) | |
| \(0\) | |
| \(-107\) |
Hàm số $y=\dfrac{1}{3}x^3-mx^2+\big(m^2-m-1\big)x+m^3$ đạt cực đại tại điểm $x=1$ thì giá trị của tham số $m$ bằng
| $\left[\begin{array}{l}m=0\\ m=3\end{array}\right.$ | |
| $m=0$ | |
| $m=-3$ | |
| $m=3$ |
Biết đồ thị của hàm số $f(x)=ax^3+bx^2+cx+d$ có hai điểm cực trị là $A(1;1)$ và $B\left(2;\dfrac{4}{3}\right)$. Tính $f(-1)$.
| $12$ | |
| $7$ | |
| $\dfrac{31}{3}$ | |
| $\dfrac{16}{3}$ |
Đồ thị của hàm số nào dưới đây có đúng một điểm cực trị?
| $y=x^3-2x^2-1$ | |
| $y=-x^4+2x^2-1$ | |
| $y=x^4-2x^2-1$ | |
| $y=x^4+2x^2+1$ |
Có bao nhiêu giá trị nguyên của tham số $m$ sao cho ứng với mỗi $m$, hàm số $y=-x^3+3x^2-3mx+\dfrac{5}{3}$ có đúng một cực trị thuộc khoảng $(-2;5)$?
| $16$ | |
| $6$ | |
| $17$ | |
| $7$ |
Cho hàm số bậc ba $y=f(x)$ có đồ thị là đường cong trong hình bên.
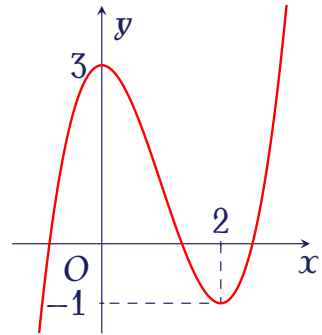
Giá trị cực đại của hàm số đã cho là
| $-1$ | |
| $3$ | |
| $2$ | |
| $0$ |
Trong các hàm số sau, hàm số nào không có cực trị?
| $y=x^2$ | |
| $y=\dfrac{x+2}{2x-1}$ | |
| $y=x^4+2x^2+2$ | |
| $y=-x^3-x^2$ |
Biết đồ thị của hàm số $f(x)=ax^3+bx^2+cx+d$ có hai điểm cực trị là $A(1;1)$ và $B\left(2;\dfrac{4}{3}\right)$. Tính $f(-1)$.
| $12$ | |
| $7$ | |
| $\dfrac{31}{3}$ | |
| $\dfrac{16}{3}$ |
Tìm các điểm cực trị hàm số $f(x)=x^3-3x+1$.
Cho hàm số $f(x)=x^3+ax^2+bx+c$ có đồ thị $\left(\mathscr{C}\right)$. Mệnh đề nào sau đây sai?
| Đồ thị $\left(\mathscr{C}\right)$ luôn có tâm đối xứng | |
| Hàm số $f(x)$ luôn có cực trị | |
| Đồ thị $\left(\mathscr{C}\right)$ luôn cắt trục hoành | |
| $\lim\limits_{x\to+\infty}f(x)=+\infty$ |
Số điểm cực trị của hàm số $y=\dfrac{1}{3}x^3-2x^2+4$ là
| $0$ | |
| $1$ | |
| $2$ | |
| $3$ |
Giá trị cực tiểu $y_{CT}$ của hàm số $y=x^3-3x^2+2$ là
| $y_{CT}=0$ | |
| $y_{CT}=-2$ | |
| $y_{CT}=1$ | |
| $y_{CT}=4$ |
Gọi $x_1,\,x_2$ là hai điểm cực trị của hàm số $y=4x^3+mx^2-3x$. Tìm các giá trị của tham số $m$ sao cho $x_1+4x_2=0$.
| $m=0$ | |
| $m=\pm\dfrac{9}{2}$ | |
| $m=\pm\dfrac{3}{2}$ | |
| $m=\pm\dfrac{1}{2}$ |
Gọi $x_1,\,x_2$ là hai điểm cực trị của hàm số $y=x^3-3mx^2+3\big(m^2-1\big)x-m^3+m$. Tìm các giá trị của tham số $m$ sao cho $x_1^2+x_2^2-x_1x_2=7$.
| $m=0$ | |
| $m=\pm\dfrac{9}{2}$ | |
| $m=\pm\dfrac{1}{2}$ | |
| $m=\pm2$ |
Gọi $S$ là tập hợp các giá trị nguyên để hàm số $y=\dfrac{x^3}{3}-(m+1)x^2+(m-2)x+2m-3$ đạt cực trị tại hai điểm $x_1,\,x_2$ thỏa mãn $x_1^2+x_2^2=18$. Tính tổng $P$ của tất cả các giá trị $m$ trong $S$.
| $P=-4$ | |
| $P=1$ | |
| $P=-\dfrac{3}{2}$ | |
| $P=-5$ |
Đồ thị hàm số $y=x^3-3x^2-9x+1$ có hai điểm cực trị là $A$ và $B$. Điểm nào sau đây thuộc đường thẳng $AB$?
| $M(0;-1)$ | |
| $Q(-1;10)$ | |
| $P(1;0)$ | |
| $N(1;-10)$ |
Viết phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số $y=-2x^3+3x^2+1$.
| $y=x+1$ | |
| $y=-x+1$ | |
| $y=x-1$ | |
| $y=-x-1$ |
Biết đồ thị hàm số $y=x^3-3x+1$ có hai điểm cực trị $A,\,B$. Khi đó đường thẳng $AB$ có phương trình
| $y=2x-1$ | |
| $y=x-2$ | |
| $y=-x+2$ | |
| $y=-2x+1$ |
