Tìm tất cả các giá trị thực của tham số $m$ để hàm số $y=\ln\big(x^2-2x+m+1\big)$ có tập xác định là $\mathbb{R}$.
| $m=0$ | |
| $m< -1$ hoặc $m>0$ | |
| $m>0$ | |
| $0< m< 3$ |
Tìm tất cả các giá trị thực của tham số $m$ để hàm số $y=\log_2\left(x^2-2x+m\right)$ có tập xác định là $\mathbb{R}$.
| $m\geq1$ | |
| $m\leq1$ | |
| $m>1$ | |
| $m< -1$ |
Cho hàm số $f\left(x\right)=\log_2^3x-\log_2x^3+m$ ($m$ là tham số thực). Gọi $S$ là tập hợp tất cả các giá trị của $m$ sao cho $\max\limits_{\left[1;4\right]}\left|f\left(x\right)\right|+\min\limits_{\left[1;4\right]}\left|f\left(x\right)\right|=6$. Tổng bình phương các phần tử của $S$ bằng
| $13$ | |
| $18$ | |
| $5$ | |
| $8$ |
Kết quả của phép tính tích phân \(\displaystyle\int\limits_{0}^{1}\ln(2x+1)\mathrm{\,d}x=a\ln3+b\), (\(a,\,b\in\mathbb{Q}\)) khi đó giá trị của \(ab^3\) bằng
| \(-\dfrac{3}{2}\) | |
| \(3\) | |
| \(1\) | |
| \(\dfrac{3}{2}\) |
Tập hợp các giá trị thực của tham số \(m\) để phương trình \(\log_2x=m\) có nghiệm là
| \((0;+\infty)\) | |
| \([0;+\infty)\) | |
| \((-\infty;0)\) | |
| \(\mathbb{R}\) |
Có bao nhiêu giá trị nguyên dương của tham số $m$ để hàm số $y=\dfrac{3}{4}x^4-(m-1)x^2-\dfrac{1}{4x^4}$ đồng biến trên khoảng $(0;+\infty)$?
| $4$ | |
| $2$ | |
| $1$ | |
| $3$ |
Cho hàm số bậc bốn $y=f(x)$ có đồ thị là đường cong như hình vẽ bên dưới.
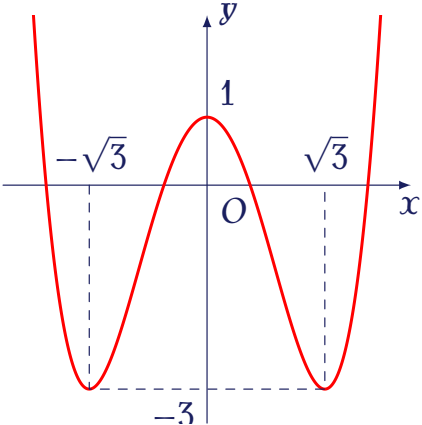
Có bao nhiêu giá trị nguyên âm của tham số $m$ để phương trình $f(x)=m$ có bốn nghiệm thực phân biệt?
| $3$ | |
| $2$ | |
| $4$ | |
| $5$ |
Hàm số $y=\dfrac{1}{3}x^3-mx^2+\big(m^2-m-1\big)x+m^3$ đạt cực đại tại điểm $x=1$ thì giá trị của tham số $m$ bằng
| $\left[\begin{array}{l}m=0\\ m=3\end{array}\right.$ | |
| $m=0$ | |
| $m=-3$ | |
| $m=3$ |
Tìm tập xác định của hàm số $y=\log_{2023}\big(3x-x^2\big)$.
| $\mathscr{D}=(0;+\infty)$ | |
| $\mathscr{D}=(-\infty;0)\cup(3;+\infty)$ | |
| $\mathscr{D}=\mathbb{R}$ | |
| $\mathscr{D}=(0;3)$ |
Cho hàm số $f(x)=\ln\big(x^2+1\big)$. Giá trị $f'(2)$ bằng
| $\dfrac{4}{5}$ | |
| $\dfrac{4}{3\ln2}$ | |
| $\dfrac{4}{2\ln5}$ | |
| $2$ |
Có tât cả bao nhiêu giá trị nguyên của tham số $m$ để hàm số $y=\dfrac{1}{3}x^3-mx^2+9x-1$ đồng biến trên $\mathbb{R}$?
| $8$ | |
| $9$ | |
| $7$ | |
| $6$ |
Tìm tập hợp tất cả các giá trị thực của tham số $m$ sao cho đồ thị hàm số $y=x^4-2mx^2+2m^4-m$ có $3$ điểm cực trị đều nằm trên các trục tọa độ.
| $\big\{0;1\big\}$ | |
| $\big\{1\big\}$ | |
| $\big\{-1;1\big\}$ | |
| $\big\{0\big\}$ |
Đạo hàm của hàm số $y=\dfrac{\ln2x}{x}$ là
| $y'=\dfrac{1-\ln2x}{x^2}$ | |
| $y'=\dfrac{\ln2x}{2x}$ | |
| $y'=\dfrac{\ln2x}{x^2}$ | |
| $y'=\dfrac{1}{2x}$ |
Tập xác định của hàm số $y=\log_{\sqrt{3}}x$ là
| $[0;+\infty)$ | |
| $(0;+\infty)$ | |
| $(-\infty;0)$ | |
| $\mathbb{R}$ |
Số giá trị nguyên của tham số $m$ để hàm số $y=(m+2)x^4+(m-3)x^2+2022$ có ba cực trị là
| $4$ | |
| $2$ | |
| $3$ | |
| $6$ |
Số giá trị nguyên của tham số $m$ để hàm số $y=x^3-(m+1)x^2+3x+1$ đồng biến trên $\mathbb{R}$ là
| $4$ | |
| $6$ | |
| $5$ | |
| $7$ |
Cho hàm số $f(x)=ax^3+bx^2+cx+d$ ($a\neq0$) có đồ thị là đường cong trong hình bên.
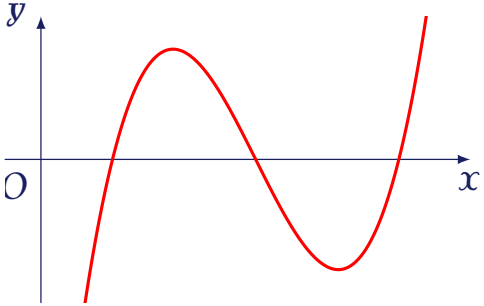
Số các giá trị nguyên của tham số $m\in(-2019;2023]$ để phương trình $4^{f(x)}-(m-1)2^{f(x)+1}+2m-3=0$ có đúng ba nghiệm là
| $2020$ | |
| $2019$ | |
| $2021$ | |
| $2022$ |
Giá trị của tham số $m$ sao cho tiệm cận ngang của đồ thị hàm số $y=\dfrac{mx+5}{x+1}$ đi qua điểm $M(2;-4)$ là
| $4$ | |
| $-4$ | |
| $-2$ | |
| $2$ |
Tập xác định của hàm số $y=\log_{2022}(2x-1)$ là
| $[0;+\infty)$ | |
| $\left(\dfrac{1}{2};+\infty\right)$ | |
| $\left[\dfrac{1}{2};+\infty\right)$ | |
| $(0;+\infty)$ |
Đạo hàm của hàm số $y=\ln\big(x^2+2\big)$ là
| $y'=\dfrac{1}{x^2+2}$ | |
| $y'=\dfrac{x}{x^2+2}$ | |
| $y'=\dfrac{2}{x^2+2}$ | |
| $y'=\dfrac{2x}{x^2+2}$ |
