Cho hình lăng trụ đứng $ABC.A'B'C'$ có đáy $ABC$ là tam giác vuông cân tại $A$ với $AC=4a$ và mặt bên $AA'B'B$ là hình vuông. Thể tích của khối lăng trụ $ABC.A'B'C'$ bằng
| $\dfrac{a^3}{8}$ | |
| $64a^3$ | |
| $\dfrac{a^3}{4}$ | |
| $32a^3$ |
Cho khối hộp chữ nhật $ABCD.A'B'C'D'$ có đáy hình vuông. $BD=2a$, góc giữa hai mặt phẳng $\left(A'BD\right)$ và $(ABCD)$ bằng $30^\circ$. Thể tích của khối hộp chữ nhật đã cho bằng
| $6\sqrt{3}a^3$ | |
| $\dfrac{2\sqrt{3}}{9}a^3$ | |
| $2\sqrt{3}a^3$ | |
| $\dfrac{2\sqrt{3}}{3}a^3$ |
Một tấm bìa hình vuông có cạnh $44$cm, người ta cắt bỏ đi ở mỗi góc tấm bìa một hình vuông cạnh $12$cm rồi gấp lại thành một cái hộp chữ nhật không có nắp. Tính thể tích cái hộp này.
| $4800$cm$^3$ | |
| $9600$cm$^3$ | |
| $2400$cm$^3$ | |
| $2400\sqrt{3}$cm$^3$ |
Cho hình chóp $S.ABCD$ có đáy là hình vuông cạnh $a$, $SA\perp(ABCD)$ và $SA=2a$. Thể tích của khối tứ diện $SBCD$ là
| $\dfrac{a^3}{3}$ | |
| $\dfrac{a^3}{4}$ | |
| $\dfrac{a^3}{6}$ | |
| $\dfrac{a^3}{8}$ |
Cho hình lăng trụ tam giác $ABC.A'B'C'$ có đáy $ABC$ là tam giác đều cạnh $2a$, hình chiếu của $A'$ trên mặt phẳng $(ABC)$ là trung điểm cạnh $BC$. Biết góc giữa hai mặt phẳng $(ABA')$ và $(ABC)$ bằng $45^\circ$. Thể tích khối lăng trụ $ABC.A'B'C'$ bằng
| $\dfrac{3}{2}a^3$ | |
| $\dfrac{1}{2}a^3$ | |
| $2\sqrt{3}a^3$ | |
| $\dfrac{2\sqrt{3}}{3}a^3$ |
Cho khối hộp chữ nhật $ABCD.A'B'C'D'$ có $AB=a$, $AD=\sqrt{2}a$, $AA'=2a$. Thể tích khối hộp đã cho bằng
| $4a^3$ | |
| $2\sqrt{2}a^3$ | |
| $\sqrt{2}a^3$ | |
| $2a^3$ |
Cho hình lăng trụ đứng $ABC.A'B'C'$ có đáy $ABC$ là tam giác vuông tại $B$, $AB=BC=a$ và $AA'=6a$. Thể tích của khối lăng trụ $ABC.A'B'C'$ bằng
| $6a^3$ | |
| $2a^3$ | |
| $3a^3$ | |
| $a^3$ |
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a$, $SA$ vuông góc với mặt phẳng đáy và $SA=9a$. Thể tích khối chóp $S.ABCD$ bằng
| $a^3$ | |
| $27a^3$ | |
| $9a^3$ | |
| $3a^3$ |
Thể tích khối lăng trụ có chiều cao là $h$ và diện tích đáy là $B$ bằng
| $Bh$ | |
| $\dfrac{1}{3}Bh$ | |
| $3Bh$ | |
| $\dfrac{4}{3}Bh$ |
Cho khối hộp chữ nhật $ABCD.A'B'C'D'$. Gọi $M$ là trung điểm của $BB'$. Mặt phẳng $(MDC')$ chia khối hộp chữ nhật thành hai khối đa diện, một khối chứa đỉnh $C$ và một khối chứa đỉnh $A'$. Gọi $V_1,\,V_2$ lần lượt là thể tích hai khối đa diện chứa $C$ và $A'$. Tỉ số $\dfrac{V_1}{V_2}$ bằng
| $\dfrac{V_1}{V_2}=\dfrac{7}{17}$ | |
| $\dfrac{V_1}{V_2}=\dfrac{7}{24}$ | |
| $\dfrac{V_1}{V_2}=\dfrac{17}{24}$ | |
| $\dfrac{V_1}{V_2}=\dfrac{7}{12}$ |
Nếu khối lăng trụ $ABC.A'B'C'$ có thể tích $V$ thì khối chóp $A'.ABC$ có thể tích bằng
| $\dfrac{V}{3}$ | |
| $V$ | |
| $\dfrac{2V}{3}$ | |
| $3V$ |
Cho khối lăng trụ đứng $ABC.A'B'C'$ có đáy $ABC$ là tam giác vuông cân tại $B$, $AB=a$. Biết khoảng cách từ $A$ đến mặt phẳng $(A'BC)$ bằng $\dfrac{\sqrt{6}}{3}a$, thể tích khối lăng trụ đã cho bằng
| $\dfrac{\sqrt{2}}{6}a^3$ | |
| $\dfrac{\sqrt{2}}{2}a^3$ | |
| $\sqrt{2}a^3$ | |
| $\dfrac{\sqrt{2}}{4}a^3$ |
Cho khối lăng trụ có chiều cao $h$ và diện tích đáy $B$. Thể tích khối lăng trụ là
| $V=\dfrac{1}{3}Bh$ | |
| $V=Bh$ | |
| $V=3Bh$ | |
| $V=\dfrac{1}{6}Bh$ |
Cho khối lăng trụ đứng $ABC.A'B'C'$ có đáy là tam giác đều cạnh $a$ và $AA'=2a$ (minh họa như hình vẽ bên).
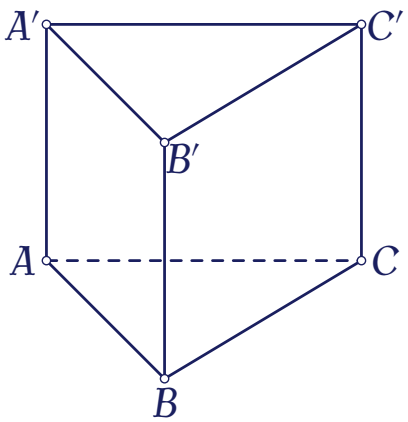
Thể tích của khối lăng trụ đã cho bằng
| $\sqrt{3}a^3$ | |
| $\dfrac{\sqrt{3}a^3}{6}$ | |
| $\dfrac{\sqrt{3}a^3}{3}$ | |
| $\dfrac{\sqrt{3}a^3}{2}$ |
Cho khối lăng trụ đứng $ABC.A'B'C'$ có đáy $ABC$ là tam giác vuông cân tại $A$, $AB=2a$. Góc giữa đường thẳng $BC'$ và mặt phẳng $(ACC'A')$ bằng $30^\circ$. Thể tích của khối lăng trụ đã cho bằng
| $3a^3$ | |
| $a^3$ | |
| $12\sqrt{2}a^3$ | |
| $4\sqrt{2}a^3$ |
Cho khối lăng trụ có diện tích đáy là $3a^2$ và chiều cao $2a$. Thể tích khối lăng trụ đã cho bằng
| $a^3$ | |
| $6a^3$ | |
| $3a^3$ | |
| $2a^3$ |
Cho lăng trụ $ABC.A'B'C'$ có thể tích $V$. Tính thể tích $V_1$ của khối đa diện $BCA'B'C'$ theo $V$.
| $V_1=\dfrac{2}{3}V$ | |
| $V_1=\dfrac{1}{3}V$ | |
| $V_1=\dfrac{1}{2}V$ | |
| $V_1=\dfrac{1}{4}V$ |
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a$. Cạnh bên $SA$ vuông góc với mặt đáy và $SC=a\sqrt{5}$. Tính theo $a$ thể tích $V$ của khối chóp $S.ABCD$.
| $V=\dfrac{a^3\sqrt{3}}{3}$ | |
| $V=\dfrac{a^3\sqrt{3}}{6}$ | |
| $V=a^3\sqrt{3}$ | |
| $V=\dfrac{a^3\sqrt{15}}{3}$ |
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a$ và cạnh bên $SB$ vuông góc với mặt phẳng đáy. Tính chiều cao $h$ của khối chóp, biết rằng thể tích $V=\dfrac{a^3\sqrt{2}}{3}$.
| $h=a\sqrt{2}$ | |
| $h=3a\sqrt{2}$ | |
| $h=a\sqrt{3}$ | |
| $h=\dfrac{a\sqrt{2}}{3}$ |
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông với đường chéo $AC=a\sqrt{2}$, cạnh bên $SB$ vuông góc với mặt phẳng đáy và $SB=a\sqrt{2}$. Tính thể tích $V$ của khối chóp $S.ABCD$.
| $V=\dfrac{a^3\sqrt{2}}{6}$ | |
| $V=\dfrac{a^3\sqrt{2}}{4}$ | |
| $V=a^3\sqrt{2}$ | |
| $V=\dfrac{a^3\sqrt{2}}{3}$ |
