Ba góc của một tam giác vuông tạo thành một cấp số cộng. Hai góc nhọn của tam giác đó có số đo là
| \(20^\circ\) và \(70^\circ\) | |
| \(45^\circ\) và \(45^\circ\) | |
| \(20^\circ\) và \(45^\circ\) | |
| \(30^\circ\) và \(60^\circ\) |
Trong không gian, cho tam giác $ABC$ vuông tại $A$, $AB=2a$, $AC=3a$. Khi quay tam giác $ABC$ quanh cạnh $AB$ thì đường gấp khúc $ACB$ tạo thành một hình nón. Độ dài đường sinh của hình nón đó là
| $a\sqrt{13}$ | |
| $a\sqrt{5}$ | |
| $2a$ | |
| $3a$ |
Cho tam giác $ABC$ vuông tại $A$. Khi quay đường gấp khúc $BCA$ quanh cạnh $AB$ thì tạo thành hình nào dưới đây?
| Hình trụ | |
| Hình cầu | |
| Hình chóp | |
| Hình nón |
Cho khối lăng trụ đứng $ABC.A'B'C'$ có đáy $ABC$ là tam giác vuông cân tại $A$, $AB=2a$. Góc giữa đường thẳng $BC'$ và mặt phẳng $(ACC'A')$ bằng $30^\circ$. Thể tích của khối lăng trụ đã cho bằng
| $3a^3$ | |
| $a^3$ | |
| $12\sqrt{2}a^3$ | |
| $4\sqrt{2}a^3$ |
Cho hàm số $y=x^4-2(m+1)x^2+m^2$ với $m$ là tham số thực. Tìm tất cả các giá trị của $m$ để đồ thị hàm số có $3$ điểm cực trị tạo thành một tam giác vuông.
| $m=-1$ | |
| $m=0$ | |
| $m=1$ | |
| $m>-1$ |
Cho hình chóp $S.ABC$ có đáy là tam giác vuông cân tại $B$, $AB=2a$ và $SA$ vuông góc với mặt phẳng đáy. Khoảng cách từ $C$ đến mặt phẳng $(SAB)$ bằng
| $\sqrt2a$ | |
| $2a$ | |
| $a$ | |
| $2\sqrt2a$ |
Trong không gian $Oxyz$, cho mặt phẳng $(P)\colon4x-3y-1=0$ và hai điểm $A(3;-3;-1)$, $B(9;5;-1)$. Gọi $M$ là điểm thay đổi nằm trên mặt phẳng $(P)$ sao cho tam giác $ABM$ vuông tại $M$. Gọi $S_1,\,S_2$ tương ứng là giá trị nhỏ nhất và giá trị lớn nhất của diện tích tam giác $MAB$. Tính giá trị biểu thức $T=S_2-S_1$.
| $T=5$ | |
| $T=45$ | |
| $T=1$ | |
| $T=10$ |
Tổng ba góc trong tam giác luôn bằng
| $45^\circ$ | |
| $90^\circ$ | |
| $180^\circ$ | |
| $360^\circ$ |
Cho tam giác \(ABC\) vuông tại \(A\) và có \(AB=3\), \(AC=4\). Tính \(\left|\overrightarrow{CA}+\overrightarrow{AB}\right|\).
| \(\left|\overrightarrow{CA}+\overrightarrow{AB}\right|=2\) | |
| \(\left|\overrightarrow{CA}+\overrightarrow{AB}\right|=2\sqrt{13}\) | |
| \(\left|\overrightarrow{CA}+\overrightarrow{AB}\right|=5\) | |
| \(\left|\overrightarrow{CA}+\overrightarrow{AB}\right|=\sqrt{13}\) |
Cho tam giác \(OAB\) vuông tại \(O\) có \(AB=a\) và góc \(\widehat{A}=30^\circ\). Tính diện tích xung quanh của hình nón có được khi quay tam giác \(OAB\) quanh trục \(AO\).
| \(\dfrac{\pi a^2}{4}\) | |
| \(2\pi a^2\) | |
| \(\pi a^2\) | |
| \(\dfrac{\pi a^2}{2}\) |
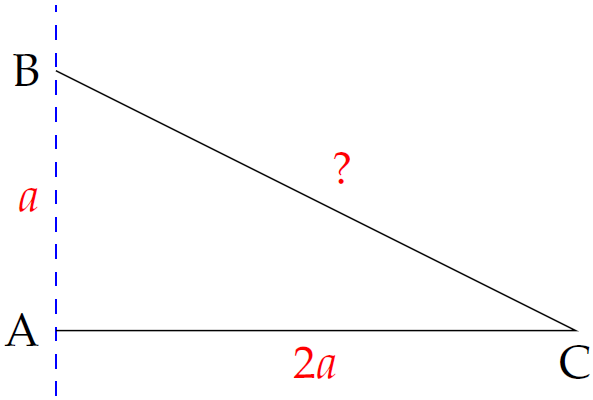
Cho tam giác \(ABC\) vuông tại \(A\) có \(AB=a\), \(AC=2a\). Tính độ dài đường sinh \(\ell\) của hình nón nhận được khi quay tam giác \(ABC\) quanh trục \(AB\).
| \(\ell=a\sqrt{2}\) | |
| \(\ell=2a\) | |
| \(\ell=a\sqrt{3}\) | |
| \(\ell=a\sqrt{5}\) |
Tam giác \(HPS\) có \(\widehat{PHS}=51^\circ\) và \(\widehat{PSH}=15^\circ\) thì \(\widehat{HPS}\) bằng
| \(66^\circ\) | |
| \(144^\circ\) | |
| \(114^\circ\) | |
| \(215^\circ\) |
Cho tam giác \(ABC\) có độ dài ba cạnh là \(a=5\), \(b=7\) và \(c=10\). Phát biểu nào sau đây đúng nhất về số đo ba góc của \(ABC\)?
| \(A>B>C\) | |
| \(B< A< C\) | |
| \(A< B< C\) | |
| \(C< A< B\) |
Tam giác có ba cạnh là \(3\), \(8\), \(9\). Góc lớn nhất có cosin bằng
| \(-\dfrac{1}{6}\) | |
| \(\dfrac{1}{6}\) | |
| \(\dfrac{\sqrt{17}}{4}\) | |
| \(-\dfrac{4}{25}\) |
Cho tam giác \(ABC\) có \(a^2+b^2< c^2\). Khi đó
| Góc \(C\) tù | |
| Góc \(C\) nhọn | |
| Góc \(C\) vuông | |
| Góc \(C\) nhỏ nhất |
Cho tam giác \(ABC\) có \(a^2+b^2-c^2>0\). Khi đó
| Góc \(C\) tù | |
| Góc \(C\) nhọn | |
| Góc \(C\) vuông | |
| Góc \(C\) lớn nhất |
Cho tam giác \(ABC\) thỏa mãn \(b^2+c^2-a^2=\sqrt{3}bc\). Khi đó
| \(\widehat{A}=75^\circ\) | |
| \(\widehat{A}=60^\circ\) | |
| \(\widehat{A}=45^\circ\) | |
| \(\widehat{A}=30^\circ\) |
Trong mặt phẳng \(Oxy\), cho tam giác \(ABC\) biết \(A(1;3)\), \(B(-2;-2)\) và \(C(3;1)\). Tính cosin góc \(A\) của tam giác \(ABC\).
| \(\cos A=\dfrac{2}{\sqrt{17}}\) | |
| \(\cos A=\dfrac{1}{\sqrt{17}}\) | |
| \(\cos A=-\dfrac{2}{\sqrt{17}}\) | |
| \(\cos A=-\dfrac{1}{\sqrt{17}}\) |
Cho tam giác \(ABC\) vuông tại \(A\), có \(\widehat{B}=60^\circ\) và \(AB=a\). Kết quả nào sau đây là sai?
| \(\overrightarrow{AC}\cdot\overrightarrow{CB}=-3a\sqrt{2}\) | |
| \(\overrightarrow{AB}\cdot\overrightarrow{BC}=-a^2\) | |
| \(\overrightarrow{AB}\cdot\overrightarrow{AC}=0\) | |
| \(\overrightarrow{CA}\cdot\overrightarrow{CB}=3a^2\) |
Cho tam giác \(ABC\) có \(AB=9\), \(AC=12\), \(BC=15\). Khi đó, đường trung tuyến \(AM\) của tam giác có độ dài bằng bao nhiêu?
| \(9\) | |
| \(10\) | |
| \(7,5\) | |
| \(8\) |
