Bình Định có câu ca dao:
"Cưới nàng đôi nón Gò Găng
Xấp lãnh An Thái một khăn trầu nguồn."

Nói đến câu ca dao này là nói đến một làng nghề truyền thống có hàng trăm năm tuổi của thị xã An Nhơn, tỉnh Bình Định - làng nghề làm nón lá Gò Găng. Nhân kỷ niệm 10 năm được công nhận thị xã, thị xã An Nhơn lên kế hoạch làm các mô hình biểu tượng làng nghề truyền thống trên địa bàn, trong đó có mô hình chiếc nón lá Gò Găng. Chiếc nón có bán kính đáy \(1\) mét và chiều cao \(1,5\) mét, khung thép dùng làm đường tròn đáy và \(10\) đường nối từ đỉnh của nón đến đường tròn đáy có giá thành \(40.000\) đồng/mét, là của cây lá nón Licuala Fatoua Becc dùng để làm mặt nón có giá thành \(20.000\) đồng/mét vuông. Hỏi nếu bỏ qua diện tích các mép nối thì kinh phí để làm chiếc nón biểu tượng này là bao nhiêu?
| \(1.085.000\) đồng | |
| \(1.086.000\) đồng | |
| \(834.000\) đồng | |
| \(833.000\) đồng |
Cho hình trụ tròn xoay có hai đáy là hai hình tròn $(O,3)$ và $(O',3)$. Biết rằng tồn tại dây cung $AB$ thuộc đường tròn $(O)$ sao cho $\triangle O'AB$ là tam giác đều và mặt phẳng $(O'AB)$ hợp với đáy chứa đường tròn $(O)$ một góc $60^\circ$. Tính diện tích xung quanh $S_{\text{xq}}$ của hình nón có đỉnh $O'$, đáy là hình tròn $(O,3)$.
| $S_{\text{xq}}=\dfrac{54\pi\sqrt{7}}{7}$ | |
| $S_{\text{xq}}=\dfrac{81\pi\sqrt{7}}{7}$ | |
| $S_{\text{xq}}=\dfrac{27\pi\sqrt{7}}{7}$ | |
| $S_{\text{xq}}=\dfrac{36\pi\sqrt{7}}{7}$ |
Cắt hình nón $(X)$ bởi mặt phẳng đi qua đỉnh và tạo với mặt chứa đáy góc $60^\circ$, ta được thiết diện là tam giác đều cạnh $4a$. Diện tích xung quanh của $(X)$ bằng
| $8\sqrt{7}\pi a^2$ | |
| $4\sqrt{13}\pi a^2$ | |
| $8\sqrt{13}\pi a^2$ | |
| $4\sqrt{7}\pi a^2$ |
Diện tích xung quanh của hình nón có độ dài đường sinh \(l\) và bán kính đáy \(r\) bằng
| \(4\pi rl\) | |
| \(2\pi rl\) | |
| \(\pi rl\) | |
| \(\dfrac{1}{3}\pi rl\) |
Cho hình nón có bán kính đáy bằng \(a\) và độ dài đường sinh bằng \(3a\). Diện tích xung quanh của hình nón đó bằng
| \(3\pi a^2\) | |
| \(2\pi a^2\) | |
| \(\pi a^2\) | |
| \(\dfrac{3}{2}\pi a^2\) |
Cho hình nón có bán kính đáy bằng \(a\) và độ dài đường sinh bằng \(2a\). Diện tích xung quanh của hình nón đó bằng
| \(4\pi a^2\) | |
| \(2a^2\) | |
| \(2\pi a^2\) | |
| \(3\pi a^2\) |
Cho hình nón có bán kính đáy \(r=\sqrt{2}\) và độ dài đường sinh \(\ell=3\). Tính diện tích xung quanh của hình nón đã cho.
| \(S_{\text{xq}}=2\pi\) | |
| \(S_{\text{xq}}=3\pi\sqrt{2}\) | |
| \(S_{\text{xq}}=6\pi\) | |
| \(S_{\text{xq}}=6\pi\sqrt{2}\) |
Cho hình nón có thiết diện qua trục là một tam giác đều cạnh bằng \(a\). Tính diện tích mặt xung quanh của hình nón đã cho.
| \(\dfrac{1}{2}\pi a^2\) | |
| \(\pi a^2\) | |
| \(\dfrac{2}{3}\pi a^2\) | |
| \(\dfrac{1}{3}\pi a^2\) |
Tìm bán kính đáy của hình nón có diện tích xung quanh là \(3\pi a^2\) và độ dài đường sinh là \(3a\).
| \(3a\) | |
| \(a\) | |
| \(4a\) | |
| \(2a\) |
Cho hình nón có bán kính đáy bằng \(4a\) và chiều cao bằng \(3a\). Diện tích xung quanh của hình nón bằng
| \(18\pi a^2\) | |
| \(20\pi a^2\) | |
| \(12\pi a^2\) | |
| \(15\pi a^2\) |
Cho hình nón \((N)\) có chiều cao \(h\), bán kính đáy \(R\) và độ dài đường sinh \(\ell\). Công thức tính diện tích xung quanh \(S\) của \((N)\) là
| \(S=\dfrac{1}{3}\pi R\ell\) | |
| \(S=\pi R\ell\) | |
| \(S=4\pi R^2\) | |
| \(S=2\pi R\ell\) |
Cho hình chóp tứ giác đều $S.ABCD$ có cạnh đáy bằng $a$ và chiều cao bằng $2a$, diện tích xung quanh của hình nón đỉnh $S$ và đáy là hình tròn nội tiếp $ABCD$ bằng
| $\dfrac{\pi a^2\sqrt{17}}{8}$ | |
| $\dfrac{\pi a^2\sqrt{15}}{4}$ | |
| $\dfrac{\pi a^2\sqrt{17}}{4}$ | |
| $\dfrac{\pi a^2\sqrt{17}}{6}$ |
Cho hình nón có độ dài đường sinh là $4$ và bán kính là $2$. Diện tích xung quanh hình nón đã cho bằng
| $32\pi$ | |
| $4\pi$ | |
| $16\pi$ | |
| $8\pi$ |
Xét khối nón $(\mathscr{N})$ có đỉnh và đường tròn đáy cùng nằm trên một mặt cầu bán kính bằng 2. Khi $(\mathscr{N})$ có độ dài đường sinh bằng $2\sqrt{3}$, thể tích của nó bằng
| $2\sqrt{3}\pi$ | |
| $3\pi$ | |
| $6\sqrt{3}\pi$ | |
| $\pi$ |
Cho hình nón có đường kính đáy $2r$ và độ dải đường sinh $\ell$. Diện tích xung quanh của hình nón đã cho bằng
| $2\pi r\ell$ | |
| $\dfrac{2}{3}\pi r\ell^2$ | |
| $\pi r\ell$ | |
| $\dfrac{1}{3}\pi r^2\ell$ |
Một bình đựng nước dạng hình nón (không có nắp đậy), đựng đầy nước. Biết rằng chiều cao của bình gấp $3$ lần bán kính đáy của nó. Người ta thả vào bình đó một khối trụ và đo được thể tích nước tràn ra ngoài là $\dfrac{16\pi}{9}\text{dm}^3$. Biết rằng một mặt của khối trụ nằm trên mặt đáy của hình nón và khối trụ có chiều cao bằng đường kính đáy của hình nón (hình vẽ).
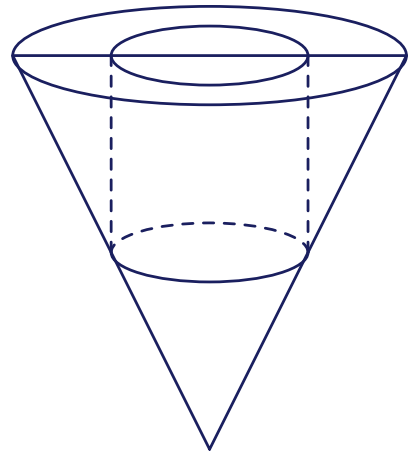
Tính bán kính đáy $R$ của bình nước.
| $R=4$dm | |
| $R=2$dm | |
| $R=3$dm | |
| $R=5$dm |
Cho hình nón có góc ở đỉnh bằng $120^\circ$ và chiều cao bằng $4$. Gọi $(S)$ là mặt cầu đi qua đỉnh và chứa đường tròn đáy của hình nón đã cho. Diện tích của $(S)$ bằng
| $64\pi$ | |
| $256\pi$ | |
| $192\pi$ | |
| $96\pi$ |
Trên bàn có một cốc nước hình trụ chứa đầy nước, có chiều cao bằng $3$ lần đường kính của đáy; một viên bi và một khối nón đều bằng thủy tinh. Biết viên bi là một khối cầu có đường kính bằng đường kính của cốc nước. Người ta từ từ thả vào cốc nước viên bi và khối nón sao cho đỉnh khối nón nằm trên mặt cầu (như hình vẽ) thì thấy nước trong cốc tràn ra ngoài.
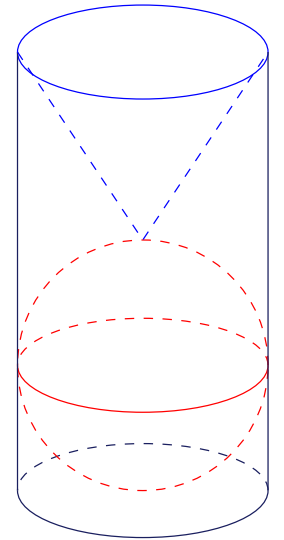
Tính tỉ số thể tích của lượng nước còn lại trong cốc và lượng nước ban đầu (bỏ qua bề dày của lớp vỏ thủy tinh).
| $\dfrac{1}{2}$ | |
| $\dfrac{2}{3}$ | |
| $\dfrac{4}{9}$ | |
| $\dfrac{5}{9}$ |
Thiết diện qua trục của một hình nón tròn xoay là tam giác đều có diện tích bằng $a^2\sqrt{3}$. Tính thể tích $V$ của khối nón đã cho.
| $V=\dfrac{\pi a^3\sqrt{3}}{3}$ | |
| $V=\dfrac{\pi a^3\sqrt{3}}{2}$ | |
| $V=\dfrac{\pi a^3\sqrt{3}}{6}$ | |
| $V=\dfrac{\pi a^3\sqrt{6}}{6}$ |
Diện tích xung quanh của hình nón có độ dài đường sinh $\ell$ và bán kính đáy $r$ bằng
| $\pi r\left(\ell+r\right)$ | |
| $\pi r\ell$ | |
| $2\pi r\ell$ | |
| $\dfrac{1}{3}\pi r\ell$ |
