Cho tam giác \(ABC\). Biểu thức nào dưới đây dùng để tính \(\cos C\)?

	\(\dfrac{b^2+c^2-a^2}{2bc}\)
	\(\dfrac{a^2+c^2-b^2}{2ac}\)
	\(\dfrac{a^2+b^2-c^2}{2ab}\)
	\(\dfrac{c}{2R}\)

Cho tam giác \(ABC\) có \(b=7\), \(c=5\), \(\cos A=\dfrac{3}{5}\). Đường cao \(h_a\) của tam giác \(ABC\) là

	\(8\)
	\(\dfrac{7\sqrt{2}}{2}\)
	\(80\sqrt{3}\)
	\(8\sqrt{3}\)

Tam giác \(ABC\) có \(AB=5\) cm, \(AC=8\) cm và góc \(\widehat{A}=60^\circ\). Độ dài cạnh \(BC\) bằng

	\(7\) cm
	\(49\) cm
	\(11,4\) cm
	\(4,44\) cm

Cho \(\triangle ABC\) có ba cạnh lần lượt là \(a,\,b,\,c\). Công thức tính diện tích \(\triangle ABC\) là

	\(S=\dfrac{a\cdot b\cdot c}{2R}\)
	\(S=p\cdot R\)
	\(S=\dfrac{1}{2}a\cdot b\cdot\cos C\)
	\(S=\dfrac{1}{2}a\cdot c\cdot\sin B\)

Cho tam giác \(ABC\). Kết quả nào sau đây không đúng?

	\(S=\dfrac{abc}{2R}\)
	\(S=\dfrac{1}{2}ac\sin B\)
	\(S=\dfrac{a+b+c}{2}r\)
	\(S=\sqrt{p(p-a)(p-b)(p-c)}\)

Tam giác có ba cạnh là \(3\), \(8\), \(9\). Góc lớn nhất có cosin bằng

	\(-\dfrac{1}{6}\)
	\(\dfrac{1}{6}\)
	\(\dfrac{\sqrt{17}}{4}\)
	\(-\dfrac{4}{25}\)

Cho tam giác \(ABC\) thỏa mãn \(b+c=2a\). Mệnh đề nào dưới đây là đúng?

	\(\cos B+\cos C=2\cos A\)
	\(\sin B+\sin C=2\sin A\)
	\(\sin B+\sin C=2\cos A\)
	\(\sin B+\cos C=2\sin A\)

Tam giác \(ABC\) có \(a=2\), \(b=\sqrt{6}\), \(c=1+\sqrt{3}\). Góc \(\widehat{B}\) bằng

	\(115^\circ\)
	\(75^\circ\)
	\(60^\circ\)
	\(53^\circ32'\)

Tam giác \(ABC\) có \(a=8\), \(c=3\), \(\widehat{B}=60^\circ\). Độ dài cạnh \(b\) bằng bao nhiêu?

	\(49\)
	\(\sqrt{97}\)
	\(7\)
	\(\sqrt{61}\)

Tam giác \(ABC\) có ba cạnh \(a=5\), \(b=3\), \(c=5\). Số đo góc \(\widehat{BAC}\) là

	\(\widehat{A}>60^\circ\)
	\(\widehat{A}=30^\circ\)
	\(\widehat{A}=45^\circ\)
	\(\widehat{A}=90^\circ\)

Trong tam giác \(ABC\) có \(AB=2\)cm, \(AC=1\)cm, \(\widehat{A}=60^\circ\). Khi đó độ dài cạnh \(BC\) là

	\(1\)cm
	\(2\)cm
	\(\sqrt{3}\)cm
	\(\sqrt{5}\)cm

Cho tam giác \(ABC\) có \(a=2\), \(b=\sqrt{6}\), \(c=1+\sqrt{3}\). Góc \(A\) có số đo bằng

	\(30^\circ\)
	\(45^\circ\)
	\(68^\circ\)
	\(75^\circ\)

Cho \(\triangle ABC\) có các cạnh \(BC=a\), \(AC=b\), \(AB=c\). Diện tích của \(\triangle ABC\) là

	\(S=\dfrac{1}{2}ac\sin C\)
	\(S=\dfrac{1}{2}bc\sin B\)
	\(S=\dfrac{1}{2}ac\sin B\)
	\(S=\dfrac{1}{2}bc\sin C\)

Tam giác $HPS$ đều, cạnh $PS=a\sqrt{2}$. $S_{HPS}$ bằng

	$a^2\dfrac{\sqrt{3}}{4}$
	$a^2\dfrac{\sqrt{6}}{4}$
	$a^2\dfrac{\sqrt{3}}{2}$
	$a^2\dfrac{\sqrt{6}}{2}$

Tam giác $ABC$ có độ dài ba cạnh lần lượt là $21$cm, $17$cm và $10$cm. Tính diện tích tam giác.

	$S=16\text{ cm}^2$
	$S=24\text{ cm}^2$
	$S=48\text{ cm}^2$
	$S=84\text{ cm}^2$

Tam giác $ABC$ vuông cân tại $B$, có cạnh $AB=2a$. Phát biểu nào sau đây không đúng?

	$S=\dfrac{a^2}{2}$
	$\widehat{A}=\widehat{C}=45^\circ$
	$AB=BC=2a$
	$S=2a^2$

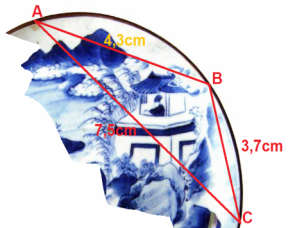
Trong khi khai quật một ngôi mộ cổ, các nhà khảo cổ học đã tìm được một chiếc đĩa cổ hình tròn bị vỡ, các nhà khảo cổ muốn khôi phục lại hình dạng chiếc đĩa này. Để xác định bán kính của chiếc đĩa, các nhà khảo cổ lấy \(3\) điểm trên chiếc đĩa và tiến hành đo đạc thu được kết quả như hình vẽ (\(AB=4,3\) cm; \(BC=3,7\) cm; \(CA=7,5\) cm). Bán kính của chiếc đĩa này bằng

	\(6,01\)
	\(5,73\)
	\(5,85\)
	\(4,57\)

Tam giác \(ABC\) có \(AB=8\)cm, \(AC=18\)cm và diện tích bằng \(64\)cm\(^2\). Giá trị \(\sin A\) là

	\(\dfrac{\sqrt{3}}{2}\)
	\(\dfrac{3}{8}\)
	\(\dfrac{4}{5}\)
	\(\dfrac{8}{9}\)

Cho tam giác \(ABC\) có độ dài ba cạnh là \(a=5\), \(b=7\) và \(c=10\). Phát biểu nào sau đây đúng nhất về số đo ba góc của \(ABC\)?

	\(A>B>C\)
	\(B< A< C\)
	\(A< B< C\)
	\(C< A< B\)

Gọi \(R\) là bán kính đường tròn ngoại tiếp tam giác \(ABC\). Khẳng định nào sau đây sai?

	\(\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}=2R\)
	\(a=2R\sin A\)
	\(a=c\dfrac{\sin A}{\sin C}\)
	\(\dfrac{a}{b}=\dfrac{\sin B}{\sin A}\)