Cho tam giác \(ABC\) có \(AB=9\), \(AC=12\), \(BC=15\). Khi đó, đường trung tuyến \(AM\) của tam giác có độ dài bằng bao nhiêu?
| \(9\) | |
| \(10\) | |
| \(7,5\) | |
| \(8\) |
Tam giác \(ABC\) vuông cân tại \(A\) có \(AB=a\). Đường tròn nội tiếp tam giác \(ABC\) có bán kính \(r\) bằng
| \(\dfrac{a}{2}\) | |
| \(\dfrac{a}{\sqrt{2}}\) | |
| \(\dfrac{a}{2+\sqrt{2}}\) | |
| \(\dfrac{a}{3}\) |
Cho tam giác \(ABC\) có độ dài ba cạnh là \(AB=2\), \(BC=5\), \(CA=6\). Tính độ dài đường trung tuyến \(AM\).
| \(\dfrac{\sqrt{15}}{2}\) | |
| \(\dfrac{\sqrt{55}}{2}\) | |
| \(\dfrac{\sqrt{110}}{2}\) | |
| \(\sqrt{55}\) |
Tam giác \(ABC\) có \(a=2\sqrt{2}\), \(b=2\sqrt{3}\), \(c=2\). Độ dài trung tuyến \(m_b\) bằng
| \(\sqrt{3}\) | |
| \(5\) | |
| \(3\) | |
| \(2\) |
Cho tam giác \(ABC\) với \(a,\,b,\,c\) lần lượt là độ dài các cạnh \(BC\), \(CA\), \(AB\). Chọn mệnh đề sai trong các mệnh đề sau:
| \(a^2=b^2+c^2-2bc\cos A\) | |
| \(m_a^2=\dfrac{b^2+c^2}{2}-\dfrac{a^2}{4}\) | |
| \(S=\dfrac{1}{2}ab\cos C\) | |
| \(\cos A=\dfrac{b^2+c^2-a^2}{2bc}\) |
Tam giác \(ABC\) có \(AB=8\)cm, \(BC=10\)cm, \(CA=6\)cm. Đường trung tuyến \(AM\) của tam giác đó có độ dài bằng
| \(4\)cm | |
| \(5\)cm | |
| \(6\)cm | |
| \(7\)cm |
Trong không gian $Oxyz$, cho hai điểm $M(1;2;3)$, $A(2;4;4)$ và hai mặt phẳng $(P)\colon x+y-2z+1=0$, $(Q)\colon x-2y-z+4=0$. Viết phương trình đường thẳng $\Delta$ đi qua $M$, cắt $(P)$, $(Q)$ lần lượt tại $B,\,C$ sao cho tam giác $ABC$ cân tại $A$ và nhận $AM$ làm đường trung tuyến.
| $\dfrac{x-1}{-1}=\dfrac{y-2}{-1}=\dfrac{z-3}{1}$ | |
| $\dfrac{x-1}{1}=\dfrac{y-2}{-1}=\dfrac{z-3}{1}$ | |
| $\dfrac{x-1}{1}=\dfrac{y-2}{-1}=\dfrac{z-3}{-1}$ | |
| $\dfrac{x-1}{2}=\dfrac{y-2}{-1}=\dfrac{z-3}{1}$ |
Trong không gian $Oxyz$, cho tam giác $ABC$ với $A(1;-3;4)$, $B(-2;-5;-7)$, $C(6;-3;-1)$. Viết phương trình đường trung tuyến $AM$ của tam giác $ABC$.
Cho khối lăng trụ đứng $ABC.A'B'C'$ có đáy $ABC$ là tam giác vuông cân tại $A$, $AB=2a$. Góc giữa đường thẳng $BC'$ và mặt phẳng $(ACC'A')$ bằng $30^\circ$. Thể tích của khối lăng trụ đã cho bằng
| $3a^3$ | |
| $a^3$ | |
| $12\sqrt{2}a^3$ | |
| $4\sqrt{2}a^3$ |
Tính thể tích $V$ của vật thể giới hạn bởi hai mặt phẳng $x=0,\,x=\pi$. Biết rằng thiết diện của vật thể cắt bởi mặt phẳng vuông góc với $Ox$ tại điểm có hoành độ $x\,(0\leq x\leq\pi)$ là một tam giác vuông cân có cạnh huyền bằng $\sin x+2$.
| $\dfrac{7\pi}{6}+1$ | |
| $\dfrac{9\pi}{8}+1$ | |
| $\dfrac{7\pi}{6}+2$ | |
| $\dfrac{9\pi}{8}+2$ |
Cho hình lăng trụ đứng $ABC.A'B'C'$ có đáy $ABC$ là tam giác vuông cân tại $B$ và $AB=4$ (tham khảo hình bên).
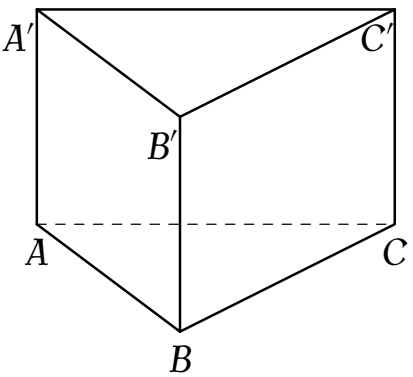
Khoảng cách từ $C$ đến mặt phẳng $\left(ABB'A'\right)$ bằng
| $2\sqrt{2}$ | |
| $2$ | |
| $\sqrt{2}$ | |
| $4$ |
- Giả sử hai hàm số $y=f\left(x\right)$ và $y=f\left(x+1\right)$ đều liên tục trên đoạn $\left[0;2\right]$ và $f\left(0\right)=f\left(2\right)$. Chứng minh phương trình $f\left(x\right)-f\left(x+1\right)=0$ luôn có nghiệm thuộc đoạn $\left[0;1\right]$.
- Cho hàm số $y=\dfrac{x+2}{x+1}$ có đồ thị $\left(\mathscr{C}\right)$. Tìm điểm $M$ thuộc $\left(\mathscr{C}\right)$ sao cho tiếp tuyến của $\left(\mathscr{C}\right)$ tại $M$ tạo với hai trục tọa độ một tam giác vuông cân.
Cho tam giác $ABC$ có độ dài ba cạnh lần lượt là $3$, $5$, $6$. Tính bán kính đường tròn nội tiếp của $ABC$.
| $r=\dfrac{\sqrt{14}}{7}$ | |
| $r=\dfrac{2\sqrt{14}}{7}$ | |
| $r=2\sqrt{14}$ | |
| $r=\dfrac{6\sqrt{77}}{7}$ |
Tam giác $HPS$ đều, cạnh $PS=a\sqrt{2}$. $S_{HPS}$ bằng
| $a^2\dfrac{\sqrt{3}}{4}$ | |
| $a^2\dfrac{\sqrt{6}}{4}$ | |
| $a^2\dfrac{\sqrt{3}}{2}$ | |
| $a^2\dfrac{\sqrt{6}}{2}$ |
Tam giác $ABC$ có độ dài ba cạnh lần lượt là $21$cm, $17$cm và $10$cm. Tính bán kính đường tròn ngoại tiếp.
| $R=\dfrac{85}{8}$cm | |
| $R=\dfrac{85}{2}$cm | |
| $R=\dfrac{7}{4}$cm | |
| $R=\dfrac{7}{2}$cm |
Tam giác $ABC$ có độ dài ba cạnh lần lượt là $21$cm, $17$cm và $10$cm. Tính diện tích tam giác.
| $S=16\text{ cm}^2$ | |
| $S=24\text{ cm}^2$ | |
| $S=48\text{ cm}^2$ | |
| $S=84\text{ cm}^2$ |
Tam giác $ABC$ vuông cân tại $B$, có cạnh $AB=2a$. Phát biểu nào sau đây không đúng?
| $S=\dfrac{a^2}{2}$ | |
| $\widehat{A}=\widehat{C}=45^\circ$ | |
| $AB=BC=2a$ | |
| $S=2a^2$ |
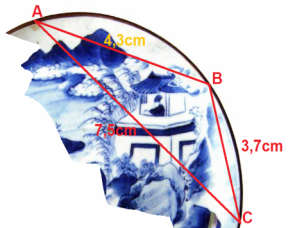
Trong khi khai quật một ngôi mộ cổ, các nhà khảo cổ học đã tìm được một chiếc đĩa cổ hình tròn bị vỡ, các nhà khảo cổ muốn khôi phục lại hình dạng chiếc đĩa này. Để xác định bán kính của chiếc đĩa, các nhà khảo cổ lấy \(3\) điểm trên chiếc đĩa và tiến hành đo đạc thu được kết quả như hình vẽ (\(AB=4,3\) cm; \(BC=3,7\) cm; \(CA=7,5\) cm). Bán kính của chiếc đĩa này bằng
| \(6,01\) | |
| \(5,73\) | |
| \(5,85\) | |
| \(4,57\) |
Tam giác \(ABC\) có \(AB=5\) cm, \(AC=8\) cm và góc \(\widehat{A}=60^\circ\). Độ dài cạnh \(BC\) bằng
| \(7\) cm | |
| \(49\) cm | |
| \(11,4\) cm | |
| \(4,44\) cm |
Cho \(\triangle ABC\) có ba cạnh lần lượt là \(a,\,b,\,c\). Công thức tính diện tích \(\triangle ABC\) là
| \(S=\dfrac{a\cdot b\cdot c}{2R}\) | |
| \(S=p\cdot R\) | |
| \(S=\dfrac{1}{2}a\cdot b\cdot\cos C\) | |
| \(S=\dfrac{1}{2}a\cdot c\cdot\sin B\) |
