Trong mặt phẳng \(Oxy\), cho ba điểm \(A(-1;5)\), \(B(5;5)\), \(C(-1;11)\). Khẳng định nào sau đây đúng?
| \(A,\,B,\,C\) thẳng hàng | |
| \(\overrightarrow{AB},\,\overrightarrow{AC}\) cùng phương | |
| \(\overrightarrow{AB},\,\overrightarrow{AC}\) không cùng phương | |
| \(\overrightarrow{AB},\,\overrightarrow{AC}\) cùng hướng |
Trong mặt phẳng \(Oxy\), cho bốn điểm \(A(3;-2)\), \(B(7;1)\), \(C(0;1)\), \(D(-8;-5)\). Khẳng định nào sau đây đúng?
| \(\overrightarrow{AB},\,\overrightarrow{CD}\) đối nhau | |
| \(\overrightarrow{AB},\,\overrightarrow{CD}\) ngược hướng | |
| \(\overrightarrow{AB},\,\overrightarrow{CD}\) cùng hướng | |
| \(A,\,B,\,C,\,D\) thẳng hàng |
Trong không gian \(Oxyz\), cho hai vectơ \(\vec{a},\,\vec{b}\neq\vec{0}\). Đặt \(\vec{c}=\left[\vec{a},\vec{b}\right]\), mệnh đề nào sau đây là đúng?
| \(\vec{a},\,\vec{c}\) cùng phương | |
| \(\vec{b},\,\vec{c}\) cùng phương | |
| \(\vec{c}\) vuông góc với cả \(\vec{a}\) và \(\vec{b}\) | |
| \(\vec{a},\,\vec{b},\,\vec{c}\) đồng phẳng |
Cho tam giác \(ABC\) và điểm \(M\) thỏa mãn \(\overrightarrow{MA}=\overrightarrow{MB}+\overrightarrow{MC}\). Khẳng định nào sau đây đúng?
| \(A,\,B,\,C\) thẳng hàng | |
| \(AM\) là phân giác trong của góc \(\widehat{BAC}\) | |
| \(A,\,M\) và trọng tâm tam giác \(ABC\) thẳng hàng | |
| \(\overrightarrow{AM}+\overrightarrow{BC}=\vec{0}\) |
Cho \(\vec{a}\) và \(\vec{b}\) (khác \(\vec{0}\)) là các vectơ đối nhau. Khẳng định nào sau đây sai?
| \(\vec{a},\,\vec{b}\) cùng phương | |
| \(\vec{a},\,\vec{b}\) ngược hướng | |
| \(\vec{a},\,\vec{b}\) cùng độ dài | |
| \(\vec{a},\,\vec{b}\) cùng hướng |
Hai vectơ có cùng độ dài và ngược hướng gọi là
| Hai vectơ cùng hướng | |
| Hai vectơ cùng phương | |
| Hai vectơ bằng nhau | |
| Hai vectơ đối nhau |
Cho ba điểm \(M,\,N,\,P\) thẳng hàng, trong đó điểm \(N\) nằm giữa \(M\) và \(P\). Khi đó các cặp vectơ nào sau đây cùng hướng?
| \(\overrightarrow{MP}\) và \(\overrightarrow{PN}\) | |
| \(\overrightarrow{MN}\) và \(\overrightarrow{PN}\) | |
| \(\overrightarrow{NM}\) và \(\overrightarrow{NP}\) | |
| \(\overrightarrow{MN}\) và \(\overrightarrow{MP}\) |
Cho lục giác đều \(ABCDEF\) có tâm \(O\).
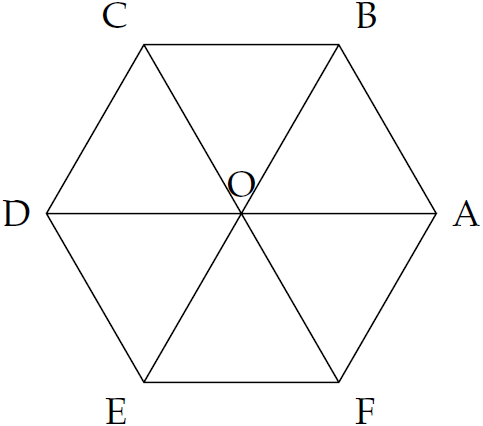
Có bao nhiêu vectơ (khác \(\vec{0}\)) ngược hướng với vectơ \(\overrightarrow{OB}\) mà có điểm đầu và điểm cuối là một trong các đỉnh và tâm của \(ABCDEF\)?
| \(3\) | |
| \(9\) | |
| \(5\) | |
| \(4\) |
Chọn mệnh đề đúng trong các mệnh đề sau?
| Hai vectơ có giá song song thì cùng phương | |
| Hai vectơ không cùng phương thì ngược hướng | |
| Hai vectơ không cùng phương thì cắt nhau | |
| Hai vectơ có cùng độ dài thì bằng nhau |
Mệnh đề nào dưới đây đúng?
| Hai vectơ (khác \(\vec{0}\)) bằng nhau thì không bao giờ cùng phương | |
| Hai vectơ bằng nhau thì chúng phải có điểm đầu và điểm cuối trùng nhau | |
| Hai vectơ (khác \(\vec{0}\)) cùng phương thì song song | |
| Hai vectơ bằng nhau thì cùng hướng |
Khẳng định nào sau đây đúng?
| Hai vectơ cùng phương với một vectơ thứ ba thì cùng phương | |
| Hai vectơ cùng phương với một vectơ thứ ba khác \(\vec{0}\) thì cùng phương | |
| Hai vectơ ngược hướng với một vectơ thứ ba thì ngược hướng | |
| Hai vectơ bằng nhau khi và chỉ khi chúng có độ dài bằng nhau |
Phát biểu nào sau đây là sai?
| Hai vectơ cùng hướng thì cùng phương | |
| Hai vectơ ngược hướng thì cùng phương | |
| Hai vectơ ngược hướng thì không cùng phương | |
| Độ dài của vectơ là khoảng cách giữa điểm đầu và điểm cuối |
Phát biểu nào sau đây là sai?
| Vectơ là đoạn thẳng có hướng | |
| Hai vectơ cùng hướng thì cùng phương | |
| Vectơ \(\vec{0}\) cùng phương với mọi vectơ | |
| Hai vectơ cùng phương thì cùng hướng |
Mệnh đề nào sau đây đúng?
| Có duy nhất một vectơ cùng phương với mọi vectơ | |
| Có ít nhất hai vectơ có cùng phương với mọi vectơ | |
| Có vô số vectơ cùng phương với mọi vectơ | |
| Không có vectơ nào cùng phương với mọi vectơ |
Trong không gian $Oxyz$, cho các vectơ $\overrightarrow{a}=(2;m-1;3)$, $\overrightarrow{b}=(1;3;-2n)$. Tìm $m,\,n$ để các vectơ $\overrightarrow{a},\,\overrightarrow{b}$ cùng phương.
| $m=7$; $n=\dfrac{3}{4}$ | |
| $m=1$; $n=0$ | |
| $m=4$; $n=-3$ | |
| $m=7$; $n=-\dfrac{3}{4}$ |
Trong không gian $Oxyz$, cho vectơ $\overrightarrow{a}=-3\overrightarrow{j}+4\overrightarrow{k}$. Tọa độ của vectơ $\overrightarrow{a}$ là
| $(0;-4;3)$ | |
| $(-3;0;4)$ | |
| $(0;3;4)$ | |
| $(0;-3;4)$ |
Trong không gian $Oxyz$, các véctơ đơn vị trên các trục $Ox$, $Oy$, $Oz$ lần lượt là $\overrightarrow{i}$, $\overrightarrow{j}$, $\overrightarrow{k}$, cho điểm $M\left(2;-1; 1\right)$. Khẳng định nào sau đây là đúng?
| $\overrightarrow{OM}=\overrightarrow{k}+\overrightarrow{j}+2\overrightarrow{i}$ | |
| $\overrightarrow{OM}=2\overrightarrow{k}-\overrightarrow{j}+\overrightarrow{i}$ | |
| $\overrightarrow{OM}=2\overrightarrow{i}-\overrightarrow{j}+\overrightarrow{k}$ | |
| $\overrightarrow{OM}=\overrightarrow{i}+\overrightarrow{j}+2\overrightarrow{k}$ |
Trong không gian cho hai vectơ $\overrightarrow{u}$, $\overrightarrow{v}$ tạo với nhau một góc $60^\circ$, $\left|\overrightarrow{u}\right|=2$ và $\left|\overrightarrow{v}\right|=3$. Tích vô hướng $\overrightarrow{u}\cdot\overrightarrow{v}$ bằng
| $3$ | |
| $6$ | |
| $2$ | |
| $3\sqrt{3}$ |
Trong không gian, với $\overrightarrow{a}$, $\overrightarrow{b}$, $\overrightarrow{c}$ là ba vectơ bất kỳ, mệnh đề nào dưới đây đúng?
| $\overrightarrow{a}\left(\overrightarrow{b}+\overrightarrow{c}\right)=\overrightarrow{a}\cdot\overrightarrow{b}+\overrightarrow{a}\cdot \overrightarrow{c}$ | |
| $\overrightarrow{a}\left(\overrightarrow{b}-\overrightarrow{c}\right)=\overrightarrow{a}\cdot \overrightarrow{b}+\overrightarrow{a}\cdot \overrightarrow{c}$ | |
| $\overrightarrow{a}\left(\overrightarrow{b}+\overrightarrow{c}\right)=\overrightarrow{a}\cdot \overrightarrow{b}-\overrightarrow{a}\cdot \overrightarrow{c}$ | |
| $\overrightarrow{a}\left(\overrightarrow{b}+\overrightarrow{c}\right)=\overrightarrow{a}\cdot \overrightarrow{b}+\overrightarrow{b}\cdot \overrightarrow{c}$ |
Trong không gian, cho hình bình hành $ABCD$. Vectơ $\overrightarrow{AB}+\overrightarrow{AD}$ bằng
| $\overrightarrow{AC}$ | |
| $\overrightarrow{BC}$ | |
| $\overrightarrow{BD}$ | |
| $\overrightarrow{CA}$ |
