Trong mặt phẳng \(Oxy\), cho bốn điểm \(A(1;1)\), \(B(2;-1)\), \(C(4;3)\), \(D(3;5)\). Khẳng định nào sau đây đúng?

	Tứ giác \(ABCD\) là hình bình hành
	\(G(9;7)\) là trọng tâm tam giác \(BCD\)
	\(\overrightarrow{AB}=\overrightarrow{CD}\)
	\(\overrightarrow{AC},\,\overrightarrow{AD}\) cùng phương

Cho tam giác \(ABC\) có \(M\) là điểm thỏa mãn \(\overrightarrow{MA}-\overrightarrow{MB}+\overrightarrow{MC}=\vec{0}\). Mệnh đề nào sau đây sai?

	\(MABC\) là hình bình hành
	\(\overrightarrow{AM}+\overrightarrow{AB}=\overrightarrow{AC}\)
	\(\overrightarrow{BA}+\overrightarrow{BC}=\overrightarrow{BM}\)
	\(\overrightarrow{MA}=\overrightarrow{BC}\)

Cho hình bình hành \(ABCD\), có \(I\) là giao điểm của hai đường chéo. Khẳng định nào sau đây là sai?

	\(\overrightarrow{IA}+\overrightarrow{IC}=\overrightarrow{0}\)
	\(\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}\)
	\(\overrightarrow{AB}=\overrightarrow{DC}\)
	\(\overrightarrow{AC}=\overrightarrow{BD}\)

Cho hai hình bình hành \(ABCD\) và \(ABEF\) có chung cạnh \(AB\).

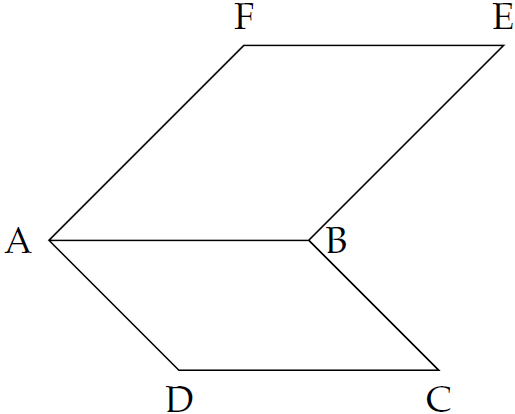
Vectơ nào sau đây bằng với vectơ \(\overrightarrow{CE}\)?

	\(\overrightarrow{AF}\)
	\(\overrightarrow{DF}\)
	\(\overrightarrow{BF}\)
	\(\overrightarrow{BD}\)

Cho hình bình hành \(ABCD\). Đẳng thức nào sau đây đúng?

	\(\overrightarrow{DA}=\overrightarrow{BC}\)
	\(\overrightarrow{AC}=\overrightarrow{BD}\)
	\(\overrightarrow{BA}=\overrightarrow{CD}\)
	\(\overrightarrow{BA}=\overrightarrow{DC}\)

Cho hình bình hành \(ABCD\), tâm \(O\). Đẳng thức nào sau đây sai?

	\(\overrightarrow{BA}=\overrightarrow{CD}\)
	\(\left|\overrightarrow{AB}\right|=\left|\overrightarrow{CD}\right|\)
	\(\overrightarrow{OA}=\overrightarrow{OC}\)
	\(\overrightarrow{AO}=\overrightarrow{OC}\)

Cho tứ giác \(ABCD\). Gọi \(M,\,N,\,P,\,Q\) lần lượt là trung điểm của \(AB\), \(BC\), \(CD\), \(DA\). Khẳng định nào sau đây sai?

	\(\overrightarrow{MN}=\overrightarrow{QP}\)
	\(\left|\overrightarrow{QP}\right|=\left|\overrightarrow{MN}\right|\)
	\(\overrightarrow{MQ}=\overrightarrow{NP}\)
	\(\left|\overrightarrow{MN}\right|=\left|\overrightarrow{AC}\right|\)

Cho hình bình hành \(ABCD\) tâm \(O\). Đẳng thức nào sau đây sai?

	\(\overrightarrow{AB}=\overrightarrow{DC}\)
	\(\overrightarrow{OB}=\overrightarrow{DO}\)
	\(\overrightarrow{OA}=\overrightarrow{OC}\)
	\(\overrightarrow{CB}=\overrightarrow{DA}\)

Cho bốn điểm phân biệt \(A,\,B,\,C,\,D\) thỏa mãn \(\overrightarrow{AB}=\overrightarrow{CD}\). Khẳng định nào sau đây sai?

	\(\overrightarrow{AB}\) cùng hướng với \(\overrightarrow{CD}\)
	\(\overrightarrow{AB}\) cùng phương với \(\overrightarrow{CD}\)
	\(\left|\overrightarrow{AB}\right|=\left|\overrightarrow{CD}\right|\)
	\(ABCD\) là hình bình hành

Cho bốn điểm phân biệt \(A,\,B,\,C,\,D\) mà trong đó không có ba điểm nào thẳng hàng. Điều kiện cần và đủ để \(\overrightarrow{AB}=\overrightarrow{CD}\) là

	\(ABCD\) là hình bình hành
	\(ABDC\) là hình bình hành
	\(AC=BD\)
	\(AB=CD\)

Cho hình bình hành $ABCD$. Phép tịnh tiến theo vectơ nào sau đây biến đường thẳng $AB$ thành đường thẳng $CD$ và biến đường thẳng $AD$ thành đường thẳng $BC$?

	$\overrightarrow{AC}$
	$\overrightarrow{CA}$
	$\overrightarrow{BD}$
	$\overrightarrow{DB}$

Trong không gian, cho hình bình hành $ABCD$. Vectơ $\overrightarrow{AB}+\overrightarrow{AD}$ bằng

	$\overrightarrow{AC}$
	$\overrightarrow{BC}$
	$\overrightarrow{BD}$
	$\overrightarrow{CA}$

Trong không gian \(Oxyz\), cho hai vectơ \(\overrightarrow{u}=(1;2;3)\) và \(\overrightarrow{v}=(-5;1;1)\). Khẳng định nào đúng?

	\(\left|\overrightarrow{u}\right|=\left|\overrightarrow{v}\right|\)
	\(\overrightarrow{u}=\overrightarrow{v}\)
	\(\overrightarrow{u}\bot\overrightarrow{v}\)
	\(\overrightarrow{u}\) cùng phương với \(\overrightarrow{v}\)

Trong không gian \(Oxyz\), cho \(A(1;-1;0)\), \(B(0;2;0)\) và \(C(2;1;3)\). Tọa độ điểm \(M\) thỏa mãn \(\overrightarrow{MA}-\overrightarrow{MB}+\overrightarrow{MC}=\vec{0}\) là

	\(M(3;2;-3)\)
	\(M(3;-2;3)\)
	\(M(3;-2;-3)\)
	\(M(3;2;3)\)

Trong không gian \(Oxyz\), cho ba vectơ \(\vec{a}=(3;-1;-2)\), \(\vec{b}=(1;2;m)\) và \(\vec{c}=(5;1;7)\). Tìm giá trị của \(m\) để \(\left[\vec{a},\vec{b}\right]=\vec{c}\).

	\(m=-1\)
	\(m=0\)
	\(m=1\)
	\(m=2\)

Gọi \(M\) là trung điểm của đoạn thẳng \(AB\). Khẳng định nào sau đây là sai?

	\(\overrightarrow{AB}=2\overrightarrow{MB}\)
	\(\overrightarrow{MA}+\overrightarrow{MB}=\vec{0}\)
	\(\overrightarrow{MA}=-\dfrac{1}{2}\overrightarrow{AB}\)
	\(\overrightarrow{MA}=\overrightarrow{MB}\)

Cho hình bình hành \(ABCD\), tâm \(M\). Mệnh đề nào sau đây sai?

	\(\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}\)
	\(\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}\)
	\(\overrightarrow{BA}+\overrightarrow{BC}=2\overrightarrow{BM}\)
	\(\overrightarrow{MA}+\overrightarrow{MB}=\overrightarrow{MC}+\overrightarrow{MD}\)

Cho hình bình hành \(ABCD\). Đẳng thức nào sau đây đúng?

	\(\overrightarrow{AC}+\overrightarrow{BD}=2\overrightarrow{BC}\)
	\(\overrightarrow{AC}+\overrightarrow{BD}=\overrightarrow{AB}\)
	\(\overrightarrow{AC}-\overrightarrow{BD}=2\overrightarrow{CD}\)
	\(\overrightarrow{AC}-\overrightarrow{AD}=\overrightarrow{CD}\)

Cho tam giác \(ABC\). Gọi \(M,\,N\) lần lượt là trung điểm của \(AB\) và \(AC\). Khẳng định nào sau đây sai?

	\(\overrightarrow{AB}=2\overrightarrow{AM}\)
	\(\overrightarrow{AC}=2\overrightarrow{NC}\)
	\(\overrightarrow{CB}=-2\overrightarrow{MN}\)
	\(\overrightarrow{CN}=-\dfrac{1}{2}\overrightarrow{AC}\)

Cho tam giác \(ABC\) cân tại \(A\), đường cao \(AH\). Khẳng định nào sau đây sai?

	\(\overrightarrow{AB}=\overrightarrow{AC}\)
	\(\overrightarrow{HC}=-\overrightarrow{HB}\)
	\(\left|\overrightarrow{AB}\right|=\left|\overrightarrow{AC}\right|\)
	\(\overrightarrow{BC}=2\overrightarrow{HC}\)