Ngân hàng bài tập
A
Tam giác \(ABC\) với \(a=2\), \(b=\sqrt{6}\), \(c=1+\sqrt{3}\) có bán kính đường tròn ngoại tiếp bằng
| \(R=\dfrac{\sqrt{2}}{3}\) | |
| \(R=\dfrac{\sqrt{2}}{2}\) | |
| \(R=\sqrt{2}\) | |
| \(R=\sqrt{3}\) |
2 lời giải
Chọn phương án C.
Tìm bán kính đường tròn ngoại tiếp thông qua việc tính diện tích tam giác.
- Tính nửa chu vi:
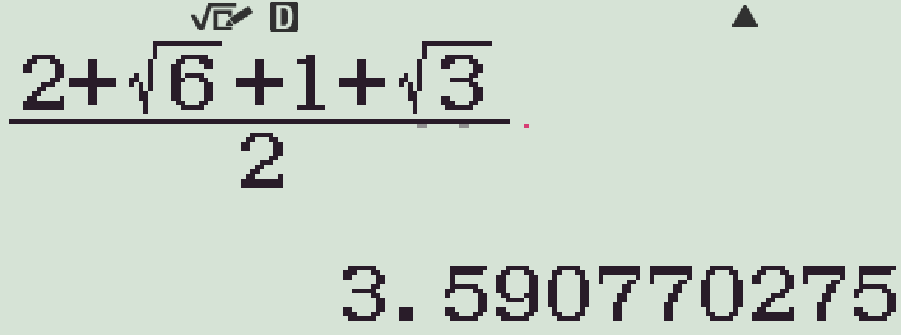
- Dùng công thức Heron tính diện tích:
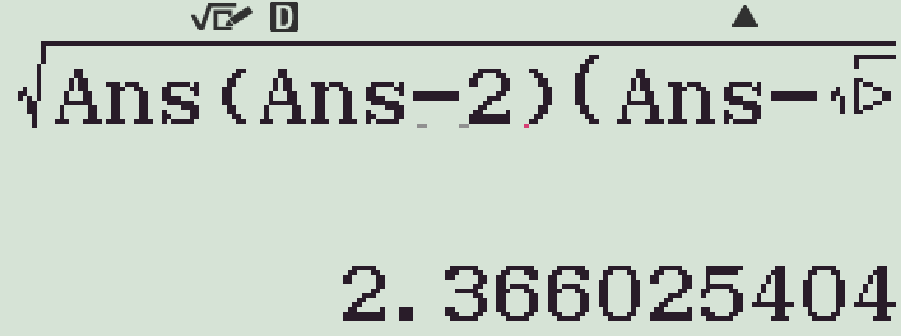
- Tính bán kính đường tròn ngoại tiếp:
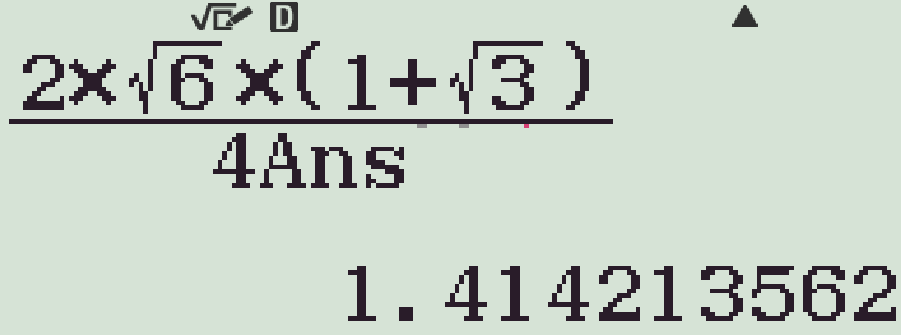
Chọn phương án C.
\(\begin{align*}\text{Ta có }\cos B&=\dfrac{a^2+c^2-b^2}{2ac}\\
&=\dfrac{2^2+\left(1+\sqrt{3}\right)^2-\left(\sqrt{6}\right)^2}{2\cdot2\left(1+\sqrt{3}\right)}\\
=\dfrac{1}{2}.\end{align*}\)
Suy ra \(\widehat{B}=60^\circ\).
Theo định lý sin ta được $$R=\dfrac{b}{2\sin B}=\dfrac{\sqrt{6}}{2\sin60^\circ}=\sqrt{2}.$$
