Ngân hàng bài tập
A
Cho tam giác \(ABC\) vuông cân tại \(A\) với \(AB=a\). Tính \(\left|\overrightarrow{AB}+\overrightarrow{AC}\right|\).
| \(\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=a\sqrt{2}\) | |
| \(\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=\dfrac{a\sqrt{2}}{2}\) | |
| \(\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=2a\) | |
| \(\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=a\) |
1 lời giải
Chọn phương án A.
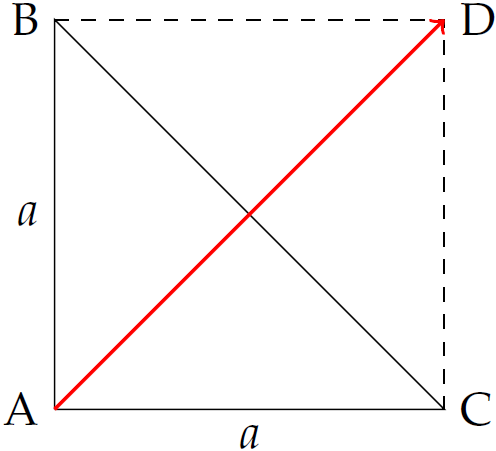
Gọi \(D\) là đỉnh thứ tư của hình bình hành \(ABDC\).
Vì \(AB=AC\) và \(\widehat{A}=90^\circ\) nên \(ABDC\) là hình vuông.
Theo quy tắc hình bình hành ta có \(\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AD}\).
Suy ra \(\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=\left|\overrightarrow{AD}\right|=a\sqrt{2}\).