Cho hai lực \(\overrightarrow{F_1}\) và \(\overrightarrow{F_2}\) có cùng điểm đặt tại \(O\). Biết \(\overrightarrow{F_1}\) và \(\overrightarrow{F_2}\) đều có cường độ là \(100\)N, góc hợp bởi \(\overrightarrow{F_1}\) và \(\overrightarrow{F_2}\) là \(120^\circ\). Cường độ lực tổng hợp của chúng là
| \(200\)N | |
| \(50\sqrt{3}\)N | |
| \(100\sqrt{3}\)N | |
| \(100\)N |
Chọn phương án D.
Giả sử \(\overrightarrow{F_1}=\overrightarrow{OA}\), \(\overrightarrow{F_2}=\overrightarrow{OB}\).
Gọi \(C\) là đỉnh thứ tư của hình bình hành \(OACB\) ta có $$\overrightarrow{F_1}+\overrightarrow{F_2}=\overrightarrow{OA}+\overrightarrow{OB}=\overrightarrow{OC}$$
Vì \(OA=OB=100\) nên \(OACB\) là hình thoi.
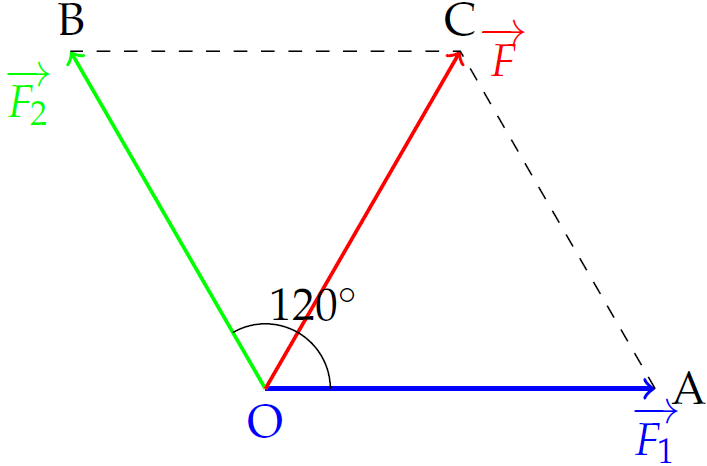
Mặt khác, vì \(\widehat{AOB}=\left(\overrightarrow{F_1},\overrightarrow{F_2}\right)=120^\circ\) nên suy ra \(\widehat{OAC}=60^\circ\).
Vậy tam giác \(OAC\) đều.
Suy ra \(\left|\overrightarrow{F_1}+\overrightarrow{F_2}\right|=\left|\overrightarrow{OC}\right|=OC=100\)N.
