Ngân hàng bài tập
S
Cho hai lực \(\overrightarrow{F_1}=\overrightarrow{MA}\) và \(\overrightarrow{F_2}=\overrightarrow{MB}\) cùng tác động vào một vật tại điểm \(M\). Cường độ hai lực \(\overrightarrow{F_1}\) và \(\overrightarrow{F_2}\) lần lượt là \(300\)N và \(400\)N, góc \(\widehat{AMB}=90^\circ\). Tính cường độ lực tổng hợp tác động vào vật.
| \(0\) | |
| \(700\) | |
| \(100\) | |
| \(500\) |
1 lời giải
Chọn phương án D.
Gọi \(C\) là đỉnh thứ tư của hình bình hành \(MACB\) ta có $$\overrightarrow{F_1}+\overrightarrow{F_2}=\overrightarrow{MA}+\overrightarrow{MB}=\overrightarrow{MC}.$$
Vì \(\widehat{AMB}=90^\circ\) nên \(MACB\) là hình chữ nhật.
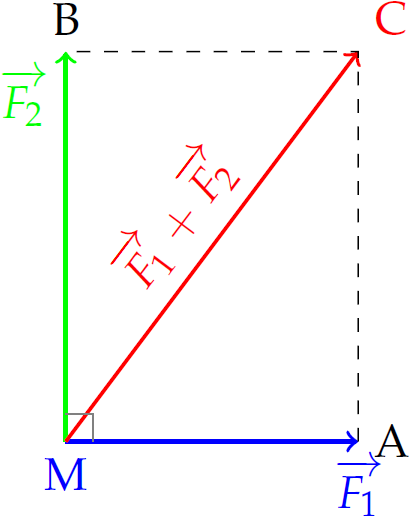
Suy ra \(\left|\overrightarrow{F_1}+\overrightarrow{F_2}\right|=MC=\sqrt{300^2+400^2}=500\)N.
