Cho ba lực \(\overrightarrow{F_1}=\overrightarrow{MA}\), \(\overrightarrow{F_2}=\overrightarrow{MB}\) và \(\overrightarrow{F_3}=\overrightarrow{MC}\) cùng tác động vào một vật tại điểm \(M\) và vật đứng yên. Biết rằng \(\overrightarrow{F_1},\,\overrightarrow{F_2}\) đều có cường độ lực là \(60\)N, và chúng vuông góc với nhau. Tính cường độ lực \(\overrightarrow{F_3}\).
| \(84,58\)N | |
| \(84,86\)N | |
| \(84,85\)N | |
| \(120\)N |
Chọn phương án C.
Gọi \(D\) là đỉnh thứ tư của hình bình hành \(MADB\) ta có $$\overrightarrow{F_1}+\overrightarrow{F_2}=\overrightarrow{MA}+\overrightarrow{MB}=\overrightarrow{MD}$$
Vì \(MA=MB=60\) và \(\widehat{AMB}=90^\circ\) nên \(MADB\) là hình vuông.
Suy ra \(MD=60\sqrt{2}\).
Khi đó \(\overrightarrow{F_3}=-\left(\overrightarrow{F_1}+\overrightarrow{F_2}\right)=-\overrightarrow{MD}\).
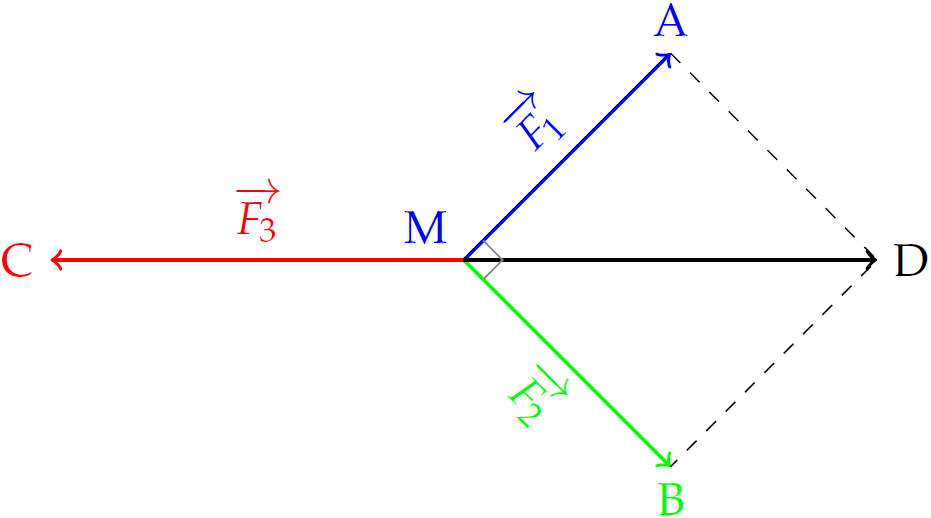
Vậy \(\left|\overrightarrow{F_3}\right|=\left|-\overrightarrow{OD}\right|=OD=60\sqrt{2}\approx84,85\)N.
