Ngân hàng bài tập
A
Cho hình thoi \(ABCD\) có \(AC=2a\) và \(BD=a\). Tính \(\left|\overrightarrow{AC}+\overrightarrow{BD}\right|\).
| \(\left|\overrightarrow{AC}+\overrightarrow{BD}\right|=3a\) | |
| \(\left|\overrightarrow{AC}+\overrightarrow{BD}\right|=a\sqrt{3}\) | |
| \(\left|\overrightarrow{AC}+\overrightarrow{BD}\right|=a\sqrt{5}\) | |
| \(\left|\overrightarrow{AC}+\overrightarrow{BD}\right|=5a\) |
1 lời giải
Chọn phương án C.
Gọi \(O\) là giao điểm của \(AC\) và \(BD\), \(M\) là trung điểm cạnh \(CD\). Ta có $$\begin{aligned}
\overrightarrow{AC}+\overrightarrow{BD}&=2\overrightarrow{OC}+2\overrightarrow{OD}\\
&=2\left(\overrightarrow{OC}+\overrightarrow{OD}\right)\\
&=2\cdot2\overrightarrow{OM}=4\overrightarrow{OM}.
\end{aligned}$$Vậy \(\left|\overrightarrow{AC}+\overrightarrow{BD}\right|=4OM\).
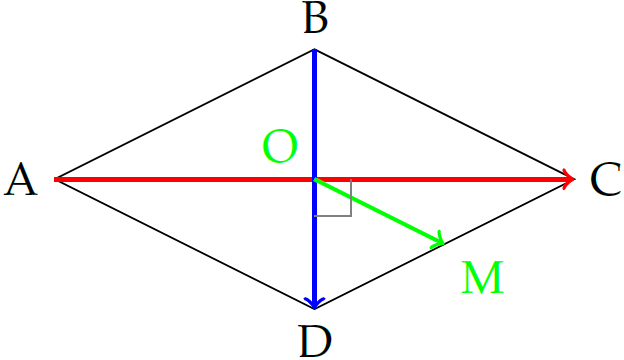
Xét tam giác vuông \(OCD\) ta có:
- \(CD\) là cạnh huyền nên $$\begin{aligned}CD&=\sqrt{OC^2+OD^2}=\sqrt{a^2+\left(\dfrac{a}{2}\right)^2}\\ &=\dfrac{a\sqrt{5}}{2}.\end{aligned}$$
- \(OM\) là đường trung tuyến ứng với cạnh huyền \(CD\) nên \(OM=\dfrac{CD}{2}=\dfrac{a\sqrt{5}}{4}\).
Vậy \(\left|\overrightarrow{AC}+\overrightarrow{BD}\right|=4\cdot\dfrac{a\sqrt{5}}{4}=a\sqrt{5}\).
