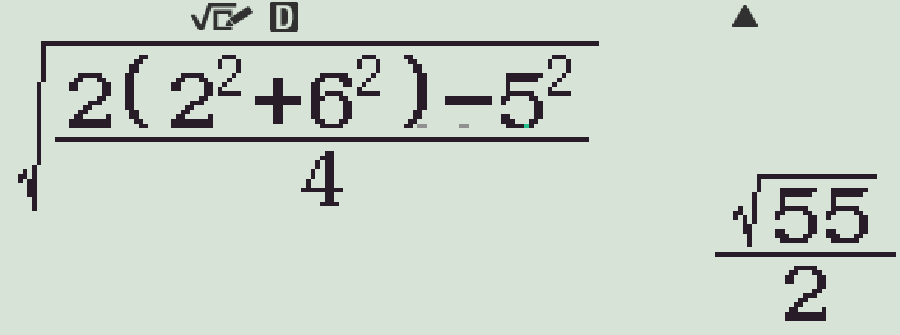Ngân hàng bài tập
C
Cho tam giác \(ABC\) có độ dài ba cạnh là \(AB=2\), \(BC=5\), \(CA=6\). Tính độ dài đường trung tuyến \(AM\).
| \(\dfrac{\sqrt{15}}{2}\) | |
| \(\dfrac{\sqrt{55}}{2}\) | |
| \(\dfrac{\sqrt{110}}{2}\) | |
| \(\sqrt{55}\) |
1 lời giải
Chọn phương án B.
\(\begin{align*}\text{Ta có }AM^2&=\dfrac{2\left(AB^2+AC^2\right)-BC^2}{4}\\
&=\dfrac{55}{4}.\end{align*}\)
Suy ra \(AM=\dfrac{\sqrt{55}}{2}\).