Cho tam giác \(ABC\) đều, cạnh \(a\), có \(I,\,J,\,K\) lần lượt là trung điểm các cạnh \(BC,\,CA,\,AB\). Tính giá trị của $$\left|\overrightarrow{AI}+\overrightarrow{BJ}+\overrightarrow{CK}\right|.$$
| \(3a\) | |
| \(\dfrac{3a\sqrt{3}}{2}\) | |
| \(0\) | |
| \(\dfrac{a\sqrt{3}}{2}\) |
Chọn phương án C.
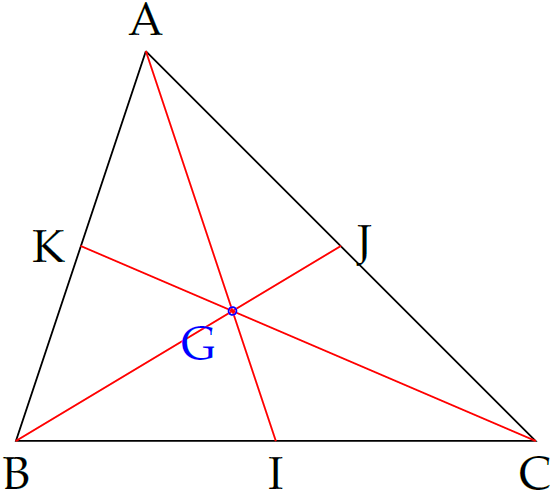
Theo đề, ta có các đường trung tuyến \(AI,\,BJ,\,CK\).
Gọi \(G\) là trọng tâm của tam giác \(ABC\), ta có $$\begin{cases}
\overrightarrow{AI}=-\dfrac{3}{2}\overrightarrow{GA}\\
\overrightarrow{BJ}=-\dfrac{3}{2}\overrightarrow{GB}\\
\overrightarrow{CK}=-\dfrac{3}{2}\overrightarrow{GC}
\end{cases}$$
Khi đó, $$\begin{aligned}
\overrightarrow{AI}+\overrightarrow{BJ}+\overrightarrow{CK}&=-\dfrac{3}{2}\left(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}\right)\\
&=-\dfrac{3}{2}\cdot\vec{0}=\vec{0}.
\end{aligned}$$
Vậy \(\left|\overrightarrow{AI}+\overrightarrow{BJ}+\overrightarrow{CK}\right|=0\).
