Ngân hàng bài tập
A
Cho hình vuông \(ABCD\) cạnh \(a\). Khi đó \(\left|\overrightarrow{AB}+\overrightarrow{AC}\right|\) bằng
| \(a\sqrt{5}\) | |
| \(\dfrac{a\sqrt{5}}{2}\) | |
| \(2a\) | |
| \(a\sqrt{3}\) |
1 lời giải
Chọn phương án A.
Gọi \(M\) là trung điểm cạnh \(BC\), ta có \(\overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AM}\) (1).
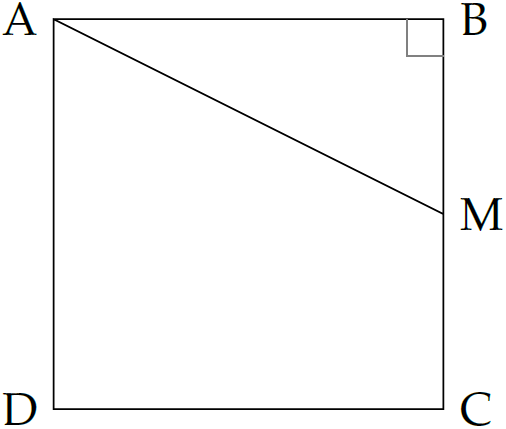
Xét tam giác vuông \(ABM\) ta có $$\begin{aligned}AM&=\sqrt{AB^2+BM^2}=\sqrt{a^2+\left(\dfrac{a}{2}\right)^2}\\
&=\dfrac{a\sqrt{5}}{2}\,\,(2).\end{aligned}$$
Từ (1) và (2) suy ra \(\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=2AM=a\sqrt{5}\).
