Ngân hàng bài tập
A
Trong không gian \(Oxyz\), cho hình hộp \(ABCD.EFGH\) có \(A(1;1;-6)\), \(B(0;0;-2)\), \(C(-5;1;2)\), \(H(2;1;-1)\). Tính thể tích của khối hộp đã cho.
| \(V=36\) | |
| \(V=38\) | |
| \(V=\dfrac{19}{3}\) | |
| \(V=42\) |
1 lời giải
Chọn phương án B.
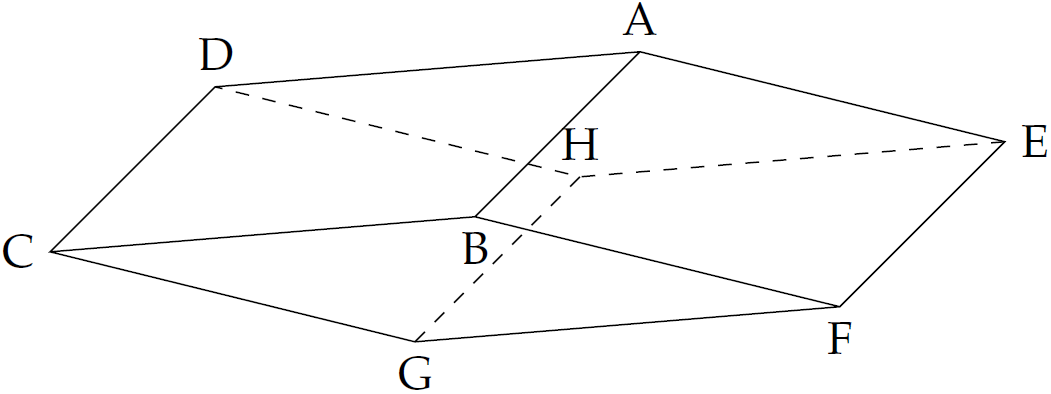
Vì \(ABCD\) là hình bình hành nên $$\begin{cases}
x_D=x_A+x_C-x_B=-4\\
y_D=y_A+y_C-y_B=2\\
z_D=z_A+z_C-z_B=-2\\
\end{cases}$$
Ta có \(\overrightarrow{DA}=(5;-1;-4)\), \(\overrightarrow{DC}=(-1;-1;4)\), \(\overrightarrow{DH}=(6;-1;1)\).
Khi đó, \(\left[\overrightarrow{DA},\overrightarrow{DC}\right]=(-8;-16;-6)\).
Suy ra \(V_{ABCD.EFGH}=\left|\left[\overrightarrow{DA},\overrightarrow{DC}\right]\cdot\overrightarrow{DH}\right|=38\).
