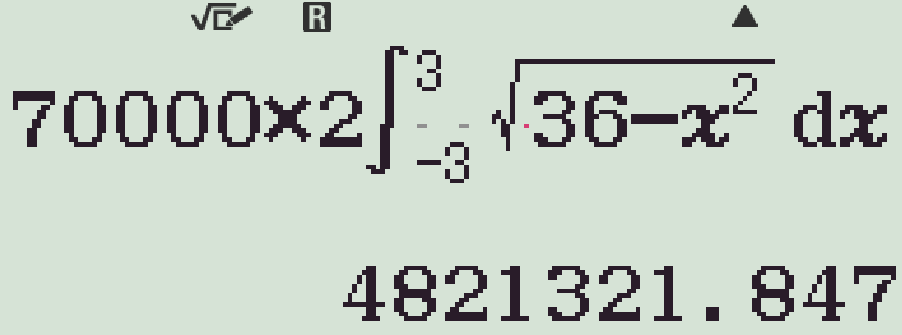Một mảnh vườn hình tròn tâm \(O\) bán kính \(6\)m. Người ta cần trồng cây trên dải đất rộng \(6\)m nhận \(O\) làm tâm đối xứng, biết kinh phí trồng cây là \(70000\) đồng/m\(^2\).
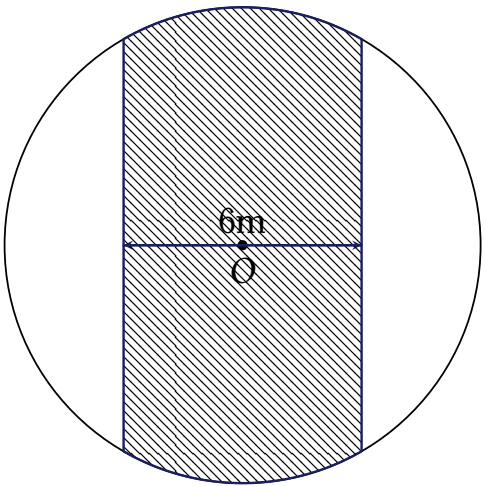
Hỏi cần bao nhiêu tiền để trồng cây trên dải đất đó?
| \(8.412.322\) đồng | |
| \(4.821.322\) đồng | |
| \(3.142.232\) đồng | |
| \(4.821.232\) đồng |
Chọn phương án B.
Đặt hệ trục \(Oxy\) như hình vẽ.
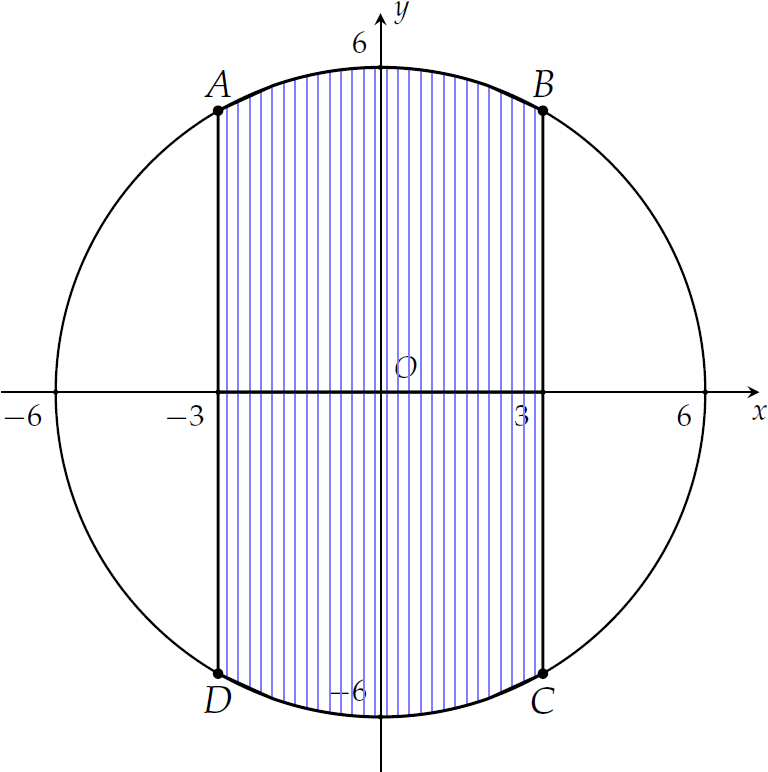
Ta có phương trình đường tròn $$x^2+y^2=36\Leftrightarrow y=\pm\sqrt{36-x^2}.$$
Diện tích phần trồng cây $$\begin{aligned}S&=\displaystyle\int\limits_{-3}^3\left[\sqrt{36-x^2}-\left(-\sqrt{36-x^2}\right)\right]\mathrm{\,d}x\\
&=2\int\limits_{-3}^3\sqrt{36-x^2}\mathrm{\,d}x.\end{aligned}$$
\(\Rightarrow{\rm{d}}x=6\cos t\mathrm{\,d}t\).
Đổi cận: \(\begin{cases}
x=-3\Rightarrow t=-\dfrac{\pi}{6}\\ x=3\Rightarrow t=\dfrac{\pi}{6}.
\end{cases}\)
Khi đó:
$$\begin{eqnarray*}
&S&=2\displaystyle\int\limits_{-\frac{\pi}{6}}^{\frac{\pi}{6}}\sqrt{36-36\sin^2t}\cdot 6\cos t\mathrm{\,d}t\\
&&=72\displaystyle\int\limits_{-\frac{\pi}{6}}^{\frac{\pi}{6}}\cos^2t\mathrm{\,d}t\\
&&=36\displaystyle\int\limits_{-\frac{\pi}{6}}^{\frac{\pi}{6}}(1+\cos 2t)\mathrm{\,d}t\\
&&=\left. 36\left(t+\dfrac{1}{2}\sin 2t\right)\right|_{\frac{\pi}{6}}^{\frac{\pi}{6}}\\
&&=12\pi+18\sqrt 3.
\end{eqnarray*}$$
Vậy số tiền cần để trồng cây là $$70000\cdot S\approx 4.821.322\,\text{đồng.}$$