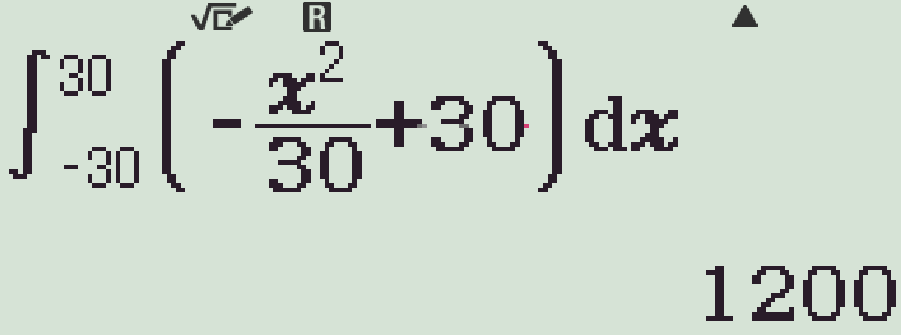Ngân hàng bài tập
S
Bạn An cần mua một chiếc gương có viền là đường parabol bậc hai (như hình vẽ).
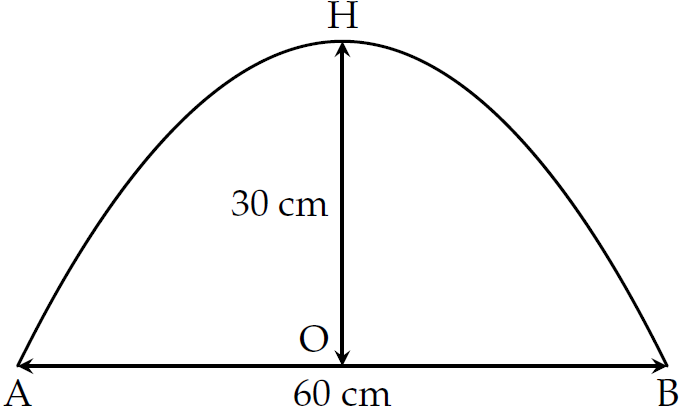
Biết rằng đoạn \(AB=60\) cm, \(OH=30\) cm. Diện tích của chiếc gương bạn An mua là
| \(1000\) cm\(^2\) | |
| \(1400\) cm\(^2\) | |
| \(1200\) cm\(^2\) | |
| \(900\) cm\(^2\) |
1 lời giải
Chọn phương án C.
Xét hệ trục tọa độ \(Oxy\), sao cho gốc \(O\) trùng với điểm \(O\), trục \(Ox\) trùng với tia \(OB\), trục \(Oy\) trùng với tia \(OH\).
Khi đó \(A(-30;0)\), \(B(30;0)\), \(H(0;30)\).
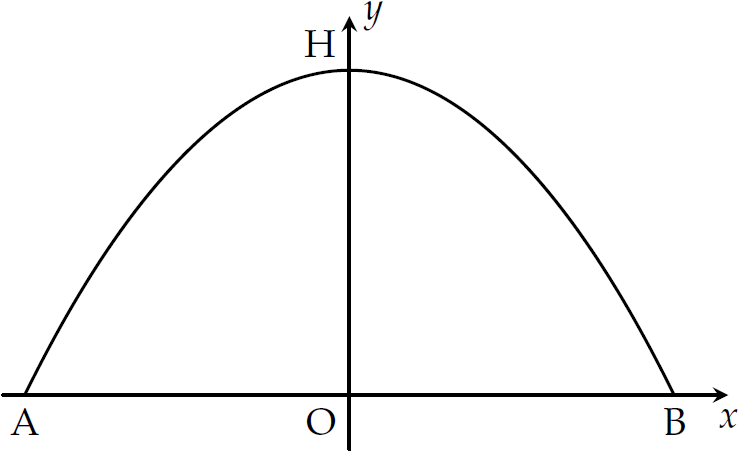
Phương trình Parabol đi qua \(A\), \(H\), \(B\) có dạng \(y=ax^2+b\quad(P)\).
- \(H\in (P)\Rightarrow 30=b\)
- \(B\in (P)\Rightarrow 0=a\cdot 30^2+30\Rightarrow a =-\dfrac{1}{30}\)
Vậy \((P)\colon y=-\dfrac{x^2}{30}+30\).
Diện tích của chiếc gương là
$$\begin{aligned}\displaystyle\int\limits_{-30}^{30}\left(-\dfrac{x^2}{30}+30\right)\mathrm{\,d}x&=\left(-\dfrac{x^3}{90}+30x\right)\bigg|_{-30}^{30}\\
&=1200\,(\text{cm}^2).\end{aligned}$$